共用方式為

轉換 (Direct3D 9)

  • 發行項

在 Direct3D 中，轉換引擎負責將幾何推入固定函式幾何管線。 它在世界中尋找模型和檢視器，將頂點投影在螢幕上顯示，並將頂點裁剪至檢視區。 轉換引擎也會執行光線計算，以判斷每個頂點上的擴散和反射元件。

幾何管線使用頂點做為輸入。 轉換引擎將世界、檢視和影轉換套用至頂點，剪輯結果，然後將所有項目傳遞至轉譯器。

在管線的開頭，模型頂點的宣告是相對於區域座標系統。 這是區域原點和方向。 這個座標方向通常稱為模型空間，而個別座標稱為模型座標。

幾何管線的第一階段會將模型的頂點從其區域座標系統轉換成場景中所有物件所使用的座標系統。 重新導向頂點的程式稱為世界轉換。 這個新方向通常稱為世界空間，而世界空間中的每個頂點都會使用全局座標來宣告。

在下一個階段，描述您 3D 世界的頂點是相對於相機定向的。 也就是說，您的應用程式會為場景選擇一個檢視點，而世界空間座標會重新放置並旋轉在相機的檢視周圍，並將世界空間轉換成相機空間。 這是檢視轉換。

下一個階段是投影轉換。 在管線的這個部分中，物件通常會以與其與檢視器之間的距離來縮放，以便讓場景的深度錯覺;close 物件會變成大於遠距物件，依此類加。 為了簡化，本文件將是投影轉換後頂點的存在空間稱為投影空間。 一些圖形書籍可能將投影空間稱為透視後同質空間。 並非所有投影轉換都會將場景中的物件大小縮放。 這類投影有時稱為仿射或正交投影。

在管線的最後一部分，將不會顯示在螢幕上的任何頂點移除，以便轉譯器不會花時間計算永遠不會看到之項目的色彩和陰影。 此程序稱為裁剪。 裁剪之後，剩餘頂點依據檢視區參數縮放，而且轉換成螢幕座標。 結果頂點 (當場景點陣化時會顯示在螢幕上) 存在於螢幕空間。

轉換用於將物件幾何從某個座標轉換到另一個座標。 Direct3D 使用矩陣執行 3D 轉換。 本節說明矩陣如何建立 3D 轉換、描述轉換的一些常見用途，以及詳細說明如何結合矩陣來產生包含多個轉換的單一矩陣。

矩陣轉換

在與 3D 圖形搭配運作的應用程式，您可以使用幾何轉換，執行下列動作：

  • 表示某物件相對於另一個物件的位置。
  • 旋轉和調整物件大小。
  • 變更檢視位置、方向及透視圖。

使用 4x4 矩陣，您可以將任何點 (x,y,z) 轉換成另一個點 (x', y', z')，如下面方程式中顯示。

將任何點轉換成另一個點的方程式

在 (x, y, z) 和矩陣執行下列方程式以產生點 (x', y', z')。

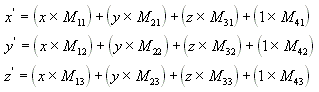
新點的方程式

最常見的轉換是轉移、旋轉和縮放比例。 您可以將產生這些效果的矩陣結合成單一矩陣，一次計算幾個轉換。 例如，您可以建立單一矩陣以轉移並旋轉一系列的點。

矩陣依列-欄順序寫入。 沿著每個軸稱平均縮放頂點 (稱為統一縮放) 的矩陣，由下列使用數學符號的矩陣表示。

統一縮放矩陣的方程式

在 C++ 中，Direct3D 會使用 D3DMATRIX 結構，將矩陣宣告為二維陣列。 下列範例示範如何初始化 D3DMATRIX 結構，以做為統一縮放矩陣。

// In this example, s is a variable of type float.

D3DMATRIX scale = {
    s,               0.0f,            0.0f,            0.0f,
    0.0f,            s,               0.0f,            0.0f,
    0.0f,            0.0f,            s,               0.0f,
    0.0f,            0.0f,            0.0f,            1.0f
};

Translate

下面方程式將點 (x, y, z) 轉移到新點 (x', y', z')。

新點轉移矩陣的方程式

您可以在 C++ 中手動建立轉移矩陣。 下列範例程式碼示範如何建立矩陣以轉移頂點的功能。

D3DXMATRIX Translate(const float dx, const float dy, const float dz) {
    D3DXMATRIX ret;

    D3DXMatrixIdentity(&ret);
    ret(3, 0) = dx;
    ret(3, 1) = dy;
    ret(3, 2) = dz;
    return ret;
}    // End of Translate

為了方便起見，D3DX 公用程式程式庫會提供 D3DXMatrixTranslation 函式 。

調整

下面方程式以 x、y 與 z 方向的任意值，將點 (x, y, z) 縮放成新點 (x', y', z')。

新點縮放矩陣的方程式

Rotate

這裡描述的轉換適用於左手座標系統，因此可能不同於您在其他地方看到的轉移矩陣。

下面方程式圍繞 x 軸旋轉點 (x, y, z)，產生新點 (x', y', z')。

新點 x 旋轉矩陣的方程式

下面方程式圍繞 y 軸旋轉點。

新點 y 旋轉矩陣的方程式

下面方程式圍繞 z 軸旋轉點。

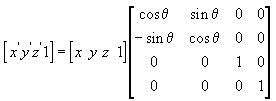
新點 z 旋轉矩陣的方程式

在這些範例矩陣，希臘字母 theta 表示旋轉角度 (以弧度為單位)。 沿著旋轉軸向原點方向看時，角度是順時針方向測量。

在 C++ 應用程式中，使用 D3DXMatrixRotationX、 D3DXMatrixRotationY和 D3DXMatrixRotationZ 函式所提供的 D3DXMatrixRotationZ 函式來建立旋轉矩陣。 以下是 D3DXMatrixRotationX 函式的程式碼。

D3DXMATRIX* WINAPI D3DXMatrixRotationX
    ( D3DXMATRIX *pOut, float angle )
{
#if DBG
    if(!pOut)
        return NULL;
#endif

    float sin, cos;
    sincosf(angle, &sin, &cos);  // Determine sin and cos of angle

    pOut->_11 = 1.0f; pOut->_12 =  0.0f;   pOut->_13 = 0.0f; pOut->_14 = 0.0f;
    pOut->_21 = 0.0f; pOut->_22 =  cos;    pOut->_23 = sin;  pOut->_24 = 0.0f;
    pOut->_31 = 0.0f; pOut->_32 = -sin;    pOut->_33 = cos;  pOut->_34 = 0.0f;
    pOut->_41 = 0.0f; pOut->_42 =  0.0f;   pOut->_43 = 0.0f; pOut->_44 = 1.0f;

    return pOut;
}

串連矩陣

使用矩陣的一個優點是，您可以透過將矩陣相乘，組合兩個或更多矩陣的效果。 這表示，若要旋轉模型，然後將它轉移到特定位置，您不需要套用兩個矩陣。 而是，您將旋轉矩陣和轉移矩陣相乘，產生一個包含所有效果的複合矩陣。 這個程序，稱為矩陣串連，可以使用下面方程式撰寫。

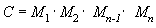
矩陣串連的方程式

在這個方程式中，C 是所建立的複合矩陣，而 M₁ 到 Mₙ 是個別矩陣。 在大部分案例中，只會串連兩個或三個矩陣，但沒有限制。

使用 D3DXMatrixMultiply 函式來執行矩陣乘法。

執行矩陣乘法的順序非常重要。 上述公式反映矩陣串連的由左至右規則。 也就是，您用來建立複合矩陣之矩陣的可見效果是依由左至右的順序發生。 以下範例顯示一般世界矩陣。 想像您要為定型飛行器建立世界矩陣。 您可能會想要圍繞飛行器的中心 (模型空間的 y 軸) 來旋轉飛行器，並將它轉移到場景中的其他位置。 若要完成此效果，您首先建立旋轉矩陣，再將它乘以轉移矩陣，如下面方程式中顯示。

根據旋轉矩陣和轉移矩陣之旋轉的方程式

在這個公式中，Ry 是圍繞 y 軸之旋轉的矩陣，而 Tw 則是轉移到世界座標中的特定位置。

矩陣相乘的順序很重要，因為不像兩個純量數值相乘，矩陣乘法不具交換性。 依相反順序將矩陣相乘，有轉移飛行器到世界空間位置，然後圍繞世界原點旋轉的視覺效果。

無論您建立何種矩陣類型，請記住由左至右規則，以確定您達到預期的效果。

快速入門