O qubit na computação quântica
Assim como os bits são o objeto fundamental das informações na computação clássica, qubits (bits quânticos) são o objeto fundamental das informações na computação quântica. Para entender essa correspondência, este artigo analisa o exemplo mais simples: um qubit único.
Representando um qubit
Embora um bit, ou dígito binário, possa ter valor $0$ ou $1$, um qubit pode ter um valor que seja $0$, $1$ ou uma sobreposição quântica de $0$ e $1$.
O estado de um qubit único pode ser descrito por um vetor de coluna bidimensional da norma de unidade, ou seja, a magnitude quadrada de suas entradas deve somar $1$. Esse vetor, chamado de vetor de estado quântico, contém todas as informações necessárias para descrever o sistema quântico de qubit, assim como um único bit contém todas as informações necessárias para descrever o estado de uma variável binária. Para obter os conceitos básicos de vetores e matrizes na computação quântica, consulte Vetor e matrizes.
Qualquer vetor de coluna bidimensional de números reais ou complexos com a norma $1$ representa um possível estado quântico mantido por um qubit. Assim, $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ representa um estado qubit se $\alpha$ e $\beta$ são números complexos que satisfazem $|\alpha|^2 + |\beta|^2 = 1$.
Alguns exemplos de vetores de estado quântico válidos que representam qubits são $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ e $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Esses dois vetores formam uma base para o espaço vetorial que descreve o estado do qubit. Isso significa que qualquer vetor de estado quântico pode ser escrito como uma soma desses vetores de base. Especificamente, o vetor $\begin{bmatrix} x \\ y \end{bmatrix}$ pode ser gravado como $x \begin{bmatrix} 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Embora qualquer rotação desses vetores sirva como uma base perfeitamente válida para o qubit, escolhemos essa, chamando-a de base computacional.
Esses dois estados quânticos são usados para corresponder aos dois estados de um bit clássico, a saber, $0$ e $1$. A convenção padrão é escolher
$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}$$$$1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix},$$
embora a escolha oposta pudesse ser igualmente feita. Portanto, fora do número infinito de vetores de estado quântico de qubit único, apenas dois correspondem a estados de bits clássicos; todos os outros estados quânticos não.
Medindo um qubit
Agora que sabemos como representar um qubit, podemos obter alguma ideia sobre o que esses estados representam discutindo o conceito de medida. Uma medida corresponde à ideia informal de "olhar" um qubit, que reduz imediatamente o estado quântico a um dos dois estados clássicos $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ ou $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Quando um qubit fornecido pelo vetor de estado quântico $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ é medido, obtemos o resultado $0$ com a probabilidade $|\alpha|^2$ e o resultado $1$ com a probabilidade $|\beta|^2$. No resultado $0$, o novo estado do qubit é $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$; no resultado $1$, seu estado é $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Observe que essas probabilidades somam até $1$ devido à condição de normalização $|\alpha|^2 + |\beta|^2 = 1$.
As propriedades de medida também significam que o sinal geral do vetor de estado quântico é irrelevante. Negar um vetor é equivalente a $\alpha\rightarrow -\alpha$ e $\beta\rightarrow -\beta$. Como a probabilidade de medir $0$ e $1$ depende da magnitude quadrada dos termos, inserir tais sinais não altera as probabilidades. Essas fases costumam ser chamadas de "fases globais" e, mais geralmente, podem estar no formato $e^{i \phi}$ em vez de apenas $\pm 1$.
Uma propriedade final importante da medição é que ela não necessariamente danifica todos os vetores de estado quântico. Se começarmos com um qubit no estado $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$, que corresponde ao estado clássico $0$, medir esse estado sempre produzirá o resultado $0$ e deixará o estado quântico inalterado. Nesse sentido, se tivermos apenas bits clássicos (por exemplo, qubits que sejam $\begin{bmatrix}1 \\ 0 \end{bmatrix}$ ou $\begin{bmatrix}0 \\ 1 \end{bmatrix}$), a medição não danificará o sistema. Isso significa que podemos replicar dados clássicos e manipulá-los em um computador quântico da mesma forma que em um computador clássico. No entanto, a capacidade de armazenar informações em ambos os estados de uma vez é o que eleva a computação quântica para além do que é possível de forma clássica e diminui ainda mais a capacidade de copiar dados quânticos indiscriminadamente, consulte também o teorema da não clonagem.
Visualizando qubits e transformações usando a esfera de Bloch
Qubits também podem ser ilustrados em $3$D usando a representação de esfera de Bloch. A esfera de Bloch fornece uma maneira de descrever um estado quântico de qubit único (que é um vetor complexo bidimensional) como vetor de valor real tridimensional. Isso é importante porque permite visualizar estados de qubit único e, assim, desenvolver um raciocínio que pode ser inestimável na compreensão de estados de vários qubits (para os quais infelizmente a representação de esfera de Bloch falha). A esfera de Bloch pode ser visualizada da seguinte maneira:
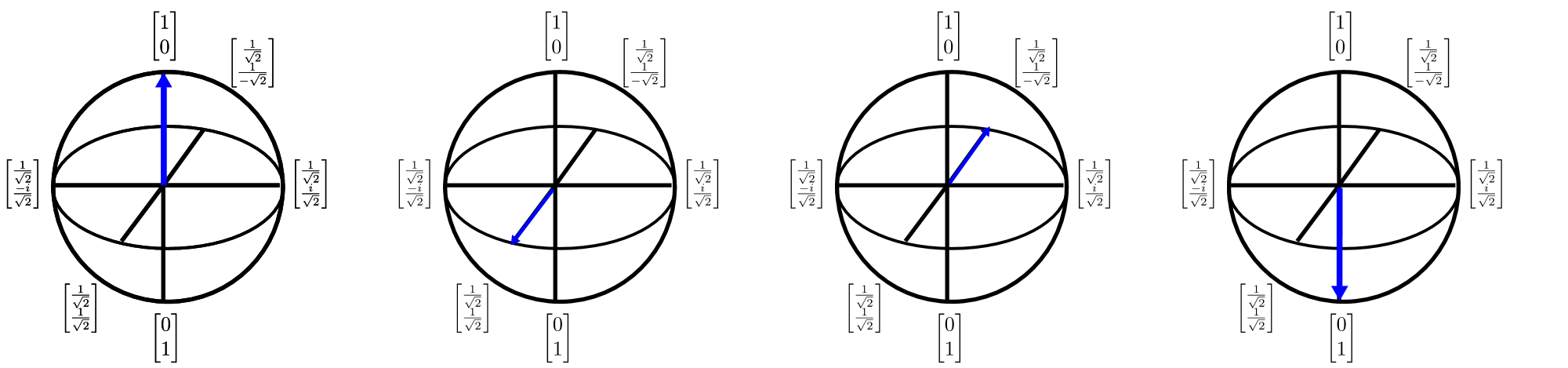
As setas neste diagrama mostram a direção em que o vetor de estado quântico está apontando e cada transformação da seta pode ser considerada como uma rotação de um dos eixos cardinal. Embora pensar em uma computação quântica como sequência de rotações seja uma ideia poderosa, é desafiador usar essa ideia para projetar e descrever algoritmos. Q# alivia esse problema fornecendo uma linguagem para descrever essas rotações.
Operações de qubit único
Os computadores quânticos processam dados aplicando um conjunto universal de portões quânticos que podem emular qualquer rotação do vetor de estado quântico. Essa noção de universalidade é semelhante à noção de universalidade da computação tradicional (por exemplo, clássica), em que um conjunto de portões é considerado universal se cada transformação dos bits de entrada puder ser executada usando um circuito de comprimento finito. Na computação quântica, as transformações válidas que temos permissão para executar em um qubit são transformações e medição de unitários. A operação adjoin ou a transposição de conjugado complexo é de importância crucial para a computação quântica porque é necessária para inverter as transformações quânticas.
As operações de qubit único ou portas quânticas de qubit único podem ser classificadas em duas categorias: portas de Clifford e portas não Clifford. Os portões não Clifford consistem apenas no $portão T$ (também conhecido como $portão \pi/8$ ).
$ T=\begin{bmatrix} 1 & 0 \ 0 & e^{i\pi/4}\end{bmatrix}. $$
O conjunto padrão de portas Clifford de qubit único, incluído por padrão no Q#, inclui
$ H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \ 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 \ 0 & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 &1 \ 1& 0 \end{bmatrix}= HT^4H, $
$ Y =\begin{bmatrix} 0 & -i \ i & 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1&0\ 0&-1 \end{bmatrix}=T^4. $$
Aqui, as operações $X$, $Y$ e $Z$ são usadas especialmente de forma frequente e são nomeadas como operadores Pauli em homenagem a seu criador Wolfgang Pauli. Junto com o portão não Clifford (o portão $T$), essas operações podem ser compostas para aproximar qualquer transformação de unitários em um qubit único.
Embora o anterior constitua os portões primitivos mais populares para descrever as operações no nível lógico da pilha (considere o nível lógico como o nível do algoritmo quântico), geralmente é conveniente considerar menos operações básicas no nível de algoritmo, por exemplo, operações mais próximas de um nível de descrição de função. Felizmente, Q# também tem métodos disponíveis para a implementação de unidades de nível superior, que, por sua vez, permitem que algoritmos de alto nível sejam implementados sem decompor explicitamente tudo em portões Clifford e $T$.
O mais simples desses primitivos é a rotação de qubit único. Três rotações de qubit único normalmente são consideradas: $R_x$, $R_y$ e $R_z$. Para visualizar a ação da rotação $R_x(\theta)$, por exemplo, imagine apontar o polegar direito ao longo da direção do eixo $x$ da esfera de Bloch e girar o vetor com sua mão em um ângulo de $\teta/2$ radianos. Esse fator confuso de $2$ é devido ao fato de que os vetores ortogonais estão separados por$180^\circs$ quando plotados na esfera de Bloch, mas estão, na verdade, separados por $90^\circ$ graus geométricos. As matrizes de unitários correspondentes são:
$ \begin{align*}&R_z(\theta) = e^{-i\theta Z/2}=\begin{bmatrix} e^{-i\theta/2}& 0\\ 0& e^{i\theta/2}\end{bmatrix}, \\&R_x(\theta) = e^{-i\theta X/2}= HR_z(\theta)H =\begin{bmatrix} \cos(\theta/2) & -i\sin(\theta/2)\\ -i\sin(\theta/2) & \cos(\theta/2) \end{bmatrix}, \\&R_y(\theta) = e^{-i\theta Y/2}= SHR_z(\theta)HS^\dagger=\begin{bmatrix} \cos(\theta/2) & -\sin(\theta/2)\\ \sin(\theta/2) & \cos(\theta/2) \end{bmatrix}. \end{align*}$
Assim como as três rotações podem ser combinadas para executar uma rotação arbitrária em três dimensões, pode ser visto na representação da esfera de Bloch que qualquer matriz de unitários também pode ser gravada como sequência de três rotações. Especificamente, para cada matriz de unitários $U$, existe $\alpha,\beta,\gamma,\delta$ de forma que $U= e^{i\alpha} R_x(\beta)R_z(\gamma)R_x(\delta)$. Portanto $R_z(\theta)$ e $H$ também formam um conjunto de portões universal, embora não seja um conjunto discreto, porque $\theta$ pode usar qualquer valor. Por esse motivo, e devido a aplicativos na simulação quântica, esses portões contínuos são cruciais para a computação quântica, especialmente no nível de design do algoritmo quântico. Para obter a implementação de hardware tolerante a falhas, elas serão eventualmente compiladas em sequências de portão discretas que se aproximam bastante dessas rotações.