Regras de diagrama de circuito quântico
Às vezes, os algoritmos quânticos são mais fáceis de entender em um diagrama de circuito do que na representação matricial escrita equivalente. Este artigo explica como ler diagramas de circuitos quânticos e suas convenções.
Para obter mais informações, consulte Como visualizar diagramas de circuitos quânticos.
Lendo diagramas de circuitos quânticos
Em um circuito quântico, o tempo flui da esquerda para a direita. As portas quânticas são ordenadas em ordem cronológica com a porta mais à esquerda como a porta aplicada pela primeira vez ao qubits.
Tome o seguinte diagrama de circuito quântico como exemplo:
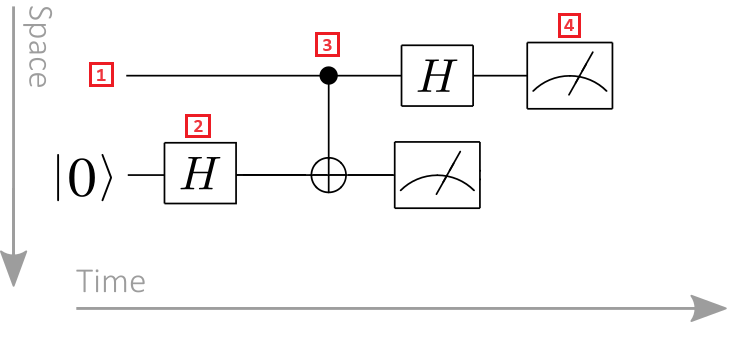
- Registro de qubit: os registros de qubit são exibidos como linhas horizontais, com cada linha representando um qubit. A linha superior é o registro de qubit rotulado como 0, a segunda linha é o registro de qubit rotulado como 1 e assim por diante.
- Porta quântica: As operações quânticas são representadas por portas quânticas. O termo porta quântica é análogo a portas lógicas clássicas. As portas que atuam em um ou mais registros de qubit são indicadas como caixas. Neste exemplo, o símbolo representa uma operação de Hadamard.
- Portão controlado: os portões controlados atuam em dois ou mais qubits. Neste exemplo, o símbolo representa uma porta CNOT. O círculo preto representa o qubit de controle e a cruz dentro de um círculo representa o target qubit.
- Operação de medição: O símbolo do medidor representa uma operação de medição. A operação de medição usa um registro de qubit como entrada e gera informações clássicas.
Aplicando portas quânticas
Como o tempo flui da esquerda para a direita, a porta mais à esquerda é aplicada primeiro Por exemplo, a ação do circuito quântico a seguir é a matriz $unitária CBA$.
Observação
A multiplicação de matriz obedece à regra oposta: a matriz mais à direita é aplicada primeiro. Em diagramas de circuito quântico no entanto, a porta mais à esquerda é aplicada primeiro. Ás vezes essa diferença pode confundir, portanto, é importante observar essa diferença significativa entre notação algébrica linear e diagramas de circuito quântico.
Entradas e saídas de circuitos quântico
Em um diagrama de circuito quântico, os fios que entram em uma porta quântica representam os qubits que são inseridos na porta quântica e os fios que saem da porta quântica representam os qubits que são gerados pela porta quântica.
O número de entradas de uma porta quântica é igual ao número de saídas de uma porta quântica. Isso ocorre porque as operações quânticas são unitárias e, portanto, reversíveis. Se uma porta quântica tivesse mais saídas do que entradas, ela não seria reversível e, portanto, não seria unitária, o que é uma contradição.
Por esse motivo, qualquer caixa desenhada em um diagrama de circuito deve ter precisamente o mesmo número de fios inserindo-a e retirando-a.
Operações de vários qubits
Os diagramas de circuito qubit seguem regras semelhantes para os qubit únicos. Por exemplo, uma operação $unitária B$ de dois qubits pode ser definida como $(H S\otimes X),$ portanto, o circuito quântico equivalente é o seguinte:
Você também pode exibir a $B$ como se tivesse uma ação em um único registro de dois qubits em vez de dois registros de um qubit, dependendo do contexto no qual o circuito é usado.
Talvez a propriedade mais útil desses diagramas de circuito abstrato seja que eles permitem que algoritmos quânticos complexos sejam descritos em um alto nível sem precisar compilá-los em portas fundamentais. Isso significa que é possível intuir sobre o fluxo de dados de um grande algoritmo quântico sem a necessidade de entender todos os detalhes de como cada uma das sub-rotinas dentro do algoritmo funciona.
Portas controladas
Os portões controlados por quantum são portões de dois qubits que aplicam um qubit target único
Por exemplo, considere uma porta controlada quântica, denotada por $\Lambda(G)$, em que o valor de um único qubit controla a aplicação da operação $G$. A porta $\Lambdacontrolada (G)$ pode ser entendida observando o seguinte exemplo de uma entrada de estado do produto:
$$\Lambda(G) (\alpha\ket{{0} + \beta\ket{1}) \ket{\psi}=\alpha\ket{{0}\ket{\psi} + \beta\ket{{1} G\ket{\psi}$$
Ou seja, o portão controlado aplicará $G$ ao registro que contém $\psi$ se e somente se o qubit de controle usar o valor $1$. Em geral, essas operações controladas são descritas em diagramas de circuito pelo seguinte símbolo:
Aqui, o círculo preto indica o bit quântico no qual a porta é controlada e uma transmissão vertical denota o unitário que é aplicado quando o qubit de controle usa o valor $1$.
Para os casos especiais em $que G=X$ e $G=Z$, a seguinte notação é usada para descrever a versão controlada das portas (observe que a porta X controlada é a porta CNOT):
Q# fornece métodos para gerar automaticamente a versão controlada de uma operação, o que evita que o programador tenha que codificar essas operações manualmente. Um exemplo disso é mostrado abaixo:
operation PrepareSuperposition(qubit : Qubit) : Unit
is Ctl { // Auto-generate the controlled specialization of the operation
H(qubit);
}
Portões de controle clássico
As portas quânticas também podem ser aplicadas após uma medição, onde o resultado da medição atua como um bit de controle clássico.
O símbolo a seguir representa uma porta controlada classicamente, onde $G$ é aplicado condicionado ao bit de controle clássico ser o valor $1$:
Operador de medida
As operações de medição usam um registro de qubit, medem-no e geram o resultado como informações clássicas.
Uma operação de medição é indicada por um símbolo de medidor e sempre usa como entrada um registro de qubit (indicado por uma linha sólida) e gera informações clássicas (indicadas por uma linha dupla). Especificamente, o símbolo da operação de medição se parece com:
Em Q#, o Measure operador implementa a operação de medição.
Exemplo: transformação unitária
Considere a transformação unitária $\text{CNOT}_{01}(H\otimes 1)$. Essa sequência de portas é fundamental para a computação quântica porque cria um estado de dois qubit entrelaçados ao máximo:
$\text{CNOT}_{01}(H\otimes 1)\ket{00}=\frac{1}{\sqrt{2}} (\ket{{00} + \ket{11})$
Operações com essa ou mais complexidade são onipresentes em algoritmos quânticos e correção de erro quântico.
O diagrama de circuito para preparar esse estado quântico entrelaçado máximo é:
O símbolo atrás da porta Hadamard representa uma porta CNOT, onde o círculo preto indica o qubit de controle e a cruz dentro de um círculo indica o target qubit. Esse circuito quântico é representado como se estivesse agindo em dois qubits (ou dois registros equivalentes que consistem em um qubit).
Exemplo: Diagrama de circuito de teletransporte
O teletransporte quântico é um dos melhores algoritmos quânticos para ilustrar componentes de circuitos.
O teletransporte quântico é um protocolo que permite que um estado quântico seja transmitido de um qubit para outro, com a ajuda de um estado emaranhado compartilhado entre o remetente e o receptor e a comunicação clássica entre eles.
Para fins de aprendizado, o remetente é chamado de Alice, o receptor é chamado de Bob e o qubit a ser teletransportado é chamado de qubit de mensagem. Alice e Bob têm um qubit cada, e Alice tem um qubit extra que é o qubit de mensagem.
O diagrama de circuito a seguir ilustra o protocolo de teletransporte:
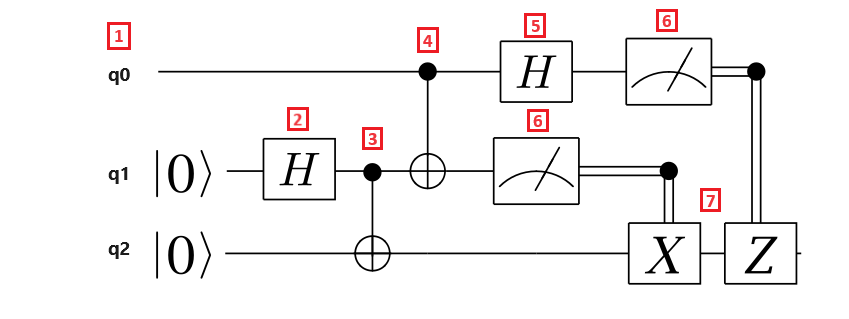
Vamos detalhar as etapas do protocolo de teletransporte:
- O registro de qubit q0 é o qubit de mensagem, o registro de qubit q1 é o qubit de Alice e o registro de qubit q2 é o qubit de Bob. O qubit de mensagem está em um estado desconhecido e os qubits de Alice e Bob estão no $\ket{0}$ estado.
- Uma porta Hadamard é aplicada ao qubit de Alice. Como o qubit está no $\ket{0}$ estado, o estado resultante é $\frac{1}{\sqrt{{2}}(\ket{{0} + ).\ket{1}$
- Uma porta CNOT é aplicada aos qubits de Alice e Bob. O qubit de Alice é o qubit de controle e o qubit de Bob é o target qubit. O estado resultante é $\frac{{1}{\sqrt{2}}(\ket{00} +\ket{{11} ).$ Alice e Bob agora compartilham um estado emaranhado.
- Uma porta CNOT é aplicada ao qubit de mensagem e ao qubit de Alice. Como o qubit de Alice também está emaranhado com o qubit de Bob, o estado resultante é um estado emaranhado de três qubits.
- Um portão Hadamard é aplicado ao qubit de mensagem.
- Alice mede seus dois qubits e informa os resultados da medição para Bob, que não são refletidos no circuito. Os resultados da medição são dois bits clássicos, que podem assumir os valores 00, 01, 10 ou 11.
- Duas portas Pauli controladas classicamente X e Z são aplicadas ao qubit de Bob, dependendo do bit de resultado ser o valor $1$. O estado resultante é o estado do qubit da mensagem original.