Kubit w obliczeniach kwantowych
Podobnie jak bity są podstawowym obiektem informacji w obliczeniach klasycznych, kubity (bity kwantowe) są podstawowym obiektem informacji w obliczeniach kwantowych. Aby zrozumieć tę korespondencję, w tym artykule przedstawiono najprostszy przykład: pojedynczy kubit.
Reprezentowanie kubitu
Bit lub cyfra binarna może mieć wartość 0 lub 1, kubit może mieć wartość $0, $1$ lub kwantową superpozycję $0$$ i $1$.$$$$
Stan pojedynczego kubitu może być opisany przez dwuwymiarowy wektor kolumnowy normy jednostki, czyli wielkość kwadratowa jego wpisów musi być równa $1$. Ten wektor, nazywany wektorem stanu kwantowego, zawiera wszystkie informacje potrzebne do opisania systemu kwantowego z jednym kubitem, tak jak jeden bit zawiera wszystkie informacje potrzebne do opisania stanu zmiennej binarnej. Aby zapoznać się z podstawami wektorów i macierzy w obliczeniach kwantowych, zobacz Vector and matrices (Wektory i macierze).
Każdy dwuwymiarowy wektor kolumnowy liczb rzeczywistych lub złożonych z normą $1$ reprezentuje możliwy stan kwantowy przechowywany przez kubit. W ten sposób $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ reprezentuje stan kubitu, jeśli $\alpha$ i $\beta$ są liczbami zespolonymi spełniającymi $|\alpha|^2 + |\beta|^2 = 1.$
Niektóre przykłady prawidłowych wektorów stanu kwantowego reprezentujących kubity to $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ i $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Te dwa wektory stanowią podstawę dla przestrzeni wektorowej, która opisuje stan kubitu. Oznacza to, że każdy wektor stanu kwantowego może być zapisywany jako suma tych wektorów bazowych. W szczególności wektor x y można zapisać jako $\begin{bmatrix}x \\ 1 \end{bmatrix}$ 0 $ + y \begin{bmatrix} 0 \\ 1 \end{bmatrix}.\begin{bmatrix}\\\end{bmatrix}$ Chociaż każda rotacja tych wektorów będzie służyć jako idealnie prawidłowa podstawa kubitu, jest wybierana ta konkretna, nazywając ją bazą obliczeniową.
Te dwa stany kwantowe są pobierane w celu odpowiadania dwóm stanom klasycznego bitu, a mianowicie $0$ i $1$. Standardowa konwencja jest wybrana
$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}$$$$1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix},$$
chociaż przeciwny wybór może być równie dobrze brany. W związku z tym, z nieskończonej liczby możliwych wektorów stanu kwantowego z jednym kubitem, tylko dwa odpowiadają stanom bitów klasycznych; nie wszystkie inne stany kwantowe.
Mierzenie kubitu
Jak przedstawić objaśnienie kubitu, można uzyskać pewną intuicję dotyczącą tego, co reprezentują te stany, omawiając koncepcję pomiaru. Pomiar odpowiada nieformalnej idei "patrzenia" na kubit, który natychmiast zwija stan kwantowy do jednego z dwóch stanów klasycznych $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ lub $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Gdy kubit podany przez wektor $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ stanu kwantowego jest mierzony, wynik $0$ jest uzyskiwany z prawdopodobieństwem ^2$|\alpha| i wynikiem $1$ z prawdopodobieństwem $$|\beta|^2.$ W wyniku $0$ nowy stan kubitu wynosi $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$; w wyniku $1$ jego stan wynosi $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Należy pamiętać, że te prawdopodobieństwa sumuje się do $1$ ze względu na warunek $|\alpha|normalizacji ^2 + |\beta|^2 1.=$
Właściwości miary oznaczają również, że ogólny znak wektora stanu kwantowego jest nieistotny. Negowanie wektora jest równoznaczne ze $\alpha\rightstrzałką -\alpha$ i $\beta\rightstrzałką -\beta$ . Ponieważ prawdopodobieństwo pomiaru $0$ i $1$ zależy od wielkości kwadratu warunków, wstawianie takich znaków nie zmienia prawdopodobieństwa w ogóle. Takie fazy są często nazywane cudzysłów$$
Ostateczną ważną właściwością pomiaru jest to, że nie musi uszkodzić wszystkich wektorów stanu kwantowego. Jeśli zaczyna się od kubitu w stanie $\begin{bmatrix} 1 \\ 0 , który odpowiada klasycznemu stanowi \end{bmatrix}$0$$, pomiar tego stanu zawsze zwróci wynik $0$ i pozostaw stan kwantowy bez zmian. W tym sensie, jeśli istnieją tylko klasyczne bity (na przykład kubity, które są $\begin{bmatrix}1 \\ 0 \end{bmatrix}$ lub $\begin{bmatrix}0 \\ 1 \end{bmatrix}$), pomiar nie uszkodzi systemu. Oznacza to, że można replikować klasyczne dane i manipulować nimi na komputerze kwantowym tak samo jak na komputerze klasycznym. Jednak możliwość przechowywania informacji w obu stanach jednocześnie jest tym, co podnosi obliczenia kwantowe poza to, co jest możliwe klasycznie i dalsze okrada komputery kwantowe z możliwością kopiowania danych kwantowych masowo, zobacz również twierdzenie bez klonowania.
Wizualizowanie kubitów i przekształceń przy użyciu sfery Bloch
Kubity mogą być również na zdjęciu w 3$D przy użyciu reprezentacji sfery Bloch$. Sfera Bloch umożliwia opisanie stanu kwantowego z jednym kubitem (który jest dwuwymiarowym wektorem złożonym) jako trójwymiarowego wektora wartości rzeczywistej. Jest to ważne, ponieważ pozwala nam wizualizować stany pojedynczego kubitu, a tym samym rozwijać rozumowanie, które mogą być nieocenione w zrozumieniu stanów wielokubitowych (gdzie niestety reprezentacja sfery Bloch rozpada się). Sferę Bloch można wizualizować w następujący sposób:
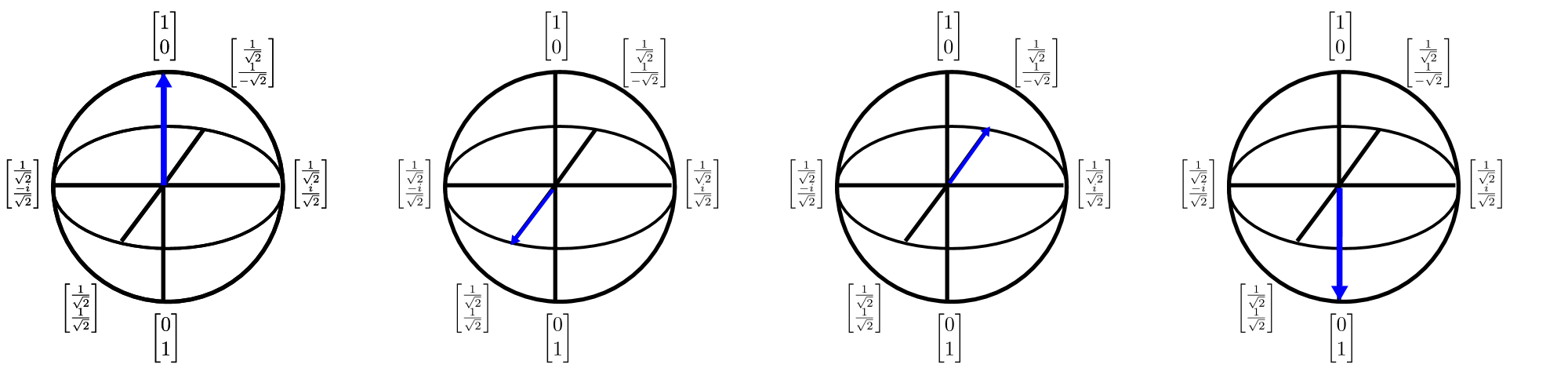
Strzałki na tym diagramie pokazują kierunek, w którym wektor stanu kwantowego wskazuje, a każda transformacja strzałki może być uważana za obrót o jednej z osi kardynaalnych. Podczas myślenia o obliczeniach kwantowych jako sekwencji rotacji jest potężna intuicja, trudno jest użyć tej intuicji do projektowania i opisywania algorytmów. Q# Zapobiega temu problemowi, podając język opisujący takie rotacje.
Operacje pojedynczego kubitu
Komputery kwantowe przetwarzają dane, stosując uniwersalny zestaw bram kwantowych, które mogą emulować dowolną rotację wektora stanu kwantowego. To pojęcie uniwersalności jest związane z pojęciem uniwersalności dla tradycyjnych (na przykład klasycznych) obliczeń, w których zestaw bram jest uważany za uniwersalny, jeśli każda transformacja bitów wejściowych może być wykonywana przy użyciu obwodu o długości skończonej. W obliczeniach kwantowych prawidłowe przekształcenia, które możemy wykonać na kubitie, to przekształcenia jednostkowe i pomiary. Operacja przylegania lub złożona transponacja konjugatu ma kluczowe znaczenie dla obliczeń kwantowych, ponieważ jest ona potrzebna do odwrócenia przekształceń kwantowych.
Operacje jednokubitowe lub bramy kwantowe z jednym kubitem można podzielić na dwie kategorie: bramy Clifforda i bramy spoza Cliffordu. Bramy non-Clifford składają się tylko z $bramy T$ (znanej również jako brama $\pi/8$ ).
$$ T=\begin{bmatrix} 1 & 0 \ 0 & e^{i\pi/4}\end{bmatrix}. $$
Standardowy zestaw bram Cliffordów z jednym kubitem, dołączony domyślnie w systemie Q#, obejmują
$$ H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \ 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 \ 0 & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 \ 1& 0 \end{bmatrix}= HT^4H, $$
$$ Y =\begin{bmatrix} 0 & -i \ i & 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1& 0\ 0&-1 \end{bmatrix}=T^4. $$
Tutaj operacje $X$, $Y$ i $Z$ są używane szczególnie często i są nazywane operatorami Pauli po ich twórca Wolfgang Pauli. Wraz z bramą inną niż Clifford (brama $T$) operacje te mogą być komponowane, aby przybliżyć dowolną transformację jednostkową na jednym kubitie.
Chociaż poprzednie stanowią najbardziej popularne bramy pierwotne do opisywania operacji na poziomie logicznym stosu (należy traktować poziom logiczny jako poziom algorytmu kwantowego), często wygodne jest rozważenie mniej podstawowych operacji na poziomie algorytmu, na przykład operacji bliżej poziomu opisu funkcji. Q# Na szczęście dostępne są również metody implementowania jednostek wyższego poziomu, które z kolei umożliwiają implementowanie algorytmów wysokiego poziomu bez jawnego rozkładania wszystkich elementów w dół do bram Clifford i $T$.
Najprostszym takim pierwotnym jest pojedynczy kubit-rotacja. Trzy rotacje pojedynczego kubitu są zwykle brane pod uwagę: $R_x$, $R_y$ i $R_z$. Aby zwizualizować akcję obrotu $R_x(\theta)$, załóżmy na przykład, że wskazujesz prawy kciuk wzdłuż kierunku $osi x$ sfery Bloch i obracając wektor ręką za pomocą kąta $radianów \theta/2$ . Ten mylący czynnik $2$ wynika z faktu, że wektory ortogone są $180^\circ$ od siebie po wykreśleniu na sferę Blocha, ale rzeczywiście $są 90^\circ$ stopnie od siebie geometrycznie. Odpowiednie macierze jednostkowe to:
$$ \begin{align*}& R_z(\theta) = e^{-i\theta Z/2}=\begin{bmatrix} e^{-i\theta/2}& 0\\ 0& e^{i\theta/2}\end{bmatrix}, \\& R_x(\theta) = e^{-i\theta X/2}= HR_z(\theta)H =\begin{bmatrix} \cos(\theta/2) & -i\sin(\theta/2)\\ -i\sin(\theta/2) & \cos(\theta/2) \end{bmatrix}, \\& R_y(\theta) = e^{-i\theta Y/2}= SHR_z(\theta)HS^\dagger=\begin{bmatrix} \cos(\theta/2) & -\sin(\theta/2)\\ \sin(\theta/2) & \cos(\theta/2) \end{bmatrix}. \end{wyrównać*}$$
Podobnie jak wszystkie trzy obrotu można połączyć ze sobą, aby wykonać dowolną rotację w trzech wymiarach, można go również zobaczyć z reprezentacji sfery Bloch, że każda macierz jednostkowa może być napisana jako sekwencja trzech rotacji. W szczególności dla każdej macierzy $jednostkowej U$ istnieje $\alpha\beta\gamma\delta$, tak że $U=^{i\alpha} R_x(\beta)R_z(\gamma)R_x(\delta).$ W związku z tym $R_z(\theta)$ i $H$ również tworzą uniwersalny zestaw bramek, chociaż nie jest to zestaw dyskretny, ponieważ $\theta$ może przyjmować dowolną wartość. Z tego powodu i ze względu na aplikacje w symulacji kwantowej takie bramy ciągłe mają kluczowe znaczenie dla obliczeń kwantowych, zwłaszcza na poziomie projektowania algorytmu kwantowego. Aby osiągnąć implementację sprzętu odpornego na uszkodzenia, zostaną one ostatecznie skompilowane w sekwencje dyskretnych bram, które ściśle przybliżają te rotacje.