Konwencje diagramu obwodu kwantowego

Czasami algorytmy kwantowe są łatwiejsze do zrozumienia na diagramie obwodu niż w równoważnej reprezentacji macierzy pisanej. W tym artykule wyjaśniono, jak odczytywać diagramy obwodów kwantowych i ich konwencje.

Aby uzyskać więcej informacji, zobacz Jak wizualizować diagramy obwodów kwantowych.

Odczytywanie diagramów obwodów kwantowych

W obwodzie kwantowym czas przepływa od lewej do prawej. Bramy kwantowe są uporządkowane w kolejności chronologicznej z najbardziej lewą bramą, ponieważ brama po raz pierwszy zastosowana do kubitów.

Skorzystaj z następującego diagramu obwodu kwantowego jako przykładu:

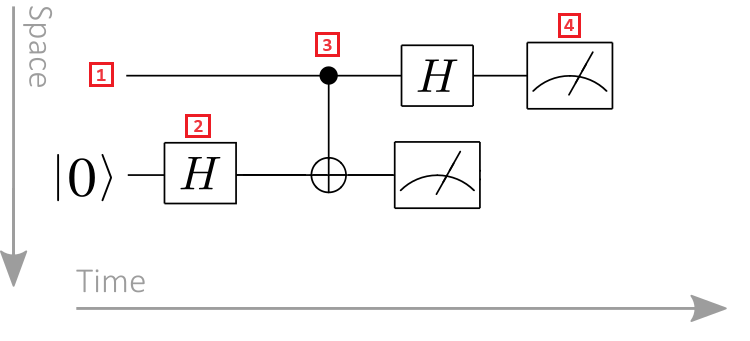
1. Rejestr kubitów: rejestry kubitów są wyświetlane jako linie poziome, a każda linia reprezentuje kubit. Górna linia to rejestr kubitów oznaczony jako 0, drugi wiersz to rejestr kubitów oznaczony etykietą 1 itd.
2. Bramka kwantowa: Operacje kwantowe są reprezentowane przez bramy kwantowe. Termin bramka kwantowa jest analogiczna do klasycznych bram logiki. Bramy działające na co najmniej jednym rejestrze kubitów są oznaczone jako pole. W tym przykładzie symbol reprezentuje operację Hadamard.
3. Kontrolowana bramka: Kontrolowane bramy działają na co najmniej dwóch kubitach. W tym przykładzie symbol reprezentuje bramę CNOT. okrąg reprezentuje kubit kontrolny, a krzyż w okręgu target reprezentuje kubit.
4. Operacja pomiaru: symbol miernika reprezentuje operację pomiaru. Operacja pomiaru przyjmuje rejestr kubitów jako dane wejściowe i wyjściowe informacji klasycznych.

Stosowanie bram kwantowych

Ponieważ czas przepływa od lewej do prawej, brama z lewej strony jest stosowana jako pierwsza, na przykład akcja następującego obwodu kwantowego jest jednostkową macierzą $CBA$.

Uwaga

Mnożenie macierzy jest zgodne z przeciwną konwencją: najpierw stosuje się macierz z prawej strony. Jednak na diagramach obwodów kwantowych najpierw zastosowano lewą bramę. Ta różnica może czasami prowadzić do nieporozumień, dlatego ważne jest, aby zauważyć tę znaczącą różnicę między notacją liniową a diagramami obwodów kwantowych.

Dane wejściowe i wyjściowe obwodów kwantowych

Na diagramie obwodu kwantowego przewody wchodzące do bramy kwantowej reprezentują kubity wejściowe do bramy kwantowej, a przewody wychodzące z bramy kwantowej reprezentują kubity wyjściowe z bramy kwantowej.

Liczba danych wejściowych bramy kwantowej jest równa liczbie danych wyjściowych bramy kwantowej. Dzieje się tak dlatego, że operacje kwantowe są jednoczesne i dlatego odwracalne. Gdyby brama kwantowa miała więcej danych wyjściowych niż dane wejściowe, nie byłaby odwracalna, a tym samym nie unitary, co jest sprzecznością.

Z tego powodu każde pole narysowane na diagramie obwodowym musi mieć dokładnie taką samą liczbę przewodów, które wchodzą do niego jako wyjście.

Operacje z wieloma kubitami

Diagramy obwodów z wieloma kubitami są zgodne z podobnymi konwencjami do jednego kubitu. Na przykład można zdefiniować $operację $jednostkową B$ z dwoma kubitami ( H S\otimes X),$ więc równoważny obwód kwantowy jest następujący:

B można również wyświetlić $$ jako akcję w jednym rejestrze dwóch kubitów, a nie dwóch rejestrach z jednym kubitem w zależności od kontekstu, w którym jest używany obwód.

Być może najbardziej przydatną właściwością takich diagramów obwodów abstrakcyjnych jest to, że umożliwiają one opisywanie skomplikowanych algorytmów kwantowych na wysokim poziomie bez konieczności kompilowania ich do podstawowych bram. Oznacza to, że można uzyskać intuicję dotyczącą przepływu danych dla dużego algorytmu kwantowego bez konieczności zrozumienia wszystkich szczegółów działania każdej z podrouty w algorytmie.

Kontrolowane bramy

Bramy sterowane kwantowo to bramy dwukabitowe, które stosują bramę z jednym kubitem do kubitu target , jeśli kubit kontrolny jest w określonym stanie.

Rozważmy na przykład bramę kontrolowaną kwantowo, oznaczona $\Lambda(G)$, gdzie wartość pojedynczego $kubitu kontroluje zastosowanie operacji G$ . Kontrolowana brama $\Lambda(G)$ można zrozumieć, patrząc na poniższy przykład danych wejściowych stanu produktu:

$\Lambda(G) (\alpha\ket{{0} + \beta\ket{1}) \ket{\psi}\alpha\ket{\psi}\ket{{0}=+ G \beta\ket{{1}\ket{\psi}$

Oznacza to, że kontrolowana brama stosuje $G$ do rejestru zawierającego $\psi$ , jeśli i tylko wtedy, gdy kubit kontrolny przyjmuje wartość $1$. Ogólnie rzecz biorąc, takie kontrolowane operacje są opisane na diagramach obwodów za pomocą następującego symbolu:

W tym miejscu okrąg oznacza bit kwantowy, na którym brama jest kontrolowana, a pionowy drut oznacza unitary, który jest stosowany, gdy kubit kontrolny przyjmuje wartość $1$.

W przypadku przypadków specjalnych, w których $G=X$ i $G=Z$, następująca notacja jest używana do opisywania kontrolowanej wersji bram (należy pamiętać, że brama kontrolowana X jest bramą CNOT):

Q# Udostępnia metody automatycznego generowania kontrolowanej wersji operacji, co pozwala programistom na przekazanie kodu tych operacji. Poniżej przedstawiono przykład:

operation PrepareSuperposition(qubit : Qubit) : Unit
is Ctl { // Auto-generate the controlled specialization of the operation
    H(qubit);
}

Bramy sterowane klasycznie

Bramy kwantowe można również stosować po pomiarze, gdzie wynik pomiaru działa jako klasyczny bit kontrolny.

Poniższy symbol reprezentuje klasycznie kontrolowaną bramę, gdzie $G$ jest stosowana warunkowo dla klasycznego bitu sterującego o wartości 1:$$

Operator pomiaru

Operacje pomiaru przyjmują rejestr kubitów, mierzy go i generuje wynik jako informacje klasyczne.

Operacja pomiaru jest oznaczona symbolem miernika i zawsze przyjmuje jako dane wejściowe rejestr kubitów (oznaczony linią ciągłą) i zwraca informacje klasyczne (oznaczone podwójnym wierszem). W szczególności symbol operacji pomiaru wygląda następująco:

W Q#systemie Measure operator implementuje operację pomiaru.

Przykład: Przekształcanie jednostkowe

Rozważ przekształcenie $\text{ jednostkowe CNOT}_({01}H\otimes 1)$. Ta sekwencja bramy ma podstawowe znaczenie dla obliczeń kwantowych, ponieważ tworzy maksymalnie splątany stan dwóch kubitów:

$\mathrm{CNOT}_({01}H\otimes 1)\ket{00}\left=\frac{1}{\sqrt{2}}({00}\ket{ + ), \ket{11}\right$

Operacje z tą lub większą złożonością są wszechobecne w algorytmach kwantowych i korekcie błędów kwantowych.

Diagram obwodu do przygotowania tego maksymalnie splątanego stanu kwantowego to:

Symbol za bramą Hadamard reprezentuje bramę CNOT, gdzie okrąg wskazuje kubit kontrolny, a krzyż w okręgu target wskazuje kubit. Ten obwód kwantowy jest przedstawiany jako działający na dwóch kubitach (lub równoważne dwa rejestry składające się z jednego kubitu).

Przykład: diagram obwodu teleportacji

Teleportacja kwantowa jest jednym z najlepszych algorytmów kwantowych ilustrujących składniki obwodu.

Teleportacja kwantowa to protokół, który umożliwia przesyłanie stanu kwantowego z jednego kubitu do innego przy użyciu współużytkowanego stanu splątanego między nadawcą a odbiornikiem i klasyczną komunikacją między nimi.

W celach szkoleniowych nadawca nosi nazwę Alice, odbiornik jest nazywany Bobem, a kubit do teleportowania jest nazywany kubitem komunikatu. Alicja i Bob posiadają jeden kubit, a Alicja ma dodatkowy kubit, który jest kubitem komunikatu.

Na poniższym diagramie obwodu przedstawiono protokół teleportacji:

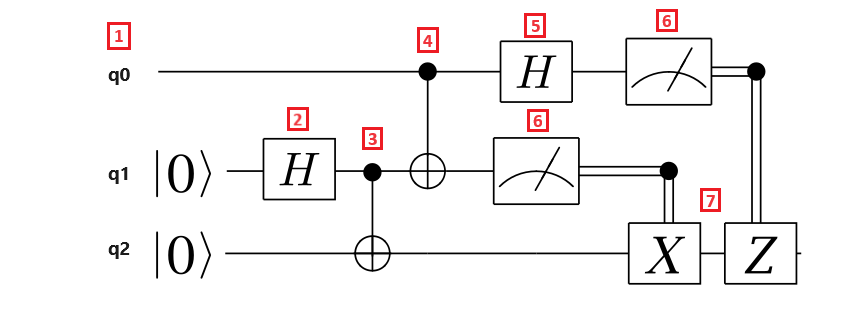
Przeanalizujmy kroki protokołu teleportacji:

1. Rejestr kubitów q0 to kubit komunikatu, rejestr kubitów q1 to kubit Alicji, a rejestr kubitów q2 to kubit Boba. Kubit komunikatu jest w nieznanym stanie, a kubity Alice i Boba są w $\ket{0}$ stanie.
2. Brama Hadamard jest stosowana do kubitu Alicji. Ponieważ kubit jest w $\ket{0}$ stanie, wynikowy stan to $\frac{1}{\sqrt{{2}}(\ket{{0} + \ket{1})$.
3. Brama CNOT jest stosowana do kubitów Alice i Boba. Kubit Alicji jest kubitem sterującym, a kubit Boba jest kubitem target . Wynikowy stan to $\frac{{1}{\sqrt{2}}(\ket{00} + \ket{{11})$. Alicja i Bob mają teraz splątane stany.
4. Brama CNOT jest stosowana do kubitu komunikatu i kubitu Alicji. Ponieważ kubit Alicji jest również splątany kubitem Boba, wynikowy stan jest stanem splątania trzech kubitów.
5. Brama usługi Hadamard jest stosowana do kubitu komunikatu.
6. Alicja mierzy dwa kubity i informuje wyniki pomiaru do Boba, który nie jest odzwierciedlony w obwodzie. Wyniki pomiaru to dwa klasyczne bity, które mogą przyjmować wartości 00, 01, 10 lub 11.
7. Dwa klasycznie kontrolowane bramy Pauli X i Z są stosowane do kubitu Boba, w zależności od bitu wyniku wynosi $1$. Stan wynikowy to oryginalny stan kubitu komunikatu.

Powiązana zawartość

• Splątanie kwantowe
• Algorytm Grovera
• Reprezentacja kwantowa pośrednia
• Wektory i macierze