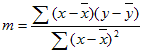WorksheetFunction.LinEst 方法 (Excel)

通过使用最小二乘法计算出最适合数据的直线来计算直线的统计信息，并返回描述该直线的数组。 因为此函数返回数值数组，所以必须以数组公式的形式输入。

语法

表达式。LinEst (Arg1、 Arg2、 Arg3、 Arg4)

表达 一个代表 WorksheetFunction 对象的变量。

参数

名称	必需/可选	数据类型	说明
Arg1	必需	Variant	Known_y - 在关系 y = mx + b 中已知道的 y 值集。
Arg2	可选	Variant	Known_x's - 关系表达式 y = mx + b 中可能已知的可选 x 值集合。
Arg3	可选	Variant	Const - 一个逻辑值，用于指定是否强制常量 b 等于 0。
Arg4	可选	Variant	Stats - 一个逻辑值，指定是否返回附加回归统计值。

返回值

Variant

说明

如果存在多个 x 值范围) ，则行的公式为 y = mx + b 或 y = m1x1 + m2x2 + ... + b (，其中从属 y 值是独立 x 值的函数。 M 值是与每个 x 值相对应的系数，b 为常量。 注意 y、x 和 m 可以是向量。 LinEst 返回的数组是 {mn,mn-1,...,m1,b}。 LinEst 还可以返回其他回归统计信息。

如果数组known_y位于单个列中，则 known_x 的每一列都解释为一个单独的变量。

如果数组known_y位于单个行中，则 known_x 的每一行都解释为一个单独的变量。

数组 known_x's 可以包含一组或多组变量。 如果只用到一个变量，只要 known_y's 和 known_x's 维数相同，它们就可以是任何形状的区域。 如果用到多个变量，则 known_y's 必须为向量（即必须为一行或一列）。

如果省略known_x，则假定它是大小与 known_y 相同的数组 {1,2,3,...} 。

• 如果 const 为 True 或省略，则正常计算 b。

• 如果 const 为 False，则 b 设置为 0，并将 m 值调整为适合 y = mx。

• 如果统计信息为 True， 则 LinEst 返回其他回归统计信息，因此返回的数组为 {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid}。

• 如果统计信息为 False 或省略， LinEst 仅返回 m 系数和常量 b。

附加回归统计值如下：

回归统计信息	Description
se1，se2,...,sen	系数 m1,m2,...,mn 的标准误差值。
Seb	当 const 为 False) 时，常量 b (seb = #N/A 的标准错误值。
R 2	判定系数。 Y 的估计值与实际值之比，范围在 0 到 1 之间。 如果为 1，则样本中有一个完全相关 -- 估计的 y 值与实际 y 值之间没有差异。 如果判定系数为 0，则回归公式不能用来预测 Y 值。
sey	y 估计值的标准误差。
F	F 统计或 F 观察值。 使用 F 统计可以判断因变量和自变量之间是否偶尔发生过可观察到的关系。
Df	自由度。 用于在统计表上查找 F 临界值。 将表中的值与 LinEst 返回的 F 统计信息进行比较，以确定模型的置信度级别。
ssreg	回归平方和。
ssresid	残差平方和。

下面的图示显示了附加回归统计值返回的顺序。

可以使用斜率和 y 截距来描述任何直线： Slope (m)。 若要查找通常写为 m 的直线的斜率，请在直线上取两个点， (x1，y1) ， (x2，y2) ：斜率等于 (y2 - y1) / (x2 - x1) 。 Y 截距 (b) ：线条的 y 截距（通常写为 b）是该直线与 y 轴交界处的 y 值。 直线的公式为 y = mx + b。 知道 m 和 b 的值后，可以通过将 y 值或 x 值插入该公式来计算线条上的任意点。 还可以使用 TREND 函数。

如果只有一个独立的 x 变量，则可以使用以下公式直接获取斜率和 y 截距值：

• 边坡： =INDEX(LINEST(known_y's,known_x's),1)
• Y 截距： =INDEX(LINEST(known_y's,known_x's),2)

LinEst 计算的线条的准确性取决于数据中的散点程度。 数据越是线性， LinEst 模型就越准确。 LinEst 使用最小二乘法来确定数据的最佳拟合度。 如果只有一个独立的 x 变量，则 m 和 b 的计算基于以下公式：

其中 x 和 y 是样本平均值，即 x = AVERAGE (已知 x 的) ，y = AVERAGE (known_y 的) 。

直线和曲线拟合函数 LinEst 和 LogEst 可以计算适合数据的最佳直线或指数曲线。 但是，必须确定两个结果中哪一个最适合你的数据。 可以计算 TREND(known_y's,known_x's) 直线或 GROWTH(known_y's, known_x's) 指数曲线。 这些函数在没有new_x参数的情况下，返回沿实际数据点沿该直线或曲线预测的 y 值的数组。 然后，可以将预测值与实际值进行比较。 你可能想要为两者绘制图表，以便进行视觉比较。

在 回归分析中，Microsoft Excel 为每个点计算该点估计的 y 值与其实际 y 值之间的平方差。 这些平方差之和称为残差平方和 (ssresid)。 然后，Excel 计算正方形的总和（sstotal）。 当 const = TRUE 或被删除时，总平方和是 y 的实际值和平均值的平方差之和。 当 const = FALSE 时，总平方和是 y 的实际值的平方和（不需要从每个 y 值中减去平均值）。 然后，可以在 中找到 ssreg = sstotal - ssresid平方的回归总和，即 ssreg。 与平方的总和相比，剩余平方和越小，确定系数 r2 的值就越大，这是回归分析得出的公式解释变量之间关系的指标：r2 等于 ssreg/sstotal。

在某些情况下，一个或多个 X 列 (假定 Y 和 X 列位于列中，) 在其他 X 列存在的情况下可能没有其他预测值。 换句话说，删除一个或多个 X 列可能并不影响 Y 预测值的精度。 在这种情况下，应在回归模型中省略这些冗余的 X 列。 这种现象称为 共线， 因为任何冗余 X 列都可以表示为非冗余 X 列的倍数之和。 LinEst 检查共线，并在识别出 X 列时从回归模型中删除任何冗余的 X 列。 删除的 X 列可在 LinEst 输出中识别为系数为 0 和 0 se。

• 如果删除一个或多个冗余列，则 df 会受到影响，因为 df 依赖于实际用于预测目的的 X 列数。 如果由于删除冗余的 X 列而改变了 df，则 sey 和 F 的值也会受到影响。
• 实际上，共线性应该相对稀有。 但是，当某些 X 列仅包含 0 和 1 作为实验中的主体是否是特定组的成员的指示符时，这种情况更有可能出现。 如果 const = TRUE 或省略， LinEst 会有效地插入所有 1 的附加 X 列来为截距建模。 如果你有一个列，每个主题为 1，如果不是，则为 0，如果不是，则每个主题也有一个为 1 的列，如果不是，则为 0，则后一列是多余的，因为可以从 LinEst 添加的所有 1 的附加列中的条目中减去男性指示器列中的条目来获取。
• 当由于共线性而没有从模型中删除 X 列时，df 的计算方式如下：如果有 k 列的 known_x 和 const = TRUE 或省略，则 df = n - k - 1为 。 如果 const = FALSE，则为 df = n - k。 在这两种情况下，只要因共线性删除一个 X 列，df 就会加 1。

对于返回结果为数组的公式，必须以数组公式的形式输入。

• 当输入一个数组常量（如 known_x's）作为参数时，用逗号来分隔同一行中的值，用分号来分隔不同的行。 分隔符可能因“控制面板”中的“区域和语言选项”中区域设置的不同而有所不同。
• 注意，如果 y 的回归分析预测值超出了用来计算公式的 y 值的范围，它们可能是无效的。

LinEst 函数中使用的基础算法不同于 Slope 和 Intercept 函数中使用的基础算法。 这些算法间的差异可能在共线数据不确定时导致不同的结果。 例如，如果 known_y's 参数的数据点个数为 0，而 known_x's 参数的数据点个数为 1：

• LinEst 返回值 0。 LinEst 算法旨在返回共线数据的合理结果，在这种情况下，至少可以找到一个答案。
• 斜率 和 截距 返回#DIV/0！ 错误。 斜率和截距算法旨在查找一个且仅一个答案，在这种情况下，可以有多个答案。

支持和反馈

有关于 Office VBA 或本文档的疑问或反馈？ 请参阅 Office VBA 支持和反馈，获取有关如何接收支持和提供反馈的指南。