Проверка гипотезы с помощью t-Test
Важно!
Поддержка Студии машинного обучения (классической) будет прекращена 31 августа 2024 г. До этой даты рекомендуется перейти на Машинное обучение Azure.
Начиная с 1 декабря 2021 года вы не сможете создавать новые ресурсы Студии машинного обучения (классической). Существующие ресурсы Студии машинного обучения (классическая версия) можно будет использовать до 31 августа 2024 г.
- См. сведения о перемещении проектов машинного обучения из ML Studio (классической) в Машинное обучение Azure.
- См. дополнительные сведения о Машинном обучении Azure.
Поддержка документации по ML Studio (классической) прекращается, а сама документация может не обновляться в будущем.
Сравнивает значения из двух столбцов с помощью t-теста
Категория: статистические функции
Примечание
Область применения: только Машинное обучение Studio (классическая версия)
Подобные модули перетаскивания доступны в конструкторе машинного обучения Azure.
Обзор модуля
В этой статье описывается использование тестовой гипотезы с помощью модуля t-Test в Машинное обучение Studio (классическая модель) для создания оценок для трех типов t-тестов:
- Одновыборочный t-тест
- Парный t-тест
- Непарный t-тест
Обычно T-тест помогает определить, отличаются ли средние значения двух определенных групп. Предположим, например, что вам нужно оценить проверочные данные для пациентов, которые принимали лекарство A, и для пациентов, которые принимали лекарство B, а также сравнить метрику скорости выздоровления в обеих группах. Согласно нулевой гипотезе скорость выздоровления одинакова в обеих группах, а значения скорости выздоровления в них имеют нормальное распределение.
С помощью тестовой гипотезы с помощью t-test и предоставления столбцов, содержащих коэффициенты восстановления в качестве входных данных, можно получить оценки, указывающие, является ли разница значимой, что означает, что пустая гипотеза должна быть отклонена. В тесте учитываются такие факторы, как разница между значениями, размер выборки (чем больше, тем лучше) и стандартное отклонение (чем меньше, тем лучше).
Просмотрив результаты тестовой гипотезы с помощью модуля t-Test , вы можете определить, является ли пустая гипотеза истинной или ЛОЖНОй, и проверить оценки достоверности (P) из t-теста.
Выбор t-теста
Выберите один пример t-теста при применении следующих условий:
Имеется одна выборка показателей.
Все показатели не зависят друг от друга.
Выборочное распределение xˉ является нормальным.
Как правило, T-тест с одной выборкой используется для сравнения среднего значения и известного количества.
Выберите парный t-тест при применении следующих условий:
Имеется совпадение пар оценок. Например, это могут быть два разных показателя одного человека или совпадение показателей двух человек (например, мужа и жены).
Каждая пара показателей независима от любой другой пары.
Распределение выборки d является нормальным.
Парный Т-тест подходит для сравнения связанных случаев. Средняя разница между оценками парных случаев позволяет определить, насколько статистически значима общая разница.
Выберите непарный t-тест при применении следующих условий:
Имеется две независимых выборки показателей. То есть нет оснований для установления парности оценок в выборке 1 и в выборке 2.
Любые показатели в выборке не зависят от всех остальных показателей в той же выборке.
Распределение выборки x1–x2 является нормальным.
Кроме того, может соблюдаться дополнительное требование приблизительного совпадения дисперсии в группах.
Настройка тестовой гипотезы с помощью t-test
Используйте один набор данных в качестве входных данных. Сравниваемые столбцы должны находиться в одном наборе данных.
Если необходимо сравнить столбцы из разных наборов данных, можно изолировать каждый столбец для сравнения с помощью команды Select Columns в наборе данных, а затем объединить их в один набор данных с помощью команды "Добавить столбцы".
Добавьте тестовую гипотезу с помощью модуля t-Test в эксперимент.
Этот модуль можно найти в категории статистических функций в Студии (классической).
Добавьте набор данных, содержащий столбец или столбцы, которые требуется проанализировать.
Определите, какой тип t-теста подходит для ваших данных. Узнайте , как выбрать t-test.
Один пример: если вы используете один пример, задайте следующие параметры:
Нулевая гипотеза μ: введите значение, которое будет использоваться в качестве значения, предполагающего значение NULL для примера. Это указывает ожидаемое среднее значение, по которому будет проверено среднее значение выборки.
Целевой столбец: используйте селектор столбцов, чтобы выбрать один числовый столбец для тестирования.
Тип гипотезы: выберите тест с одним или двумя хвостами. Значение по умолчанию — двусторонний тест. Это наиболее распространенный тип теста, в котором ожидаемое распределение симметрично относительно нуля.
Параметр One Tail GT предназначен для одного хвоста больше, чем тест. Этот тест дает больше возможностей для обнаружения эффекта в одном направлении, не проверяя эффект в другом направлении.
Параметр One Tail LT дает одностороннее , чем тест.
α. Укажите коэффициент достоверности. Это значение используется для оценки значения P (первого вывода модуля). Если значение p меньше коэффициента достоверности, то отклонена пустая гипотеза.
PairedSamples: при сравнении двух выборок из одной совокупности задайте следующие параметры:
Нулевая гипотеза μ: введите значение, представляющее разницу выборки между парой образцов.
Целевой столбец: используйте селектор столбцов, чтобы выбрать два числовых столбца для тестирования.
Тип гипотезы: выберите одностороннюю или двухстороннюю проверку. Значение по умолчанию — двусторонний тест.
α. Укажите коэффициент достоверности. Это значение используется для оценки значения P (первый вывод модуля)> Если p меньше коэффициента достоверности, то отклонена пустая гипотеза.
НепараныеSamples: при сравнении двух неспарных выборок задайте следующие параметры:
- Предположим, что одинаковое отклонение: отмените выборку, если выборки из разных групп населения.
- Нулевая гипотеза μ1: введите среднее значение для первого столбца.
- Нулевая гипотеза μ2: введите среднее значение для второго столбца.
- Целевые столбцы: используйте селектор столбцов, чтобы выбрать два числовых столбца для тестирования.
- Тип гипотезы: указывает, является ли тест одним или двумя хвостами. Значение по умолчанию — двусторонний тест.
- α. Укажите коэффициент достоверности. Это значение используется для оценки значения P (первый вывод модуля)> Если p меньше коэффициента достоверности, то отклонена пустая гипотеза.
Запустите эксперимент.
Результаты
Выходные данные модуля — это набор данных, содержащий оценки t-тестов, и преобразование, которое можно дополнительно сохранить для повторного применения к этому или другому набору данных с помощью метода Apply Transformation.
Набор данных оценок содержит эти значения независимо от типа используемого t-теста:
- Оценка вероятности, указывающая на достоверность нулевой гипотезы
- Значение, указывающее, должна ли быть отклонена нулевая гипотеза.
Совет
Помните, что цель — определить, можно ли отклонить пустую гипотезу. Оценка 0 не означает, что вы должны принять пустую гипотезу: это означает, что у вас недостаточно данных и требуется дальнейшее исследование.
Технические примечания
Модуль автоматически именует выходные столбцы в соответствии со следующими соглашениями в зависимости от выбранного типа t-теста и от отклонения или принятия нулевой гипотезы.
При использовании входных столбцов с именами {0} и {1}модуль создает следующие имена:
| Столбцы | SingleSampleSet | PairedSamples | UnpairedSamples |
|---|---|---|---|
| Выходной столбец P | P_ss({0}) | P_ps({0}, {1}) | P_us({0}, {1}) |
| Выходной столбец RejectH0 | RejectH0_ss({0})" | RejectH0_ps({0}, {1}) | RejectH0_us({0}, {1}) |
Как вычисляются оценки
Этот модуль вычисляет и использует стандартное отклонение выборки; таким образом, уравнение используется (n-1) в знаменателе.
Оценки вычислений для одно примерного теста
При условии одной выборки оценок, не зависящих друг от друга, и нормального распределения, оценка вычисляется следующим образом.
Примите следующие входные данные:
- Один столбец значений из набора данных
- Параметр μ0 нулевой гипотезы (H0)
- Показатель достоверности, заданный значением α
Извлеките количество выборок (n).
Вычислите среднее значение для выборочных данных.
Вычислите стандартное отклонение (s) данных выборки.
Вычисление t и степеней свободы (df):
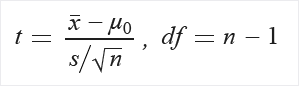
Извлечение вероятности P из таблицы распределения T с помощью t и df.
Оценки вычислений для парного t-теста
С учетом сопоставленного набора оценок, где каждая пара независима от другой, и нормального распределения в каждом наборе, оценка вычисляется следующим образом.
Примите следующие входные данные:
- Два столбца значений из набора данных
- Параметр нулевой гипотезы (H0) d0
- Показатель достоверности, заданный значением α
Извлеките несколько примеров пар (n).
Вычислите среднее значение разностей для выборочных данных.
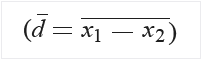
Вычислите стандартное отклонение различий (sd).
Вычисление t и степени свободы (df):
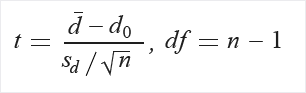
Извлеките вероятность (P) из таблицы распределения (T) с помощью t и df.
Оценки вычислений для непарного t-теста
При условии двух независимых выборок оценок с нормальным распределением значений в каждой выборке оценка вычисляется следующим образом.
Примите следующие входные данные:
- Набор данных, содержащий два столбца
doubles - Параметр нулевой гипотезы (H0) (d0)
- Показатель достоверности, заданный значением α
- Набор данных, содержащий два столбца
Извлеките несколько примеров в каждой группе, n1 и n2.
Вычислите средние значения для каждого набора выборок.
Вычислите стандартное отклонение для каждой группы как s1 и s2.
Вычисление t и степеней свободы (df):
Кроме того, может быть соблюдено дополнительное требование приблизительного совпадения значений дисперсии в группах, как показано ниже.
Сначала вычислите общее среднеквадратичное отклонение:
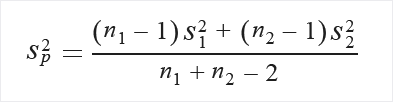
Если не предполагается, что дисперсии равны, используйте для вычисления следующую формулу.
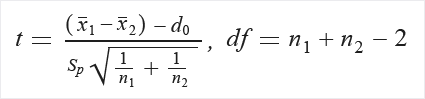
Извлеките P из таблицы распределения (T) с помощью t и df.
Вычисление нулевой гипотезы
Вероятность нулевой гипотезы, обозначенной как P, вычисляется следующим образом:
Если P < α, установите для флага "Отклонить" значение True.
Если P ≥ α, установите для флага "Отклонить" значение False.
Ожидаемые входные данные
| Имя | Тип | Описание |
|---|---|---|
| Dataset | Таблица данных | Входной набор данных |
Параметры модуля
| Имя | Диапазон | Тип | По умолчанию | Описание |
|---|---|---|---|---|
| Тип гипотезы | Любой | Гипотеза | Двусторонний | Тип нулевой гипотезы t-теста Стьюдента |
| Значение μ для нулевой гипотезы | Любой | Float | 0,0 | Для одновыборочного t-теста — выборочное среднее при нулевой гипотезе. Для парного t-теста — выборочная разность. |
| Целевые столбцы | Любой | Выбор столбцов | Нет | Шаблон выбора целевых столбцов |
| Предположение равных дисперсий | Любой | Логическое значение | True | Предполагается, что дисперсии двух выборок равны. Применяется только к непарным выборкам. |
| μ1 для нулевой гипотезы | Любой | Float | 0,0 | Среднее арифметическое значение первой выборки для нулевой гипотезы |
| α | [0.0;1.0] | Float | 0,95 | Показатель достоверности (если P меньше показателя достоверности, нулевая гипотеза отклоняется) |
Выходные данные
| Имя | Тип | Описание |
|---|---|---|
| P | Таблица данных | Оценка вероятности, указывающая на достоверность нулевой гипотезы |
| Reject H0 | Таблица данных | Значение, указывающее, должна ли быть отклонена нулевая гипотеза |
Исключения
| Исключение | Описание |
|---|---|
| Ошибка 0003 | Исключение возникает, если один или несколько входных аргументов имеют значение NULL или пусты. |
| Ошибка 0008 | Исключение возникает, если параметр находится за пределами диапазона. |
| Ошибка 0017 | Исключение возникает, если один или несколько указанных столбцов относятся к типу, который не поддерживается в текущем модуле. |
| Ошибка 0020 | Исключение возникает, если количество столбцов в некоторых наборах данных, переданных модулю, слишком мало. |
| Ошибка 0021 | Исключение возникает, если количество строк в некоторых наборах данных, переданных модулю, слишком мало. |
| Ошибка 0031 | Исключение возникает, если количество столбцов в наборе столбцов меньше, чем требуется. |
| Ошибка 0032 | Исключение возникает, если аргумент не является числом. |
| Ошибка 0033 | Исключение возникает, если аргумент — бесконечность. |
Список ошибок, относящихся к модулям Студии (классическая модель), см. в Машинное обучение кодах ошибок.
Список исключений API см. в разделе Машинное обучение коды ошибок REST API.