Примечание
Для доступа к этой странице требуется авторизация. Вы можете попробовать войти или изменить каталоги.
Для доступа к этой странице требуется авторизация. Вы можете попробовать изменить каталоги.
Важно!
Поддержка Студии машинного обучения (классической) будет прекращена 31 августа 2024 г. До этой даты рекомендуется перейти на Машинное обучение Azure.
Начиная с 1 декабря 2021 года вы не сможете создавать новые ресурсы Студии машинного обучения (классической). Существующие ресурсы Студии машинного обучения (классическая версия) можно будет использовать до 31 августа 2024 г.
- См. сведения о перемещении проектов машинного обучения из ML Studio (классической) в Машинное обучение Azure.
- См. дополнительные сведения о Машинном обучении Azure.
Поддержка документации по ML Studio (классической) прекращается, а сама документация может не обновляться в будущем.
Интегрирует указанную функцию распределения вероятностей в набор данных
Категория: статистические функции
Примечание
Область применения: только Машинное обучение Studio (классическая версия)
Подобные модули перетаскивания доступны в конструкторе машинного обучения Azure.
Обзор модуля
В этой статье описывается, как использовать модуль функции оценки вероятности в Машинное обучение Studio (классическая модель), чтобы вычислить статистические меры, описывающие распределение столбцов, такие как распределения Бернулли, Парето или Пуассон.
Чтобы использовать эту модель, подключите набор данных, содержащий по крайней мере один столбец числовых значений, и выберите распределение вероятностей для тестирования. Модуль возвращает таблицу данных, содержащую значения из указанной функции вероятности.
Вы можете вычислить любое из этих значений для выбранного распределения вероятности:
- интегральная функция распределения (cdf)
- функция обратного интегрального распределения (InverseCdf)
- функция плотности вероятности (PDF)
Почему распределение вероятностей полезно?
При оценке данных по распределению вероятностей вы сопоставляете значения столбцов с набором значений с известными свойствами. Зная, соответствуют ли данные одному из этих известных дистрибутивов, вы можете определить другие свойства данных. Как правило, можно получить лучшие прогнозы по модели, если определить распределение, которое наилучшим образом подходит для данных.
Выбор функции распределения вероятностей зависит от измеряемых данных и переменных. Например, некоторые распределения предназначены для описания вероятностей дискретных значений; другие предназначены для использования только с непрерывными числовыми переменными. Для некоторых распределений, вы также должны знать заранее ожидаемое среднее, степень свободы и т. д. Дополнительные сведения см. в разделе "Поддерживаемые распределения вероятностей"
Настройка функции оценки вероятности
Все параметры изменяются в зависимости от типа распределения вероятностей, который требуется вычислить. При изменении метода распределения вероятности могут быть сброшены другие выбранные параметры.
Поэтому сначала выберите вариант распространения .
Набор данных, используемый в качестве входных данных, должен содержать числовые данные. Другие типы данных игнорируются.
Для каждого анализа можно применить один метод распределения вероятности. Чтобы вычислить другое распределение вероятности, добавьте отдельный экземпляр модуля для каждого распределения, который планируется протестировать.
Добавьте модуль функции оценки вероятности в эксперимент. Этот модуль можно найти в категории статистических функций в Машинное обучение Studio (классическая модель).
Подключение набор данных, содержащий по крайней мере один столбец чисел.
Используйте параметр распределения, чтобы выбрать тип распределения вероятности, который требуется вычислить. Список параметров и их обязательных аргументов см. в разделе "Поддерживаемые распределения вероятностей ".
Задайте любые параметры, необходимые для распределения.
Выберите одну из трех статистик для создания: интегральная функция распределения (cdf), обратная интегральная функция распределения (InverseCdf) или функция плотности вероятности (pdf).
Сведения об определениях см. в разделе "Технические примечания".
Используйте селектор столбцов, чтобы выбрать столбцы, по которым вычисляется выбранное распределение вероятностей.
Все столбцы, которые вы выбираете, должны иметь числовый тип данных.
Диапазон данных в столбце также должен быть допустимым, с учетом выбранной функции вероятности. В противном случае может возникнуть ошибка или будет получен результат NaN.
Для разреженных столбцов не будут обрабатываться любые значения, которые соответствуют фоновым нулям.
Используйте параметр "Режим результата ", чтобы указать способ вывода результатов. Вы можете заменить значения столбцов значениями распределения вероятностей, добавить новые значения в набор данных или возвратить только значения распределения вероятностей.
Запустите эксперимент или щелкните правой кнопкой мыши модуль функции оценки вероятности и выберите команду "Выполнить".
Результаты
В следующей таблице приведен пример результатов с помощью параметра "Добавить " в одном столбце температуры из примера набора данных "Лесные пожары ".
| temp | StandardNormal.Cdf(temp) | StandardNormal.Pdf(temp) | FFisher.cdf(temp | FFisher.cdf(temp |
|---|---|---|---|---|
| 8.2 | 1 | 1 | 0.984774 | 0.004349 |
| 18 | 1 | 1 | 0.997896 | 0.000311 |
| 14.6 | 1 | 1 | 0.996352 | 0.000648 |
| 8.3 | 1 | 1 | 0.985201 | 0.004187 |
| 11,4 | 1 | 1 | 0.993147 | 0.001502 |
Заголовки созданных столбцов содержат используемое распределение вероятностей.
Если вы не уверены, какое распределение вероятности будет соответствовать вашим данным, можно создать быструю диаграмму совокупного распределения и плотности вероятности для любого числового столбца.
- Щелкните правой кнопкой мыши выходные данные набора данных или модуля и выберите "Визуализировать".
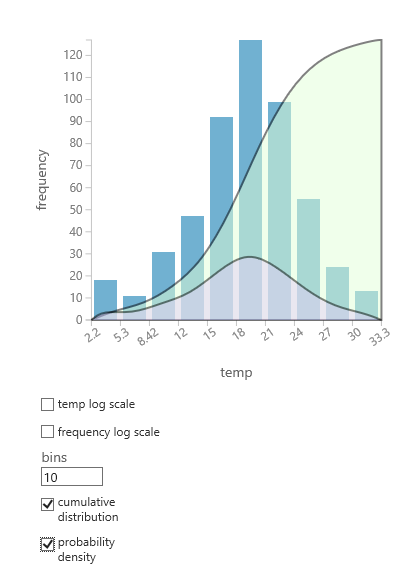
- Выберите интересующий столбец и на панели гистограммы выберите совокупное распределение или плотность вероятности.
- Диаграмма распределения, как показано ниже, накладывается на гистограмму, представляющую данные.
Поддерживаемые распределения вероятностей
Модуль функции оценки вероятности поддерживает следующие распределения:
Bernoulli
Распределение Bernoulli — это распределение по двоичным значениям: другими словами, оно моделирует ожидаемое распределение, если возможны только два значения.
Чтобы вычислить, выберите Bernoulli и задайте следующие параметры:
- Вероятность успеха
Параметр p указывает вероятность создания 1. Введите число (float) в диапазоне от 0,0 до 1,0, которое обозначает вероятность успешного исхода. Значение по умолчанию — 5.
Бета-версия
Бета-распределение — это непрерывное одномерное распределение.
Чтобы вычислить, выбрать бета-версию и задать следующие параметры:
Фигура
Введите значение, чтобы изменить форму распределения.Параметр формы — это любой параметр распределения вероятностей, который не определяет ее расположение или масштаб. Таким образом, при вводе значения формы параметр изменяет форму распределения, а не перемещает, растягивает или сжимает его.
Значение должно быть числом (
double). Значение по умолчанию — 1.0.Масштабирование
Введите число для масштабирования распределения.Применив значение масштаба к распределению, можно сжать или растянуть его.
Значение по умолчанию — 1,0. Значения должны быть положительными числами.
Верхняя граница
Введите число (double), которое представляет собой верхнюю границу распределения. Значение по умолчанию — 1.0.Нижняя граница
Введите число (double), которое представляет собой нижнюю границу распределения. Значение по умолчанию — 0,0.
Binomial
Биномиальное распределение является дискретным однопараментным распределением. Биномиальное распределение используется для моделирования числа успешных исходов в выборке. Замена используется при выборке данных. Для выполнения выборки без замены используйте гипергеометрическое распределение.
Чтобы вычислить, выберите Binomial и задайте следующие параметры:
Вероятность успеха
Введите число (float) в диапазоне от 0,0 до 1,0, которое обозначает вероятность успешного исхода. Значение по умолчанию — 5.Количество попыток
Укажите количество испытаний.Используйте значение
integerс минимальным значением 1. По умолчанию используется значение 3.
Cauchy
Распределение Коши — это симметричное непрерывное распределение вероятности.
Чтобы вычислить, выберите Cauchy и задайте следующие параметры:
Расположение
Введите число (double), представляющее расположение0-го элемента.Указав значение для параметра Расположение, вы можете переместить распределение вероятностей вверх или вниз по цифровой шкале.
Значение по умолчанию — 0,0.
ChiSquare
Распределение чи-квадрат — это сумма квадратов k независимых, стандартных, нормальных, случайных переменных.
Чтобы вычислить, выберите ChiSquare и задайте следующие параметры:
- Количество степеней свободы Введите число (
double), чтобы указать степень свободы. Значение по умолчанию — 1.0.
ChiSquareRightTailed
Этот параметр обеспечивает правостороннее распределение чи-квадратов.
Чтобы вычислить, выберите ChiSquareRightTailed и задайте следующие параметры:
- Количество степеней свободы
Введите число (double), чтобы указать количество степеней свободы. Значение по умолчанию — 1.0.
Экспоненциально
Экспоненциальное распределение — это распределение вещественных чисел, параметризованное по одному неотрицательному параметру.
Чтобы вычислить, выберите экспоненциальное значение и задайте следующие параметры:
- Lambda
Введите число (double), чтобы использовать параметр "Лямбда". Значение по умолчанию — 1.0.
FFisher
Создает вероятность статистики Фишера для выборки, также известной как распределение фишера F.. Это распределение с двумя хвостами.
Чтобы вычислить, выберите FFisher и задайте следующие параметры:
Степени свободы числителя
Введите число (double), чтобы указать степени свободы, используемые в числителе. Значение по умолчанию — 3.0.Множитель степеней свободы
Введите число (double), чтобы указать степени свободы, используемые в знаменателе. Значение по умолчанию — 6.0.
FFisherRightTailed
Создает правостороннее распределение Фишера. Распределение Фишера также называется F-распределением Фишера, распределением Снедекора или распределением Фишера-Снедекора. Данная форма распределения является правосторонней.
Чтобы вычислить, выберите FFisherRightTailed и задайте следующие параметры:
Степени свободы числителя
Введите число (double), чтобы указать степени свободы, используемые в числителе. Значение по умолчанию — 3.0.Множитель степеней свободы
Введите число (double), чтобы указать степени свободы, используемые в знаменателе. Значение по умолчанию — 6.0.
Gamma
Гамма-распределение — это семейство непрерывных распределений вероятностей с двумя параметрами. Например, хи-квадрат представляет собой особый случай гамма-распределения.
Чтобы вычислить, выбрать Гамма и задать следующие параметры:
Масштабирование
Введите значение для масштабирования распределения.Применив значение масштаба к распределению, можно сжать или растянуть его.
Значение по умолчанию — 1,0. Значения должны быть положительными числами.
Расположение
Введите число (double), представляющее расположение0-го элемента.Указав значение для параметра Расположение, вы можете переместить распределение вероятностей вверх или вниз по цифровой шкале.
Значение по умолчанию — 0,0.
GeneralizedExtremeValues
Создает распределение, разработанное для обработки экстремальных значений. Обобщенное распределение экстремальных значений (GEV) — это группа непрерывных распределений вероятностей, которая объединяет в себе распределения Гумбеля, Фреше и Вейбулла (также известных как распределения экстремальных значений типа I, II и III).
Дополнительные сведения об теории экстремальных ценностей см. в этой статье в Википедии: Фишер-Tippet-Gnedenko теорема.
Чтобы вычислить, выберите GeneralizedValues и задайте следующие параметры:
Фигура
Введите значение, чтобы изменить форму распределения.Параметр формы — это любой параметр распределения вероятностей, который не определяет ее расположение или масштаб. Таким образом, при вводе значения формы параметр изменяет форму распределения, а не перемещает, растягивает или сжимает его.
Значение должно быть числом (
double). Значение по умолчанию — 1.0.Масштабирование
Введите значение для масштабирования распределения.Применив значение масштаба к распределению, можно сжать или растянуть его.
Значение по умолчанию — 1,0. Значения должны быть положительными числами.
Расположение
Введите число (double), представляющее расположение0-го элемента.Указав значение для параметра Расположение, вы можете сместить распределение вероятностей вверх или вниз по цифровой шкале.
Значение по умолчанию — 0,0.
Геометрический
Геометрическое распределение — это распределение по положительным целым числам, параметризованным одним положительным реальным числом.
Чтобы вычислить, выбрать "Геометрическая" и задать следующие параметры:
- Вероятность успеха
Введите число (float) в диапазоне от 0,0 до 1,0, которое обозначает вероятность успешного исхода. Значение по умолчанию — .5.
Примечание
Эта реализация геометрического распределения не создает нули.
GumbelMax
Распределение Гумбеля является одним из нескольких распределений экстремальных значений. В этом варианте GumbelMax реализуется распределение наибольших экстремальных значений типа 1.
Чтобы вычислить, выберите GumbelMax и задайте следующие параметры:
Масштабирование
Введите значение для масштабирования распределения.Применив значение масштаба к распределению, можно сжать или растянуть его.
Значение по умолчанию — 1,0. Значения должны быть положительными числами.
Расположение
Введите число (double), представляющее расположение0-го элемента.Указав значение для параметра Расположение, вы можете сместить распределение вероятностей вверх или вниз по цифровой шкале.
Значение по умолчанию — 0,0.
GumbelMin
Распределение Гумбеля является одним из нескольких распределений экстремальных значений. Распределение Гумбеля также называется распределением наименьших экстремальных значений (SEV) или распределением наименьших экстремальных значений (тип I). Параметр GumbelMin реализует распределение минимального крайнего значения 1.
Чтобы вычислить, выберите GumbelMin и задайте следующие параметры:
Масштабирование
Введите значение для масштабирования распределения.Применив значение масштаба к распределению, можно сжать или растянуть его.
Значение по умолчанию — 1,0. Значения должны быть положительными числами.
Расположение
Введите число (double), представляющее расположение0-го элемента.Указав значение для параметра Расположение, вы можете сместить распределение вероятностей вверх или вниз по цифровой шкале.
Значение по умолчанию — 0,0.
Hypergeometric
Гипергеометрическое распределение — это дискретное распределение вероятности, описывающее количество успешных операций в последовательности n, полученных из конечной совокупности без замены, так же, как биномиальное распределение описывает количество успешных операций для рисования с заменой.
Чтобы вычислить, выберите Hypergeometric и задайте следующие параметры:
Число выборок
Введите целое число, указывающее количество используемых выборок. Значение по умолчанию — 9.Количество успешных исходов
Введите целое число, определяющее значение для достижения успеха. Значение по умолчанию — 24.Размер совокупности
Укажите размер совокупности для использования при оценке гипергеометрического распределения.
Лапласовский
Распределение Laplace — это распределение по реальным числам, параметризуемое средним и масштабируемым параметром.
Чтобы вычислить, выберите распределение Laplace и задайте следующие параметры:
Масштабирование
Введите значение для масштабирования распределения.Применив значение масштаба к распределению, можно сжать или растянуть его.
Значение по умолчанию — 1,0. Значения должны быть положительными числами.
Расположение
Введите число (double), представляющее расположение0-го элемента.Указав значение для параметра Расположение, вы можете сместить распределение вероятностей вверх или вниз по цифровой шкале.
Значение по умолчанию — 0,0.
Логарифмический
Логистическое распределение аналогично нормальному распределению, но оно не имеет ограничения по левой стороне распределения. Логистическое распределение используется в модели нейронной сети и логистической регрессии, а также для моделирования данных естественных наук.
Чтобы вычислить, выбрать "Логистика" и задать следующие параметры:
Масштабирование
Введите значение для масштабирования распределения.Применив значение масштаба к распределению, можно сжать или растянуть его.
Значение по умолчанию — 1,0. Значения должны быть положительными числами.
Среднее
Введите число (double), которое указывает расчетное среднее значение распределения. Значение по умолчанию — 0,0.
Lognormal
Логарифмически нормальное распределение — это непрерывное одномерное распределение.
Чтобы вычислить, выберите Lognormal и задайте следующие параметры:
Среднее
Введите число (double), указывающее предполагаемое среднее значение распределения. Значение по умолчанию — 0,0.Стандартное отклонение
Введите положительное число (double), которое указывает расчетное стандартное отклонение для распределения. Значение по умолчанию — 1.0.
NegativeBinomial
Отрицательное биномиальное распределение — это распределение по натуральным числам с двумя параметрами (r, p). В особом случае, которое r является целым числом, можно интерпретировать распределение как число хвостовперед головой r, когда вероятность головы составляет p.
Чтобы вычислить, выберите NegativeBinomial и задайте следующие параметры:
Вероятность успеха
Введите число (float) в диапазоне от 0,0 до 1,0, которое обозначает вероятность успешного исхода. Значение по умолчанию — .5.Количество успешных исходов
Введите целое число, указывающее значение для достижения успеха. Значение по умолчанию — 24.
Норм.
Обычное распределение также называется гаусским распределением.
Чтобы вычислить, выбрать "Обычный" и задать следующие параметры:
Среднее
Введите число (double), указывающее предполагаемое среднее значение распределения. Значение по умолчанию — 0,0.Стандартное отклонение
Введите положительное число (double), которое указывает расчетное стандартное отклонение для распределения. Значение по умолчанию — 1.0.
Pareto
Распределение Парето — это распределение вероятностей по степенному закону, которое встречается при исследовании социальных, научных, геофизических, страховых и многих других типов явлений.
Чтобы вычислить, выберите Pareto и задайте следующие параметры:
Фигура
Введите значение (необязательно), чтобы изменить форму распределения.Параметр формы — это любой параметр распределения вероятностей, который не определяет ее расположение или масштаб. Таким образом, при вводе значения формы параметр изменяет форму распределения, а не перемещает, растягивает или сжимает его.
Значение должно быть числом (
double). Значение по умолчанию — 1.0.Масштабирование
Введите значение (необязательно), чтобы изменить масштаб распределения. Применив значение масштаба к распределению, можно сжать или растянуть его.Значение должно быть числом (
double). Значение по умолчанию — 1.0.
Poisson
В этой реализации метод Кнута используется для создания распределенных случайных переменных Пуассона. Дополнительные сведения о распределении Poisson см. в разделе "Регрессия Poisson".
Чтобы вычислить, выберите Poisson и задайте следующие параметры:
- Среднее
Введите число (double), указывающее предполагаемое среднее значение распределения. Значение по умолчанию — 0,0.
Rayleigh
Распределение Релея — это непрерывное распределение вероятности. Пример возникновения распределения: скорость ветра имеет распределение Рэлея, если компоненты двухмерного вектора скорости ветра некоррелированы и нормально распределены с равной дисперсией.
Чтобы вычислить, выберите Rayleigh и задайте следующие параметры:
- Нижняя граница
Введите число (double), которое представляет собой нижнюю границу распределения. Значение по умолчанию — 0,0.
StandardNormal
Этот параметр обеспечивает стандартное нормальное распределение без других параметров.
Чтобы вычислить, выберите StandardNormal и выберите столбцы.
TStudent
Этот параметр реализует однопараметрическое распределение student.
Чтобы вычислить, выберите TStudent и задайте следующие параметры:
- Количество степеней свободы
Введите число (double), чтобы указать количество степеней свободы. Значение по умолчанию — 1.0.
TStudentRightTailed
Реализует одномерное T-распределение Стьюдента с использованием одной правой стороны.
Чтобы вычислить, выберите TStudentRightTailed и задайте следующие параметры:
- Количество степеней свободы
Введите число (double), чтобы указать количество степеней свободы. Значение по умолчанию — 1.0.
TStudentTwoTailed
Реализует двустороннее T-распределение Стьюдента.
Чтобы вычислить, выберите TStudentTwoTailed и задайте следующие параметры:
- Количество степеней свободы
Введите число (double), чтобы указать количество степеней свободы. Значение по умолчанию — 1.0.
Равномерное
Равномерное распределение также называется прямоугольным распределением.
Чтобы вычислить, выбрать "Единообразие" и задать следующие параметры:
Нижняя граница
Введите число (double), которое представляет собой нижнюю границу распределения. Значение по умолчанию — 0,0.Верхняя граница
Введите число (double), которое представляет собой верхнюю границу распределения. Значение по умолчанию — 1.0.
Weibull
Распределение Вейбулла широко используется в техническом обеспечении надежности. Его параметр Shape можно использовать для моделирования многих других распределений.
Чтобы вычислить, выберите Weibull и задайте следующие параметры:
Фигура
Введите значение (необязательно), чтобы изменить форму распределения.Параметр формы — это любой параметр распределения вероятностей, который не определяет ее расположение или масштаб. Таким образом, при вводе значения формы параметр изменяет форму распределения, а не перемещает, растягивает или сжимает его.
Значение должно быть числом (
double). Значение по умолчанию — 1.0.Масштабирование
Введите значение (необязательно), чтобы изменить масштаб распределения. Применив значение масштаба к распределению, можно сжать или растянуть его.Значение должно быть числом (
double). Значение по умолчанию — 1.0.
Технические примечания
В этом разделе содержатся сведения о реализации, советы и ответы на часто задаваемые вопросы.
Сведения о реализации
Этот модуль поддерживает все распределения, представленные в библиотеке числовых значений MATH.Net с открытым исходным кодом. Дополнительные сведения см. в документации по библиотеке Math.Net.Numerics.Distribution .
Правостороннее и двухстороннее распределение отображаются как отдельные дистрибутивы, а не как параметризованные версии базовых дистрибутивов. Текущее поведение — сохранение совместимости с Excel.
Определения
Этот модуль поддерживает вычисление любого из этих значений для указанного распределения:
cdf или интегральная функция распределения
Возвращает вероятность составного события, определенную как сумма ocurrences, когда случайная переменная принимает значение меньше определенного значения x.
Другими словами, он отвечает на вопрос: "Насколько распространены примеры, которые меньше или равны этому значению?"
Эту функцию можно использовать как с непрерывными, так и дискретными числовыми переменными.
InverseCdf или обратная интегральная функция распределения
Возвращает значение, связанное с определенным совокупным значением вероятности (cdf).
Другими словами, он отвечает на вопрос: "Какое значение x, в котором функция cdf возвращает интегральную вероятность y?"
pdf или функция плотности вероятности
Описывает относительную вероятность того, что случайная переменная является конкретным значением.
Другими словами, он отвечает на вопрос: "Насколько часто примеры имеют именно это значение?"
Ожидаемые входные данные
| Имя | Тип | Описание |
|---|---|---|
| Dataset | Таблица данных | Входной набор данных |
Параметры модуля
| Имя | Диапазон | Тип | По умолчанию | Описание |
|---|---|---|---|---|
| Distribution | Любой | ProbabilityDistribution | StandardNormal | Выберите тип создаваемого распределения вероятностей. |
| Метод | Любой | ProbabilityDistributionMethod | Cdf | Выберите метод вычисления выбранного распределения вероятностей. Доступны такие параметры, как кумулятивная функция распределения (cdf), обратная кумулятивная функция распределения (InverseCdf) и функция плотности (или массы) вероятности (pdf). |
| Метод отрицательного биномиального распределения | Любой | ProbabilityDistributionMethodForNegativeBinomial | Cdf | При выборе отрицательного биномиального распределения следует указать метод оценки распределения. |
| Вероятность успеха | [0.0;1.0] | Float | 0,5 | Введите значение, используемое в качестве вероятности успеха. |
| Фигура | Любой | Float | 1.0 | Введите значение, которое изменит форму распределения. |
| Масштабирование | >=0,0 | Float | 1.0 | Введите значение, изменяющее масштаб распределения, чтобы увеличить или уменьшить его размер. |
| Количество попыток | >=1 | Целочисленный тип | 3 | Укажите количество испытаний. |
| Нижняя граница | Любой | Float | 0,0 | Введите число, которое будет использоваться в качестве нижней границы распределения. |
| Верхняя граница | Любой | Float | 1.0 | Введите число, которое будет использоваться в качестве верхней границы распределения. |
| Расположение | Любой | Float | 0,0 | Введите расположение нулевого элемента в распределении. |
| Количество степеней свободы | Любой | Float | 1.0 | Укажите число степеней свободы. |
| Степени свободы числителя | Любой | Float | 3.0 | Укажите число степеней свободы в числителе. |
| Множитель степеней свободы | Любой | Float | 6,0 | Укажите число степеней свободы в множителе. |
| Lambda | >=0,0 | Float | 1.0 | Укажите значение для параметра "Лямбда". |
| Число выборок | Любой | Целое число | 9 | Укажите количество выборок. |
| Количество успешных исходов | Любой | Целое число | 24 | Введите значение, используемое в качестве количества успешных исходов. |
| Размер совокупности | Любой | Целое число | 52 | Укажите размер совокупности. |
| Среднее значение | Любой | Float | 0,0 | Введите расчетное среднее значение. |
| Standard deviation | >=0,0 | Float | 1.0 | Введите расчетное стандартное отклонение. |
| Набор столбцов | Любой | Выбор столбцов | Выберите столбцы, для которых вычисляется распределение вероятности. | |
| Режим «Результат» | Любой | OutputTo | ResultOnly | Укажите, как следует сохранять результаты в выходном наборе данных. Возможные варианты: добавить новые столбцы, заменить существующие столбцы или вывести только результаты. |
Выходные данные
| Имя | Тип | Описание |
|---|---|---|
| Набор данных результатов | Таблица данных | Выходной набор данных |
Исключение
Полный список сообщений об ошибках см. в разделе "Коды ошибок модуля".
| Исключение | Описание |
|---|---|
| Ошибка 0017 | Исключение возникает, если один или несколько указанных столбцов относятся к типу, который не поддерживается в текущем модуле. |
Список ошибок, относящихся к модулям Студии (классическая модель), см. в Машинное обучение кодах ошибок.
Список исключений API см. в разделе Машинное обучение коды ошибок REST API.