Transformações não afins
Criar efeitos de perspectiva e conicidade com a terceira coluna da matriz de transformação
Translação, escala, rotação e inclinação são todas classificadas como transformadas afim . As transformadas afins preservam linhas paralelas. Se duas linhas são paralelas antes da transformação, elas permanecem paralelas após a transformação. Os retângulos são sempre transformados em paralelogramos.
No entanto, SkiaSharp também é capaz de transformações não-afim, que têm a capacidade de transformar um retângulo em qualquer quadrilátero convexo:

Um quadrilátero convexo é uma figura de quatro lados com ângulos interiores sempre inferiores a 180 graus e lados que não se cruzam.
As transformações não afins resultam quando a terceira linha da matriz de transformação é definida como valores diferentes de 0, 0 e 1. A multiplicação completa SKMatrix é:
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z' |
│ TransX TransY Persp2 │
As fórmulas de transformação resultantes são:
x' = ScaleX·x + SkewX·y + TransX
y' = SkewY·x + ScaleY·y + TransY
z' = Persp0·x + Persp1·y + Persp2
A regra fundamental de usar uma matriz 3 por 3 para transformações bidimensionais é que tudo permanece no plano onde Z é igual a 1. A menos que Persp0 e Persp1 sejam 0, e Persp2 seja igual a 1, a transformação moveu as coordenadas Z para fora desse plano.
Para restaurar isso para uma transformação bidimensional, as coordenadas devem ser movidas de volta para esse plano. Mais um passo é necessário. Os valores x', y' e z' devem ser divididos por z':
x" = x' / z'
y" = y' / z'
z" = z' / z' = 1
Estas são conhecidas como coordenadas homogêneas e foram desenvolvidas pelo matemático August Ferdinand Möbius, muito mais conhecido por sua estranheza topológica, a Faixa de Möbius.
Se z' é 0, a divisão resulta em coordenadas infinitas. De fato, uma das motivações de Möbius para o desenvolvimento de coordenadas homogêneas foi a capacidade de representar valores infinitos com números finitos.
Ao exibir gráficos, no entanto, você deseja evitar renderizar algo com coordenadas que se transformam em valores infinitos. Essas coordenadas não serão renderizadas. Tudo nas proximidades dessas coordenadas será muito grande e provavelmente não será visualmente coerente.
Nesta equação, você não quer que o valor de z' se torne zero:
z' = Persp0·x + Persp1·y + Persp2
Consequentemente, esses valores têm algumas restrições práticas:
A Persp2 célula pode ser zero ou não zero. Se Persp2 é zero, então z' é zero para o ponto (0, 0), e isso geralmente não é desejável porque esse ponto é muito comum em gráficos bidimensionais. Se Persp2 não for igual a zero, então não há perda de generalidade se Persp2 for fixado em 1. Por exemplo, se você determinar que Persp2 deve ser 5, então você pode simplesmente dividir todas as células na matriz por 5, o que faz Persp2 igual a 1, e o resultado será o mesmo.
Por essas razões, Persp2 muitas vezes é fixado em 1, que é o mesmo valor na matriz de identidade.
Geralmente, Persp0 e Persp1 são números pequenos. Por exemplo, suponha que você comece com uma matriz de identidade, mas defina Persp0 como 0,01:
| 1 0 0.01 | | 0 1 0 | | 0 0 1 |
As fórmulas de transformação são:
x' = x / (0,01·x + 1)
y' = y / (0,01·x + 1)
Agora use essa transformação para renderizar uma caixa quadrada de 100 pixels posicionada na origem. Veja como os quatro cantos são transformados:
(0, 0) → (0, 0)
(0, 100) → (0, 100)
(100, 0) → (50, 0)
(100, 100) → (50, 50)
Quando x é 100, então o denominador z' é 2, então as coordenadas x e y são efetivamente reduzidas pela metade. O lado direito da caixa torna-se mais curto do que o lado esquerdo:
A Persp parte desses nomes de célula refere-se a "perspectiva" porque o encurtamento sugere que a caixa agora está inclinada com o lado direito mais distante do visualizador.
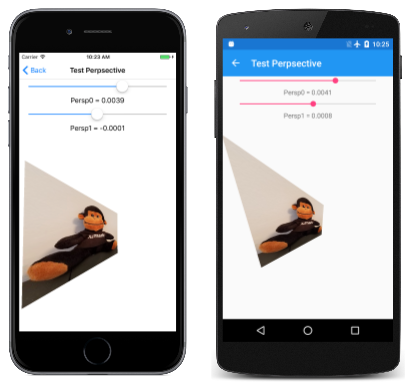
A página Perspectiva de teste permite que você experimente valores de e Pers1 tenha uma ideia de Persp0 como eles funcionam. Os valores razoáveis dessas células de matriz são tão pequenos que a Slider na Plataforma Universal do Windows não pode manipulá-los adequadamente. Para acomodar o problema da UWP, os dois Slider elementos no TestPerspective.xaml precisam ser inicializados para variar de –1 a 1:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.TestPerspectivePage"
Title="Test Perpsective">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Minimum" Value="-1" />
<Setter Property="Maximum" Value="1" />
<Setter Property="Margin" Value="20, 0" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="persp0Slider"
Grid.Row="0"
ValueChanged="OnPersp0SliderValueChanged" />
<Label x:Name="persp0Label"
Text="Persp0 = 0.0000"
Grid.Row="1" />
<Slider x:Name="persp1Slider"
Grid.Row="2"
ValueChanged="OnPersp1SliderValueChanged" />
<Label x:Name="persp1Label"
Text="Persp1 = 0.0000"
Grid.Row="3" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="4"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Os manipuladores de eventos para os controles deslizantes no TestPerspectivePage arquivo code-behind dividem os valores por 100 para que eles variem entre –0,01 e 0,01. Além disso, o construtor carrega em um bitmap:
public partial class TestPerspectivePage : ContentPage
{
SKBitmap bitmap;
public TestPerspectivePage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnPersp0SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp0Label.Text = String.Format("Persp0 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
void OnPersp1SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp1Label.Text = String.Format("Persp1 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
...
}
O PaintSurface manipulador calcula um SKMatrix valor nomeado perspectiveMatrix com base nos valores desses dois controles deslizantes divididos por 100. Isso é combinado com duas transformações de conversão que colocam o centro dessa transformação no centro do bitmap:
public partial class TestPerspectivePage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Calculate perspective matrix
SKMatrix perspectiveMatrix = SKMatrix.MakeIdentity();
perspectiveMatrix.Persp0 = (float)persp0Slider.Value / 100;
perspectiveMatrix.Persp1 = (float)persp1Slider.Value / 100;
// Center of screen
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
SKMatrix.PostConcat(ref matrix, perspectiveMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(xCenter, yCenter));
// Coordinates to center bitmap on canvas
float x = xCenter - bitmap.Width / 2;
float y = yCenter - bitmap.Height / 2;
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
}
Aqui estão algumas imagens de exemplo:
Ao experimentar os controles deslizantes, você descobrirá que valores além de 0,0066 ou abaixo de –0,0066 fazem com que a imagem se torne subitamente fraturada e incoerente. O bitmap que está sendo transformado é quadrado de 300 pixels. Ele é transformado em relação ao seu centro, de modo que as coordenadas do bitmap variam de –150 a 150. Lembre-se que o valor de z' é:
z' = Persp0·x + Persp1·y + 1
Se Persp0 ou Persp1 for maior que 0,0066 ou menor que –0,0066, sempre haverá alguma coordenada do bitmap que resulte em um valor z' de zero. Isso causa divisão por zero, e a renderização se torna uma bagunça. Ao usar transformações não afim, você deseja evitar renderizar qualquer coisa com coordenadas que causem divisão por zero.
Geralmente, você não estará definindo Persp0 e Persp1 isoladamente. Muitas vezes também é necessário colocar outras células na matriz para alcançar certos tipos de transformações não afim.
Uma dessas transformadas não afins é uma transformada de cone. Este tipo de transformada não afim retém as dimensões gerais de um retângulo, mas afina um lado:
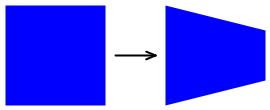
A TaperTransform classe executa um cálculo generalizado de uma transformada não afim com base nestes parâmetros:
- o tamanho retangular da imagem que está sendo transformada,
- uma enumeração que indica o lado do retângulo que diminui,
- outra enumeração que indica como ele diminui, e
- a extensão do tapering.
Este é o código :
enum TaperSide { Left, Top, Right, Bottom }
enum TaperCorner { LeftOrTop, RightOrBottom, Both }
static class TaperTransform
{
public static SKMatrix Make(SKSize size, TaperSide taperSide, TaperCorner taperCorner, float taperFraction)
{
SKMatrix matrix = SKMatrix.MakeIdentity();
switch (taperSide)
{
case TaperSide.Left:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp0 = (taperFraction - 1) / size.Width;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Top:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp1 = (taperFraction - 1) / size.Height;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Right:
matrix.ScaleX = 1 / taperFraction;
matrix.Persp0 = (1 - taperFraction) / (size.Width * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
break;
}
break;
case TaperSide.Bottom:
matrix.ScaleY = 1 / taperFraction;
matrix.Persp1 = (1 - taperFraction) / (size.Height * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
break;
}
break;
}
return matrix;
}
}
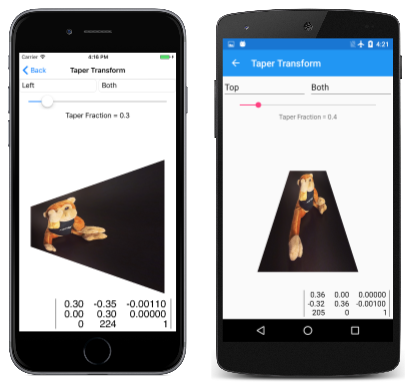
Essa classe é usada na página Transformação de cone . O arquivo XAML instancia dois Picker elementos para selecionar os valores de enumeração e um Slider para escolher a fração de cone. O PaintSurface manipulador combina a transformação de conicidade com duas transformações de conversão para tornar a transformação relativa ao canto superior esquerdo do bitmap:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
TaperSide taperSide = (TaperSide)taperSidePicker.SelectedItem;
TaperCorner taperCorner = (TaperCorner)taperCornerPicker.SelectedItem;
float taperFraction = (float)taperFractionSlider.Value;
SKMatrix taperMatrix =
TaperTransform.Make(new SKSize(bitmap.Width, bitmap.Height),
taperSide, taperCorner, taperFraction);
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(taperMatrix);
matrixDisplay.Paint(canvas, taperMatrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Center bitmap on canvas
float x = (info.Width - bitmap.Width) / 2;
float y = (info.Height - bitmap.Height) / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-x, -y);
SKMatrix.PostConcat(ref matrix, taperMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(x, y));
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
Estes são alguns exemplos:
Outro tipo de transformadas não afins generalizadas é a rotação 3D, que é demonstrada no próximo artigo, Rotações 3D.
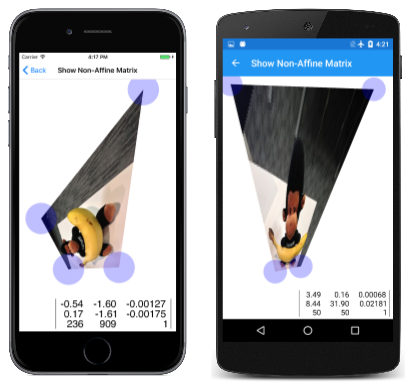
A transformada não afim pode transformar um retângulo em qualquer quadrilátero convexo. Isso é demonstrado pela página Mostrar matriz não afim. É muito semelhante à página Mostrar Matriz Afim do artigo Transformações de Matriz, exceto que ela tem um quarto TouchPoint objeto para manipular o quarto canto do bitmap:
Contanto que você não tente fazer um ângulo interior de um dos cantos do bitmap maior que 180 graus, ou fazer dois lados se cruzarem, o programa calcula com êxito a transformação usando este método da ShowNonAffineMatrixPage classe:
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL, SKPoint ptLR)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
// Non-Affine transform
SKMatrix inverseA;
A.TryInvert(out inverseA);
SKPoint abPoint = inverseA.MapPoint(ptLR);
float a = abPoint.X;
float b = abPoint.Y;
float scaleX = a / (a + b - 1);
float scaleY = b / (a + b - 1);
SKMatrix N = new SKMatrix
{
ScaleX = scaleX,
ScaleY = scaleY,
Persp0 = scaleX - 1,
Persp1 = scaleY - 1,
Persp2 = 1
};
// Multiply S * N * A
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.PostConcat(ref result, S);
SKMatrix.PostConcat(ref result, N);
SKMatrix.PostConcat(ref result, A);
return result;
}
Para facilitar o cálculo, esse método obtém a transformação total como um produto de três transformações separadas, que são simbolizadas aqui com setas mostrando como essas transformações modificam os quatro cantos do bitmap:
(0, 0) → (0, 0) → (0, 0) → (x0, y0) (canto superior esquerdo)
(0, H) → (0, 1) → (0, 1) → (x1, y1) (canto inferior esquerdo)
(W, 0) → (1, 0) → (1, 0) → (x2, y2) (canto superior direito)
(W, H) → (1, 1) → (a, b) → (x3, y3) (canto inferior direito)
As coordenadas finais à direita são os quatro pontos associados aos quatro pontos de contato. Essas são as coordenadas finais dos cantos do bitmap.
W e H representam a largura e a altura do bitmap. A primeira transformação S simplesmente dimensiona o bitmap para um quadrado de 1 pixel. A segunda transformada é a transformada Nnão-afim, e a terceira é a transformada Aafim. Essa transformação afim é baseada em três pontos, então é como o método afim ComputeMatrix anterior e não envolve a quarta linha com o ponto (a, b).
Os a valores e b são calculados de modo que a terceira transformação seja afim. O código obtém o inverso da transformação afim e, em seguida, usa isso para mapear o canto inferior direito. Esse é o ponto (a, b).
Outro uso de transformações não-afins é imitar gráficos tridimensionais. No próximo artigo, Rotações 3D você verá como girar um gráfico bidimensional no espaço 3D.