Transformações matriciais no SkiaSharp
Aprofunde-se nas transformações SkiaSharp com a versátil matriz de transformação
Todas as transformações aplicadas ao SKCanvas objeto são consolidadas em uma única instância da SKMatrix estrutura. Esta é uma matriz de transformação 3 por 3 padrão semelhante às de todos os sistemas gráficos 2D modernos.
Como você viu, você pode usar transformações no SkiaSharp sem saber sobre a matriz de transformação, mas a matriz de transformação é importante de uma perspectiva teórica, e é crucial ao usar transformações para modificar caminhos ou para lidar com entradas de toque complexas, ambas demonstradas neste artigo e no próximo.

A matriz de transformação atual aplicada ao SKCanvas está disponível a qualquer momento acessando a propriedade somente TotalMatrix leitura. Você pode definir uma nova matriz de transformação usando o SetMatrix método e pode restaurar essa matriz de transformação para valores padrão chamando ResetMatrix.
O único outro SKCanvas membro que trabalha diretamente com a transformação de matriz da tela é Concat que concatena duas matrizes multiplicando-as juntas.
A matriz de transformação padrão é a matriz de identidade e consiste em 1's nas células diagonais e 0's em todos os outros lugares:
| 1 0 0 | | 0 1 0 | | 0 0 1 |
Você pode criar uma matriz de identidade usando o método estático SKMatrix.MakeIdentity :
SKMatrix matrix = SKMatrix.MakeIdentity();
O SKMatrix construtor padrão não retorna uma matriz de identidade. Ele retorna uma matriz com todas as células definidas como zero. Não use o construtor, a SKMatrix menos que você planeje definir essas células manualmente.
Quando SkiaSharp renderiza um objeto gráfico, cada ponto (x, y) é efetivamente convertido em uma matriz 1 por 3 com um 1 na terceira coluna:
| x y 1 |
Esta matriz 1 por 3 representa um ponto tridimensional com a coordenada Z definida como 1. Existem razões matemáticas (discutidas mais adiante) pelas quais uma transformação de matriz bidimensional requer trabalhar em três dimensões. Você pode pensar nessa matriz 1 por 3 como representando um ponto em um sistema de coordenadas 3D, mas sempre no plano 2D onde Z é igual a 1.
Essa matriz 1 por 3 é então multiplicada pela matriz de transformação, e o resultado é o ponto renderizado na tela:
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
Usando a multiplicação de matriz padrão, os pontos convertidos são os seguintes:
x' = x
y' = y
z' = 1
Essa é a transformação padrão.
Quando o Translate método é chamado no SKCanvas objeto, os tx argumentos e ty para o Translate método tornam-se as duas primeiras células na terceira linha da matriz de transformação:
| 1 0 0 | | 0 1 0 | | tx ty 1 |
A multiplicação agora é a seguinte:
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| tx ty 1 |
Aqui estão as fórmulas de transformação:
x' = x + tx
y' = y + ty
Os fatores de dimensionamento têm um valor padrão de 1. Quando você chama o Scale método em um novo SKCanvas objeto, a matriz de transformação resultante contém os sx argumentos e sy nas células diagonais:
| sx 0 0 |
| x y 1 | × | 0 sy 0 | = | x' y' z' |
| 0 0 1 |
As fórmulas de transformação são as seguintes:
x' = sx · x
y' = sy · y
A matriz de transformação após a chamada Skew contém os dois argumentos nas células da matriz adjacentes aos fatores de escala:
│ 1 ySkew 0 │
| x y 1 | × │ xSkew 1 0 │ = | x' y' z' |
│ 0 0 1 │
As fórmulas de transformação são:
x' = x + xSkew · y
y' = ySkew · x + y
Para uma chamada para RotateDegrees ou RotateRadians para um ângulo de α, a matriz de transformação é a seguinte:
│ cos(α) sin(α) 0 │
| x y 1 | × │ –sin(α) cos(α) 0 │ = | x' y' z' |
│ 0 0 1 │
Aqui estão as fórmulas de transformação:
x' = cos(α) · x - sin(α) · y
y' = sin(α) · x - cos(α) · y
Quando α é 0 graus, é a matriz de identidade. Quando α é de 180 graus, a matriz de transformação é a seguinte:
| –1 0 0 | | 0 –1 0 | | 0 0 1 |
Uma rotação de 180 graus é equivalente a virar um objeto horizontal e verticalmente, o que também é realizado definindo fatores de escala de –1.
Todos esses tipos de transformações são classificados como transformadas afim . As transformações afins nunca envolvem a terceira coluna da matriz, que permanece nos valores padrão de 0, 0 e 1. O artigo Non-Affine Transforms discute as transformações não-afim.
multiplicação de matrizes
Uma vantagem significativa com o uso da matriz de transformação é que as transformadas compostas podem ser obtidas por multiplicação de matriz, que é frequentemente referida na documentação do SkiaSharp como concatenação. Muitos dos métodos relacionados à transformação referem-se SKCanvas a "pré-concatenação" ou "pré-concratação". Isso se refere à ordem de multiplicação, que é importante porque a multiplicação matricial não é comutativa.
Por exemplo, a documentação para o Translate método diz que ele "Pré-concats a matriz atual com a tradução especificada", enquanto a documentação para o Scale método diz que ele "Pré-concats a matriz atual com a escala especificada".
Isso significa que a transformação especificada pela chamada do método é o multiplicador (o operando esquerdo) e a matriz de transformação atual é o multiplicando (o operando direito).
Suponha que Translate seja chamado seguido de Scale:
canvas.Translate(tx, ty);
canvas.Scale(sx, sy);
A Scale transformação é multiplicada pela Translate transformada para a matriz de transformação composta:
| sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | 0 0 1 | | tx ty 1 | | tx ty 1 |
Scale poderia ser chamado antes Translate assim:
canvas.Scale(sx, sy);
canvas.Translate(tx, ty);
Nesse caso, a ordem da multiplicação é invertida e os fatores de escala são efetivamente aplicados aos fatores de tradução:
| 1 0 0 | | sx 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | = | 0 sy 0 | | tx ty 1 | | 0 0 1 | | tx·sx ty·sy 1 |
Aqui está o Scale método com um ponto de pivô:
canvas.Scale(sx, sy, px, py);
Isso é equivalente às seguintes chamadas de tradução e dimensionamento:
canvas.Translate(px, py);
canvas.Scale(sx, sy);
canvas.Translate(–px, –py);
As três matrizes de transformação são multiplicadas em ordem inversa de como os métodos aparecem no código:
| 1 0 0 | | sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | –px –py 1 | | 0 0 1 | | px py 1 | | px–px·sx py–py·sy 1 |
A estrutura do SKMatrix
A SKMatrix estrutura define nove propriedades de leitura/gravação do tipo float correspondentes às nove células da matriz de transformação:
│ ScaleX SkewY Persp0 │ │ SkewX ScaleY Persp1 │ │ TransX TransY Persp2 │
SKMatrix também define uma propriedade chamada Values do tipo float[]. Essa propriedade pode ser usada para definir ou obter os nove valores em um disparo na ordem ScaleX, SkewX, TransX, SkewY, ScaleY, TransY, Persp0, , Persp1e Persp2.
O Persp0, Persp1e Persp2 as células são discutidos no artigo Transformações Não-Afim. Se essas células tiverem seus valores padrão de 0, 0 e 1, a transformação será multiplicada por um ponto de coordenada como este:
│ ScaleX SkewY 0 │
| x y 1 | × │ SkewX ScaleY 0 │ = | x' y' z' |
│ TransX TransY 1 │
x' = ScaleX · x + SkewX · y + TransX
y' = SkewX · x + ScaleY · y + TransY
z' = 1
Esta é a transformada afim bidimensional completa. A transformada afim preserva linhas paralelas, o que significa que um retângulo nunca é transformado em nada além de um paralelogramo.
A SKMatrix estrutura define vários métodos estáticos para criar SKMatrix valores. Todos esses valores retornam SKMatrix :
MakeTranslationMakeScaleMakeScalecom um ponto de pivôMakeRotationpara um ângulo em radianosMakeRotationpara um ângulo em radianos com um ponto de pivôMakeRotationDegreesMakeRotationDegreescom um ponto de pivôMakeSkew
SKMatrix também define vários métodos estáticos que concatenam duas matrizes, o que significa multiplicá-las. Esses métodos são nomeados Concat, PostConcate PreConcat, e há duas versões de cada um. Esses métodos não têm valores de retorno; em vez disso, eles fazem referência a valores existentes SKMatrix por meio de ref argumentos. No exemplo a seguir, A, Be R (para "resultado") são todos os SKMatrix valores.
Os dois Concat métodos são chamados assim:
SKMatrix.Concat(ref R, A, B);
SKMatrix.Concat(ref R, ref A, ref B);
Eles realizam a seguinte multiplicação:
R = B × A
Os outros métodos têm apenas dois parâmetros. O primeiro parâmetro é modificado e, ao retornar da chamada de método, contém o produto das duas matrizes. Os dois PostConcat métodos são chamados assim:
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, ref B);
Essas chamadas executam a seguinte operação:
A = A × B
Os dois PreConcat métodos são semelhantes:
SKMatrix.PreConcat(ref A, B);
SKMatrix.PreConcat(ref A, ref B);
Essas chamadas executam a seguinte operação:
A = B × A
As versões desses métodos com todos os ref argumentos são um pouco mais eficientes em chamar as implementações subjacentes, mas pode ser confuso para alguém lendo seu código e assumindo que qualquer coisa com um ref argumento é modificada pelo método. Além disso, muitas vezes é conveniente passar um argumento que é resultado de um dos Make métodos, por exemplo:
SKMatrix result;
SKMatrix.Concat(result, SKMatrix.MakeTranslation(100, 100),
SKMatrix.MakeScale(3, 3));
Isso cria a seguinte matriz:
│ 3 0 0 │ │ 0 3 0 │ │ 100 100 1 │
Esta é a transformação de escala multiplicada pela transformação de tradução. Nesse caso específico, a SKMatrix estrutura fornece um atalho com um método chamado SetScaleTranslate:
SKMatrix R = new SKMatrix();
R.SetScaleTranslate(3, 3, 100, 100);
Esta é uma das poucas vezes em que é seguro usar o SKMatrix construtor. O SetScaleTranslate método define todas as nove células da matriz. Também é seguro usar o SKMatrix construtor com a estática Rotate e RotateDegrees métodos:
SKMatrix R = new SKMatrix();
SKMatrix.Rotate(ref R, radians);
SKMatrix.Rotate(ref R, radians, px, py);
SKMatrix.RotateDegrees(ref R, degrees);
SKMatrix.RotateDegrees(ref R, degrees, px, py);
Esses métodos não concatenam uma transformação de rotação para uma transformação existente. Os métodos definem todas as células da matriz. Eles são funcionalmente idênticos aos MakeRotation métodos e MakeRotationDegrees , exceto que eles não instanciam o SKMatrix valor.
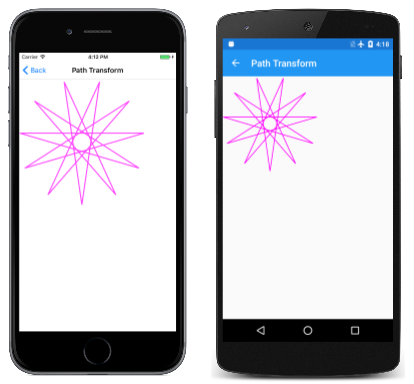
Suponha que você tenha um SKPath objeto que deseja exibir, mas prefere que ele tenha uma orientação um pouco diferente ou um ponto central diferente. Você pode modificar todas as coordenadas desse caminho chamando o Transform método de SKPath com um SKMatrix argumento. A página Transformação de Caminho demonstra como fazer isso. A PathTransform classe faz referência ao objeto em um campo, HendecagramPath mas usa seu construtor para aplicar uma transformação a esse caminho:
public class PathTransformPage : ContentPage
{
SKPath transformedPath = HendecagramArrayPage.HendecagramPath;
public PathTransformPage()
{
Title = "Path Transform";
SKCanvasView canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
SKMatrix matrix = SKMatrix.MakeScale(3, 3);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeRotationDegrees(360f / 22));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(300, 300));
transformedPath.Transform(matrix);
}
...
}
O HendecagramPath objeto tem um centro em (0, 0), e os 11 pontos da estrela se estendem para fora desse centro em 100 unidades em todas as direções. Isso significa que o caminho tem coordenadas positivas e negativas. A página Transformação de caminho prefere trabalhar com uma estrela três vezes maior e com todas as coordenadas positivas. Além disso, não quer que um ponto da estrela aponte para cima. Quer, em vez disso, que um ponto da estrela aponte para baixo. (Como o astro tem 11 pontos, não pode ter os dois.) Isso requer girar a estrela em 360 graus divididos por 22.
O construtor cria um SKMatrix objeto a partir de três transformações separadas usando o PostConcat método com o seguinte padrão, onde A, B e C são instâncias de SKMatrix:
SKMatrix matrix = A;
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, C);
Esta é uma série de multiplicações sucessivas, de modo que o resultado é o seguinte:
A × B × C
As multiplicações consecutivas ajudam a entender o que cada transformação faz. A transformação de escala aumenta o tamanho das coordenadas do caminho por um fator de 3, de modo que as coordenadas variam de –300 a 300. A transformada giratória gira a estrela em torno de sua origem. A transformação de tradução então a desloca em 300 pixels para a direita e para baixo, para que todas as coordenadas se tornem positivas.
Existem outras sequências que produzem a mesma matriz. Aqui está mais um:
SKMatrix matrix = SKMatrix.MakeRotationDegrees(360f / 22);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(100, 100));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(3, 3));
Isso gira o caminho em torno de seu centro primeiro e, em seguida, o traduz 100 pixels para a direita e para baixo para que todas as coordenadas sejam positivas. A estrela é então aumentada de tamanho em relação ao seu novo canto superior esquerdo, que é o ponto (0, 0).
O PaintSurface manipulador pode simplesmente renderizar este caminho:
public class PathTransformPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Magenta;
paint.StrokeWidth = 5;
canvas.DrawPath(transformedPath, paint);
}
}
}
Ele aparece no canto superior esquerdo da tela:
O construtor deste programa aplica a matriz ao caminho com a seguinte chamada:
transformedPath.Transform(matrix);
O caminho não retém essa matriz como uma propriedade. Em vez disso, ele aplica a transformação a todas as coordenadas do caminho. Se Transform for chamada novamente, a transformação será aplicada novamente, e a única maneira de voltar é aplicando outra matriz que desfaça a transformação. Felizmente, a SKMatrix estrutura define um TryInvert método que obtém a matriz que inverte uma dada matriz:
SKMatrix inverse;
bool success = matrix.TryInverse(out inverse);
O método é chamado TryInverse porque nem todas as matrizes são invertíveis, mas uma matriz não invertível provavelmente não será usada para uma transformação gráfica.
Você também pode aplicar uma transformação de matriz a um SKPoint valor, uma matriz de pontos, um SKRect, ou até mesmo apenas um único número dentro do seu programa. A SKMatrix estrutura suporta essas operações com uma coleção de métodos que começam com a palavra Map, como estes:
SKPoint transformedPoint = matrix.MapPoint(point);
SKPoint transformedPoint = matrix.MapPoint(x, y);
SKPoint[] transformedPoints = matrix.MapPoints(pointArray);
float transformedValue = matrix.MapRadius(floatValue);
SKRect transformedRect = matrix.MapRect(rect);
Se você usar esse último método, lembre-se de que a SKRect estrutura não é capaz de representar um retângulo rotacionado. O método só faz sentido para um SKMatrix valor que representa tradução e dimensionamento.
Experimentação Interativa
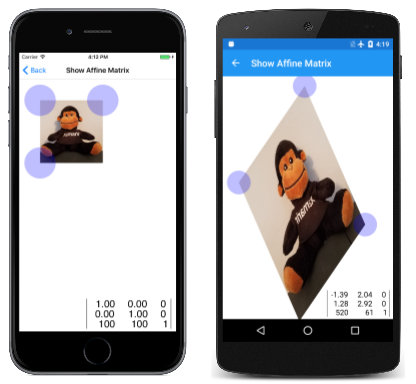
Uma maneira de ter uma ideia da transformação afim é movendo interativamente três cantos de um bitmap pela tela e vendo o que a transformação resulta. Esta é a ideia por trás da página Show Affine Matrix . Esta página requer duas outras classes que também são usadas em outras demonstrações:
A TouchPoint classe exibe um círculo translúcido que pode ser arrastado pela tela. TouchPoint requer que um SKCanvasView ou um elemento que é um pai de um SKCanvasView tenha o TouchEffect anexado. Defina a propriedade Capture como true. TouchAction No manipulador de eventos, o programa deve chamar o ProcessTouchEvent método em TouchPoint para cada TouchPoint instância. O método retorna true se o evento touch resultou na movimentação do ponto de toque. Além disso, o PaintSurface manipulador deve chamar o Paint método em cada TouchPoint instância, passando para ele o SKCanvas objeto.
TouchPoint demonstra uma maneira comum que um visual SkiaSharp pode ser encapsulado em uma classe separada. A classe pode definir propriedades para especificar características do visual, e um método nomeado Paint com um SKCanvas argumento pode renderizá-lo.
A Center propriedade de TouchPoint indica o local do objeto. Essa propriedade pode ser definida para inicializar o local; A propriedade é alterada quando o usuário arrasta o círculo ao redor da tela.
A página Mostrar matriz afim também requer a MatrixDisplay classe. Essa classe exibe as células de um SKMatrix objeto. Ele tem dois métodos públicos: Measure obter as dimensões da matriz renderizada e Paint exibi-la. A classe contém uma MatrixPaint propriedade de tipo SKPaint que pode ser substituída por um tamanho de fonte ou cor diferente.
O arquivo ShowAffineMatrixPage.xaml instancia o SKCanvasView e anexa um TouchEffectarquivo . O arquivo code-behind ShowAffineMatrixPage.xaml.cs cria três TouchPoint objetos e, em seguida, os define para posições correspondentes a três cantos de um bitmap que ele carrega de um recurso incorporado:
public partial class ShowAffineMatrixPage : ContentPage
{
SKMatrix matrix;
SKBitmap bitmap;
SKSize bitmapSize;
TouchPoint[] touchPoints = new TouchPoint[3];
MatrixDisplay matrixDisplay = new MatrixDisplay();
public ShowAffineMatrixPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
touchPoints[0] = new TouchPoint(100, 100); // upper-left corner
touchPoints[1] = new TouchPoint(bitmap.Width + 100, 100); // upper-right corner
touchPoints[2] = new TouchPoint(100, bitmap.Height + 100); // lower-left corner
bitmapSize = new SKSize(bitmap.Width, bitmap.Height);
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
}
...
}
Uma matriz afim é definida exclusivamente por três pontos. Os três TouchPoint objetos correspondem aos cantos superior esquerdo, superior direito e inferior esquerdo do bitmap. Como uma matriz afim só é capaz de transformar um retângulo em um paralelogramo, o quarto ponto é implícito pelos outros três. O construtor conclui com uma chamada para ComputeMatrix, que calcula as células de um SKMatrix objeto a partir desses três pontos.
O TouchAction manipulador chama o ProcessTouchEvent método de cada TouchPoint. O scale valor é convertido de Xamarin.Forms coordenadas em pixels:
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnTouchEffectAction(object sender, TouchActionEventArgs args)
{
bool touchPointMoved = false;
foreach (TouchPoint touchPoint in touchPoints)
{
float scale = canvasView.CanvasSize.Width / (float)canvasView.Width;
SKPoint point = new SKPoint(scale * (float)args.Location.X,
scale * (float)args.Location.Y);
touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
}
if (touchPointMoved)
{
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
canvasView.InvalidateSurface();
}
}
...
}
Se algum TouchPoint tiver sido movido, o método chamará ComputeMatrix novamente e invalidará a superfície.
O ComputeMatrix método determina a matriz implícita por esses três pontos. A matriz chamada A transforma um retângulo quadrado de um pixel em um paralelogramo com base nos três pontos, enquanto a transformação de escala chamada S escala o bitmap em um retângulo quadrado de um pixel. A matriz composta é S × A:
public partial class ShowAffineMatrixPage : ContentPage
{
...
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.Concat(ref result, A, S);
return result;
}
...
}
Finalmente, o PaintSurface método renderiza o bitmap com base nessa matriz, exibe a matriz na parte inferior da tela e renderiza os pontos de toque nos três cantos do bitmap:
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Display the bitmap using the matrix
canvas.Save();
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, 0, 0);
canvas.Restore();
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(matrix);
matrixDisplay.Paint(canvas, matrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Display the touchpoints
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
}
A tela do iOS abaixo mostra o bitmap quando a página é carregada pela primeira vez, enquanto as outras duas telas o mostram após alguma manipulação:
Embora pareça que os pontos de toque arrastam os cantos do bitmap, isso é apenas uma ilusão. A matriz calculada a partir dos pontos de toque transforma o bitmap para que os cantos coincidam com os pontos de toque.
É mais natural que os usuários movam, redimensionem e girem bitmaps não arrastando os cantos, mas usando um ou dois dedos diretamente no objeto para arrastar, apertar e girar. Isso é abordado no próximo artigo Manipulação de toque.
A razão da matriz 3 por 3
Seria de esperar que um sistema gráfico bidimensional exigisse apenas uma matriz de transformação 2 por 2:
│ ScaleX SkewY │
| x y | × │ │ = | x' y' |
│ SkewX ScaleY │
Isso funciona para escala, rotação e até inclinação, mas não é capaz da mais básica das transformações, que é a translação.
O problema é que a matriz 2 por 2 representa uma transformada linear em duas dimensões. Uma transformada linear preserva algumas operações aritméticas básicas, mas uma das implicações é que uma transformada linear nunca altera o ponto (0, 0). Uma transformação linear impossibilita a tradução.
Em três dimensões, uma matriz de transformação linear tem a seguinte aparência:
│ ScaleX SkewYX SkewZX │
| x y z | × │ SkewXY ScaleY SkewZY │ = | x' y' z' |
│ SkewXZ SkewYZ ScaleZ │
A célula rotulada significa que o valor distorce SkewXY a coordenada X com base em valores de Y, a célula SkewXZ significa que o valor distorce a coordenada X com base em valores de Z, e os valores distorcem de forma semelhante para as outras Skew células.
É possível restringir essa matriz de transformação 3D a um plano bidimensional definindo SkewZX e SkewZY a 0, e ScaleZ a 1:
│ ScaleX SkewYX 0 │
| x y z | × │ SkewXY ScaleY 0 │ = | x' y' z' |
│ SkewXZ SkewYZ 1 │
Se os gráficos bidimensionais são desenhados inteiramente no plano no espaço 3D onde Z é igual a 1, a multiplicação da transformada tem a seguinte aparência:
│ ScaleX SkewYX 0 │
| x y 1 | × │ SkewXY ScaleY 0 │ = | x' y' 1 |
│ SkewXZ SkewYZ 1 │
Tudo permanece no plano bidimensional onde Z é igual a 1, mas as SkewXZ células e SkewYZ efetivamente se tornam fatores de translação bidimensionais.
É assim que uma transformada linear tridimensional serve como uma transformada não-linear bidimensional. (Por analogia, as transformações em gráficos 3D são baseadas em uma matriz 4 por 4.)
A SKMatrix estrutura em SkiaSharp define propriedades para essa terceira linha:
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z` |
│ TransX TransY Persp2 │
Valores diferentes de zero de Persp0 e Persp1 resultam em transformações que movem objetos para fora do plano bidimensional onde Z é igual a 1. O que acontece quando esses objetos são movidos de volta para esse plano é abordado no artigo sobre Transformações Não-Afim.