Rotações 3D no SkiaSharp
Use transformações não afins para girar objetos 2D no espaço 3D.
Uma aplicação comum de transformações não-afins é simular a rotação de um objeto 2D no espaço 3D:
Esse trabalho envolve trabalhar com rotações tridimensionais e, em seguida, derivar uma transformada não afim SKMatrix que executa essas rotações 3D.
É difícil desenvolver essa SKMatrix transformação trabalhando apenas dentro de duas dimensões. O trabalho se torna muito mais fácil quando essa matriz 3 por 3 é derivada de uma matriz 4 por 4 usada em gráficos 3D. SkiaSharp inclui a SKMatrix44 classe para este propósito, mas algum fundo em gráficos 3D é necessário para entender as rotações 3D e a matriz de transformação 4 por 4.
Um sistema de coordenadas tridimensionais adiciona um terceiro eixo chamado Z. Conceitualmente, o eixo Z está em ângulo reto com a tela. Os pontos de coordenadas no espaço 3D são indicados com três números: (x, y, z). No sistema de coordenadas 3D usado neste artigo, valores crescentes de X estão à direita e valores crescentes de Y diminuem, assim como em duas dimensões. Valores Z positivos crescentes saem da tela. A origem é o canto superior esquerdo, assim como nos gráficos 2D. Você pode pensar na tela como um plano XY com o eixo Z em ângulos retos para este plano.
Isso é chamado de sistema de coordenadas à esquerda. Se você apontar o indicador para a mão esquerda na direção de coordenadas X positivas (para a direita), e seu dedo médio na direção de coordenadas Y crescentes (para baixo), então seu polegar aponta na direção de coordenadas Z crescentes — estendendo-se para fora da tela.
Em gráficos 3D, as transformações são baseadas em uma matriz 4 por 4. Aqui está a matriz de identidade 4 por 4:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 0 | | 0 0 0 1 |
Ao trabalhar com uma matriz 4 por 4, é conveniente identificar as células com seus números de linha e coluna:
| M11 M12 M13 M14 | | M21 M22 M23 M24 | | M31 M32 M33 M34 | | M41 M42 M43 M44 |
No entanto, a classe SkiaSharp Matrix44 é um pouco diferente. A única maneira de definir ou obter valores de células individuais é SKMatrix44 usando o Item indexador. Os índices de linha e coluna são baseados em zero em vez de baseados em um, e as linhas e colunas são trocadas. A célula M14 no diagrama acima é acessada usando o indexador [3, 0] em um SKMatrix44 objeto.
Em um sistema gráfico 3D, um ponto 3D (x, y, z) é convertido em uma matriz 1 por 4 para multiplicar pela matriz de transformação 4 por 4:
| M11 M12 M13 M14 |
| x y z 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Analogamente às transformações 2D que ocorrem em três dimensões, as transformações 3D são assumidas como ocorrendo em quatro dimensões. A quarta dimensão é referida como W, e o espaço 3D é assumido como existindo dentro do espaço 4D onde as coordenadas W são iguais a 1. As fórmulas de transformação são as seguintes:
x' = M11·x + M21·y + M31·z + M41
y' = M12·x + M22·y + M32·z + M42
z' = M13·x + M23·y + M33·z + M43
w' = M14·x + M24·y + M34·z + M44
É óbvio pelas fórmulas de transformação que as células M11, M22, M33 são fatores de escala nas direções X, Y e Z, e M41, e M43 são M42fatores de tradução nas direções X, Y e Z.
Para converter essas coordenadas de volta para o espaço 3D onde W é igual a 1, as coordenadas x', y' e z' são todas divididas por w':
x" = x' / w'
y" = y' / w'
z" = z' / w'
w" = w' / w' = 1
Essa divisão por w' fornece perspectiva no espaço 3D. Se w' é igual a 1, então nenhuma perspectiva ocorre.
As rotações no espaço 3D podem ser bastante complexas, mas as rotações mais simples são aquelas em torno dos eixos X, Y e Z. Uma rotação de ângulo α em torno do eixo X é esta matriz:
| 1 0 0 0 | | 0 cos(α) sin(α) 0 | | 0 –sin(α) cos(α) 0 | | 0 0 0 1 |
Os valores de X permanecem os mesmos quando submetidos a essa transformação. A rotação em torno do eixo Y deixa os valores de Y inalterados:
| cos(α) 0 –sin(α) 0 | | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 0 1 |
A rotação em torno do eixo Z é a mesma que em gráficos 2D:
| cos(α) sin(α) 0 0 | | –sin(α) cos(α) 0 0 | | 0 0 1 0 | | 0 0 0 1 |
A direção da rotação é implícita pela lateralidade do sistema de coordenadas. Este é um sistema canhoto, portanto, se você apontar o polegar da mão esquerda para valores crescentes para um determinado eixo — para a direita para rotação em torno do eixo X, para baixo para rotação em torno do eixo Y e em direção a você para rotação em torno do eixo Z — então a curva de seus outros dedos indica a direção da rotação para ângulos positivos.
SKMatrix44 tem métodos estáticos CreateRotation e CreateRotationDegrees generalizados que permitem especificar o eixo em torno do qual a rotação ocorre:
public static SKMatrix44 CreateRotationDegrees (Single x, Single y, Single z, Single degrees)
Para rotação em torno do eixo X, defina os três primeiros argumentos como 1, 0, 0. Para rotação em torno do eixo Y, defina-os como 0, 1, 0, e para rotação em torno do eixo Z, defina-os como 0, 0, 1.
A quarta coluna do 4 por 4 é para perspectiva. O SKMatrix44 não tem métodos para criar transformações de perspectiva, mas você mesmo pode criar um usando o seguinte código:
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
A razão para o nome depth do argumento será evidente em breve. Esse código cria a matriz:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 -1/depth | | 0 0 0 1 |
As fórmulas de transformação resultam no seguinte cálculo de w':
w' = –z / depth + 1
Isso serve para reduzir as coordenadas X e Y quando os valores de Z são menores que zero (conceitualmente atrás do plano XY) e para aumentar as coordenadas X e Y para valores positivos de Z. Quando a coordenada Z é depthigual a , então w' é zero, e as coordenadas se tornam infinitas. Sistemas gráficos tridimensionais são construídos em torno de uma metáfora da câmera, e o depth valor aqui representa a distância da câmera da origem do sistema de coordenadas. Se um objeto gráfico tem uma coordenada Z que é depth unidades da origem, ele está conceitualmente tocando a lente da câmera e se torna infinitamente grande.
Lembre-se de que você provavelmente usará esse perspectiveMatrix valor em combinação com matrizes de rotação. Se um objeto gráfico que está sendo girado tiver coordenadas X ou Y maiores que depth, a rotação desse objeto no espaço 3D provavelmente envolverá coordenadas Z maiores que depth. Isso deve ser evitado! Ao criar, perspectiveMatrix você deseja definir depth um valor suficientemente grande para todas as coordenadas no objeto gráfico, independentemente de como ele é girado. Isso garante que nunca haja divisão por zero.
Combinar rotações 3D e perspectiva requer multiplicar matrizes 4 por 4 juntas. Para isso, SKMatrix44 define métodos de concatenação. Se A e B forem SKMatrix44 objetos, o código a seguir define A igual a A × B:
A.PostConcat(B);
Quando uma matriz de transformação 4 por 4 é usada em um sistema gráfico 2D, ela é aplicada a objetos 2D. Esses objetos são planos e são assumidos como tendo coordenadas Z de zero. A multiplicação da transformada é um pouco mais simples do que a transformada mostrada anteriormente:
| M11 M12 M13 M14 |
| x y 0 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Esse valor 0 para z resulta em fórmulas de transformação que não envolvem nenhuma célula na terceira linha da matriz:
x' = M11·x + M21·y + M41
y' = M12·x + M22·y + M42
z' = M13·x + M23·y + M43
w' = M14·x + M24·y + M44
Além disso, a coordenada z' também é irrelevante aqui. Quando um objeto 3D é exibido em um sistema gráfico 2D, ele é recolhido para um objeto bidimensional ignorando os valores de coordenadas Z. As fórmulas de transformação são realmente apenas estas duas:
x" = x' / w'
y" = y' / w'
Isso significa que a terceira linha e a terceira coluna da matriz 4 por 4 podem ser ignoradas.
Mas se é assim, por que a matriz 4 por 4 é mesmo necessária em primeiro lugar?
Embora a terceira linha e a terceira coluna do 4 por 4 sejam irrelevantes para transformações bidimensionais, a terceira linha e a coluna desempenham um papel anterior a isso quando vários SKMatrix44 valores são multiplicados juntos. Por exemplo, suponha que você multiplique a rotação em torno do eixo Y com a transformação de perspectiva:
| cos(α) 0 –sin(α) 0 | | 1 0 0 0 | | cos(α) 0 –sin(α) sin(α)/depth | | 0 1 0 0 | × | 0 1 0 0 | = | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 1 -1/depth | | sin(α) 0 cos(α) -cos(α)/depth | | 0 0 0 1 | | 0 0 0 1 | | 0 0 0 1 |
No produto, a célula M14 agora contém um valor de perspectiva. Se você quiser aplicar essa matriz a objetos 2D, a terceira linha e coluna serão eliminadas para convertê-la em uma matriz 3 por 3:
| cos(α) 0 sin(α)/depth | | 0 1 0 | | 0 0 1 |
Agora ele pode ser usado para transformar um ponto 2D:
| cos(α) 0 sin(α)/depth |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
As fórmulas de transformação são:
x' = cos(α)·x
y' = y
z' = (sin(α)/depth)·x + 1
Agora divida tudo por z':
x" = cos(α)·x / ((sin(α)/depth)·x + 1)
y" = y / ((sin(α)/depth)·x + 1)
Quando os objetos 2D são girados com um ângulo positivo em torno do eixo Y, os valores X positivos recuam para o plano de fundo enquanto os valores X negativos vêm para o primeiro plano. Os valores X parecem se aproximar do eixo Y (que é governado pelo valor cosseno) à medida que as coordenadas mais distantes do eixo Y se tornam menores ou maiores à medida que se afastam do espectador ou se aproximam do espectador.
Ao usar SKMatrix44o , execute todas as operações de rotação e perspectiva 3D multiplicando vários SKMatrix44 valores. Em seguida, você pode extrair uma matriz bidimensional 3 por 3 da matriz 4 por 4 usando a MatrixSKMatrix44 propriedade da classe. Essa propriedade retorna um valor familiar SKMatrix .
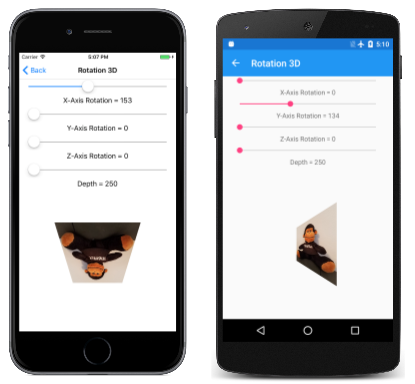
A página Rotação 3D permite que você experimente a rotação 3D. O arquivo Rotation3DPage.xaml instancia quatro controles deslizantes para definir a rotação em torno dos eixos X, Y e Z e definir um valor de profundidade:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.Rotation3DPage"
Title="Rotation 3D">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Margin" Value="20, 0" />
<Setter Property="Maximum" Value="360" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="xRotateSlider"
Grid.Row="0"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference xRotateSlider},
Path=Value,
StringFormat='X-Axis Rotation = {0:F0}'}"
Grid.Row="1" />
<Slider x:Name="yRotateSlider"
Grid.Row="2"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference yRotateSlider},
Path=Value,
StringFormat='Y-Axis Rotation = {0:F0}'}"
Grid.Row="3" />
<Slider x:Name="zRotateSlider"
Grid.Row="4"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference zRotateSlider},
Path=Value,
StringFormat='Z-Axis Rotation = {0:F0}'}"
Grid.Row="5" />
<Slider x:Name="depthSlider"
Grid.Row="6"
Maximum="2500"
Minimum="250"
ValueChanged="OnSliderValueChanged" />
<Label Grid.Row="7"
Text="{Binding Source={x:Reference depthSlider},
Path=Value,
StringFormat='Depth = {0:F0}'}" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="8"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Observe que o depthSlider é inicializado com um Minimum valor de 250. Isso implica que o objeto 2D que está sendo girado aqui tem coordenadas X e Y restritas a um círculo definido por um raio de 250 pixels em torno da origem. Qualquer rotação deste objeto no espaço 3D sempre resultará em valores de coordenadas inferiores a 250.
O arquivo code-behind Rotation3DPage.cs é carregado em um bitmap de 300 pixels quadrados:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
...
}
Se a transformação 3D estiver centrada nesse bitmap, as coordenadas X e Y variam entre –150 e 150, enquanto os cantos estão a 212 pixels do centro, portanto, tudo está dentro do raio de 250 pixels.
O PaintSurface manipulador cria SKMatrix44 objetos com base nos controles deslizantes e os multiplica juntos usando PostConcato . O SKMatrix valor extraído do objeto final SKMatrix44 é cercado por transformações de conversão para centralizar a rotação no centro da tela:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Use 3D matrix for 3D rotations and perspective
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, (float)xRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, (float)yRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, (float)zRotateSlider.Value));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / (float)depthSlider.Value;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the bitmap
canvas.SetMatrix(matrix);
float xBitmap = xCenter - bitmap.Width / 2;
float yBitmap = yCenter - bitmap.Height / 2;
canvas.DrawBitmap(bitmap, xBitmap, yBitmap);
}
}
Ao experimentar o quarto controle deslizante, você notará que as diferentes configurações de profundidade não afastam o objeto do visualizador, mas alteram a extensão do efeito de perspectiva:
O Animated Rotation 3D também usa SKMatrix44 para animar uma cadeia de texto no espaço 3D. O textPaint conjunto de objetos como um campo é usado no construtor para determinar os limites do texto:
public class AnimatedRotation3DPage : ContentPage
{
SKCanvasView canvasView;
float xRotationDegrees, yRotationDegrees, zRotationDegrees;
string text = "SkiaSharp";
SKPaint textPaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
TextSize = 100,
StrokeWidth = 3,
};
SKRect textBounds;
public AnimatedRotation3DPage()
{
Title = "Animated Rotation 3D";
canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
// Measure the text
textPaint.MeasureText(text, ref textBounds);
}
...
}
A OnAppearing substituição define três Xamarin.FormsAnimation objetos para animar os xRotationDegreescampos , yRotationDegreese zRotationDegrees em taxas diferentes. Observe que os períodos dessas animações são definidos como números primos (5 segundos, 7 segundos e 11 segundos) para que a combinação geral se repita apenas a cada 385 segundos, ou mais de 10 minutos:
public class AnimatedRotation3DPage : ContentPage
{
...
protected override void OnAppearing()
{
base.OnAppearing();
new Animation((value) => xRotationDegrees = 360 * (float)value).
Commit(this, "xRotationAnimation", length: 5000, repeat: () => true);
new Animation((value) => yRotationDegrees = 360 * (float)value).
Commit(this, "yRotationAnimation", length: 7000, repeat: () => true);
new Animation((value) =>
{
zRotationDegrees = 360 * (float)value;
canvasView.InvalidateSurface();
}).Commit(this, "zRotationAnimation", length: 11000, repeat: () => true);
}
protected override void OnDisappearing()
{
base.OnDisappearing();
this.AbortAnimation("xRotationAnimation");
this.AbortAnimation("yRotationAnimation");
this.AbortAnimation("zRotationAnimation");
}
...
}
Como no programa anterior, o PaintCanvas manipulador cria SKMatrix44 valores para rotação e perspectiva e os multiplica juntos:
public class AnimatedRotation3DPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Scale so text fits
float scale = Math.Min(info.Width / textBounds.Width,
info.Height / textBounds.Height);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(scale, scale));
// Calculate composite 3D transforms
float depth = 0.75f * scale * textBounds.Width;
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, xRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, yRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, zRotationDegrees));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the text
canvas.SetMatrix(matrix);
float xText = xCenter - textBounds.MidX;
float yText = yCenter - textBounds.MidY;
canvas.DrawText(text, xText, yText, textPaint);
}
}
Essa rotação 3D é cercada com várias transformações 2D para mover o centro de rotação para o centro da tela e dimensionar o tamanho da cadeia de texto para que ela tenha a mesma largura da tela: