Testar hipótese usando o t-Test

Artigo
05/06/2019

Importante

O suporte para o Machine Learning Studio (clássico) terminará em 31 de agosto de 2024. É recomendável fazer a transição para o Azure Machine Learning até essa data.

A partir de 1º de dezembro de 2021, você não poderá criar recursos do Machine Learning Studio (clássico). Até 31 de agosto de 2024, você pode continuar usando os recursos existentes do Machine Learning Studio (clássico).

Confira informações sobre como mover projetos de machine learning do ML Studio (clássico) para o Azure Machine Learning.
Saiba mais sobre o Azure Machine Learning.

A documentação do ML Studio (clássico) está sendo desativada e pode não ser atualizada no futuro.

Compara os meios de duas colunas usando um teste t

Categoria: Funções Estatísticas

Observação

Aplica-se a: somente Machine Learning Studio (clássico)

Módulos semelhantes do tipo "arrastar e soltar" estão disponíveis no designer do Azure Machine Learning.

Visão geral do módulo

Este artigo descreve como usar a hipótese de teste usando o módulo t-Test no Machine Learning Studio (clássico), para gerar pontuações para três tipos de testes t:

Teste t único de exemplo
Teste t emparelhado
Teste t não emparelhado

Em geral, um teste de t ajuda a comparar se dois grupos têm médias diferentes. Por exemplo, suponha que você esteja avaliando dados de testes para pacientes que receberam a Droga A versus pacientes que receberam a Droga B e precisa comparar uma métrica de taxa de recuperação de ambos os grupos. A hipótese nula presume que a taxa de recuperação é a mesma nos dois grupos e, além disso, que os valores da taxa de recuperação têm uma distribuição normal em ambos os grupos.

Usando a Hipótese de Teste usando t-Test e fornecendo as colunas que contêm as taxas de recuperação como entrada, você pode obter pontuações que indicam se a diferença é significativa, o que significaria que a hipótese nula deve ser rejeitada. O teste levará em consideração fatores como quão grande é a diferença entre os valores, o tamanho da amostra (maior é melhor) e o tamanho do desvio padrão (menor é melhor).

Examinando os resultados da hipótese de teste usando o módulo t-Test , você pode determinar se a hipótese nula é TRUE ou FALSE e examinar as pontuações de confiança (P) do teste t.

Como escolher um teste t

Escolha um único exemplo de teste t quando essas condições se aplicarem:

Você tem um único exemplo de pontuações.
Todas as pontuações são independentes umas das outras.
A distribuição de amostragem de xˉ é normal.

Em geral, o teste de t de exemplo único é usado para comparar um valor médio para um número conhecido.

Escolha um teste t emparelhado quando essas condições se aplicarem:

Você tem pares de resultados correspondentes. Por exemplo, você pode ter duas medidas diferentes por pessoa ou pares de indivíduos correspondentes (como um marido e mulher).
Cada par de pontuações é independente de todos os outros pares.
A distribuição de amostragem de d é normal.

Um teste de t é útil ao comparar os casos relacionados. Criando as diferenças entre as pontuações de casos emparelhados, você pode determinar se a diferença total é estatisticamente significativa.

Escolha um t-test não pago quando essas condições se aplicarem:

Você tem duas amostras independentes de pontuações. Ou seja, não há nenhuma base para pontuações de emparelhamento no exemplo 1 com aqueles no exemplo 2.
Todas as pontuações dentro de uma amostra são independentes de todas as outras pontuações dentro desse exemplo.
A distribuição de amostragem de x1-x2 é normal.
Opcionalmente, satisfaça o requisito para que a variação entre os grupos seja aproximadamente igual.

Como configurar a hipótese de teste usando t-test

Use um único conjunto de dados como entrada. As colunas que você está comparando devem estar no mesmo conjunto de dados.

Se você precisar comparar colunas de conjuntos de dados diferentes, poderá isolar cada coluna para comparar usando Selecionar Colunas no Conjunto de Dados e, em seguida, mesclar em um conjunto de dados usando Adicionar Colunas.

Adicione a hipótese de teste usando o módulo t-Test ao experimento.

Você pode encontrar este módulo na categoria Funções Estatísticas no Studio (clássico).
Adicione o conjunto de dados que contém a coluna ou colunas que você deseja analisar.
Decida qual tipo de teste t é apropriado para seus dados. Veja como escolher um teste t.
Exemplo único: se você estiver usando um único exemplo, defina estes parâmetros:
- Μ com hipóteses nulas: digite o valor a ser usado como a média com hipóteses nulas para a amostra. Isso especifica o valor médio esperado em relação ao qual a média de exemplo será testada.
- Coluna de destino: use o Seletor de Colunas para escolher uma única coluna numérica para teste.
- Tipo de hipótese: escolha um teste de uma ou duas caudas. O padrão é um teste bicaudal. Esse é o tipo mais comum de teste, em que a distribuição esperada é simétrica em torno de zero.
  
  A opção One Tail GT é para um final maior que o teste. Esse teste dá mais poder para detectar um efeito em uma direção, não testando o efeito na outra direção.
  
  A opção One Tail LT fornece um teste com uma cauda a menos do que o teste.
- α: especifique um fator de confiança. Esse valor é usado para avaliar o valor de P (a primeira saída do módulo). Se p for menor que o fator de confiança, a hipótese nula será rejeitada.
PairedSamples: se você estiver comparando dois exemplos da mesma população, defina estes parâmetros:
- Μ com hipóteses nulas: digite um valor que representa a diferença de exemplo entre o par de amostras.
- Coluna de destino: use o Seletor de Coluna para escolher as duas colunas numéricas a serem testadas.
- Tipo de hipótese: selecione um teste de uma ou duas caudas. O padrão é um teste bicaudal.
- α: especifique o fator de confiança. Esse valor é usado para avaliar o valor de P (a primeira saída do módulo)> Se p for menor que o fator de confiança, a hipótese nula será rejeitada.
UnpairedSamples: se você comparar duas amostras não pagas, defina estes parâmetros:
- Suponha a mesma variação: desmarque essa opção quando os exemplos forem de populações diferentes.
- μ1 com hipóteses nulas: digite a média para a primeira coluna.
- μ2 com hipóteses nulas: digite a média para a segunda coluna.
- Colunas de destino: use o Seletor de Colunas para escolher duas colunas numéricas para testar.
- Tipo de hipótese: indique se o teste é de uma ou duas caudas. O padrão é um teste bicaudal.
- α: especifique o fator de confiança. Esse valor é usado para avaliar o valor de P (a primeira saída do módulo)> Se p for menor que o fator de confiança, a hipótese nula será rejeitada.
Execute o experimento.

Resultados

A saída do módulo é um conjunto de dados que contém as pontuações de teste t e uma transformação que você pode salvar opcionalmente para aplicar novamente a esse ou outro conjunto de dados usando a Transformação Aplicar.

O conjunto de dados de pontuações contém esses valores, independentemente do tipo de teste t usado:

Uma pontuação de probabilidade que indica a confiança da hipótese nula
Um valor que indica se a hipótese Nula deve ser rejeitada

Dica

Lembre-se de que o objetivo é determinar se você pode rejeitar a hipótese nula. Uma pontuação 0 não significa que você deve aceitar a hipótese nula: significa que você não tem dados suficientes e precisa de uma investigação mais aprofundada.

Observações técnicas

O módulo nomeia automaticamente as colunas de saída de acordo com as convenções a seguir, dependendo do tipo de teste t selecionado e se o resultado rejeitou ou aceitou a hipótese nula.

Dadas as colunas de entrada com nomes {0} e {1}o módulo cria os seguintes nomes:

Colunas	SingleSampleSet	PairedSamples	UnpairedSamples
Coluna de saída P	P_ss({0})	P_ps({0}, {1})	P_us({0}, {1})
Coluna de saída RejectH0	RejectH0_ss({0})"	RejectH0_ps({0}, {1})	RejectH0_us({0}, {1})

Como as pontuações são computadas

Este módulo calcula e usa o desvio padrão de exemplo; portanto, a equação é usada (n-1) no denominador.

Pontuações de computação para um teste de exemplo único

Tendo em conta um único exemplo de pontuações, todas independentes entre si, e uma distribuição normal, a pontuação é calculada da seguinte maneira:

Imagine a seguinte entrada:
- Uma única coluna de valores do conjunto de dados
- A hipótese nula (H0) parâmetro μ0
- A pontuação de confiança especificada por α
Extraia o número de amostras (n).
Calcule a média dos dados de exemplo.
Calcule o desvio padrão dos dados de exemplo.
Calcular t e graus de liberdade (df):
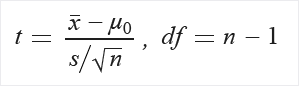
Extraia a probabilidade P da tabela de distribuição T usando t e df.

Pontuações de computação para um teste t emparelhado

Tendo em conta um conjunto correspondente de pontuações, com cada par independente do outro, e uma distribuição normal em cada conjunto, a pontuação é calculada da seguinte maneira:

Imagine a seguinte entrada:
- Duas colunas de valores do conjunto de dados
- O parâmetro de hipótese nula (H0) d0
- A pontuação de confiança especificada por α
Extraia algum número de pares de exemplo (n).
Calcule a média das diferenças para os dados de exemplo:
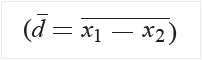
Calcule o desvio padrão de diferenças (sd).
Calcular t e os graus de liberdade (df):
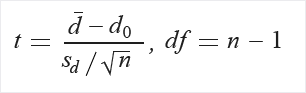
Extraia probabilidade (P) da tabela de distribuição (T) usando t e df.

Pontuações de computação para um t-test não remunerado

Tendo em conta dois exemplos independentes de pontuações, com uma distribuição normal de valores em cada exemplo, a pontuação é calculada da seguinte maneira:

Imagine a seguinte entrada:
- Um conjunto de dados que contém duas colunas de doubles
- O parâmetro de hipótese nula (H0) (d0)
- A pontuação de confiança especificada por α
Extraia um número de amostras em cada grupo, n1 e n2.
Calcule as médias para cada um dos conjuntos de exemplo.
Calcule o desvio padrão para cada grupo como s1 e s2.
Calcular t e graus de liberdade (df):

Opcionalmente, satisfaça o requisito para que a variação entre os grupos seja aproximadamente igual, como a seguir:

Calcule o desvio padrão em pool primeiro:
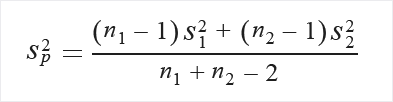
Se não houver nenhuma suposição sobre a igualdade de variação, calcule da seguinte forma:
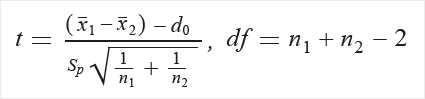
Extraia P da tabela de distribuição (T) usando t e df.

Computando a hipótese nula

A probabilidade da hipótese nula, designada como P, é calculada da seguinte maneira:

Se P < α, defina o sinalizador Reject como True.
Se P ≥ α, defina o sinalizador Reject como False.

Entradas esperadas

Nome	Tipo	Descrição
Dataset	Tabela de Dados	Conjunto de dados de entrada

Parâmetros do módulo

Nome	Intervalo	Type	Padrão	Descrição
Tipo de hipótese	Qualquer	Hipótese	Bicaudal	Tipo de hipótese nula de teste t do Student
Μ com hipóteses nulas	Qualquer	Float	0,0	Para o teste t de exemplo único, a média hipotética nula do exemplo Para o teste t emparelhado, a diferença do exemplo
Coluna(s) de destino	Qualquer	ColumnSelection	Nenhum	Padrão de seleção de coluna (s) de destino
Suponha variâncias iguais	Qualquer	Booliano	verdadeiro	Suponha que as variações dos dois exemplos sejam iguais Se aplica apenas a exemplos não emparelhados
μ1 com hipóteses nulas	Qualquer	Float	0,0	Média hipotética NULL para o primeiro exemplo
Α	[0,0;1,0]	Float	0,95	Fator de confiança (se P é menor do que o fator de confiança, a hipótese nula é rejeitada)

Saídas

Nome	Tipo	Descrição
P	Tabela de Dados	Uma pontuação de probabilidade que indica a confiança da hipótese nula
Rejeitar H0	Tabela de Dados	Valor que indica se a hipótese Nula deve ser rejeitada

Exceções

Exceção	Descrição
Erro 0003	Ocorrerá uma exceção se uma ou mais das entradas for nula ou estiver vazia.
Erro 0008	Ocorrerá uma exceção se o parâmetro não estiver no intervalo.
Erro 0017	Ocorre uma exceção se uma ou mais colunas especificadas tem um tipo que não é suportado pelo módulo atual.
Erro 0020	Ocorre uma exceção se o número de colunas em alguns dos conjuntos de dados transmitidos para o módulo for muito pequeno.
Erro 0021	Ocorre uma exceção se o número de linhas em alguns dos conjuntos de dados passados para o módulo for muito pequeno.
Erro 0031	Ocorre uma exceção se o número de colunas no conjunto de colunas é menor do que o necessário.
Erro 0032	Ocorre uma exceção se o argumento não é um número.
Erro 0033	Ocorre uma exceção se o argumento é infinito.

Para obter uma lista de erros específicos dos módulos do Studio (clássico), consulte Machine Learning códigos de erro.

Para obter uma lista de exceções de API, consulte Machine Learning códigos de erro da API REST.

Confira também

Funções estatísticas

Compartilhar via