Przekształcenia nieafiniczne
Tworzenie efektów perspektywy i naciśnięcia z trzecią kolumną macierzy przekształcania
Translacja, skalowanie, rotacja i niesymetryczność są klasyfikowane jako przekształcenia affine . Przekształcenia affiny zachowują linie równoległe. Jeśli dwa wiersze są równoległe przed przekształceniem, pozostają one równoległe po przekształceniu. Prostokąty są zawsze przekształcane na równoległe.
Jednak SkiaSharp jest również w stanie przekształcić nie-affine, które mają możliwość przekształcenia prostokąta w każdy wypukły czworokąt:

Czworokąt wypukły jest czterostronną postacią z kątami wewnętrznymi zawsze mniejszymi niż 180 stopni i bokami, które nie przecinają się nawzajem.
Wynik przekształcenia nieaffine powoduje, gdy trzeci wiersz macierzy przekształcania jest ustawiony na wartości inne niż 0, 0 i 1. SKMatrix Pełne mnożenie to:
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z' |
│ TransX TransY Persp2 │
Wynikowe formuły przekształcania to:
x' = ScaleX·x + SkewX·y + TransX
y' = SkewY·x + ScaleY·y + TransY
z' = Persp0·x + Persp1·y + Persp2
Podstawową regułą używania macierzy 3-do-3 dla przekształceń dwuwymiarowych jest to, że wszystko pozostaje na płaszczyźnie, gdzie Z równa się 1. O ile Persp0 wartość i Persp1 nie ma wartości 0, a Persp2 równa 1, przekształcenie przeniosło współrzędne Z z tej płaszczyzny.
Aby przywrócić ten element do transformacji dwuwymiarowej, współrzędne muszą zostać przeniesione z powrotem do tej płaszczyzny. Wymagany jest kolejny krok. Wartości x', y i z muszą być podzielone przez z':
x" = x' / z'
y" = y' / z'
z" = z' / z' = 1
Są one znane jako homogeniczne współrzędne i zostały opracowane przez matematyka AugustA Ferdynanda Möbiusa, znacznie lepiej znane ze swojej topologicznej dziwności, Pas Möbius.
Jeśli wartość z wynosi 0, dzielenie powoduje nieskończone współrzędne. W rzeczywistości jedną z motywacji Möbiusa do opracowania homogenicznych współrzędnych była zdolność do reprezentowania nieskończonych wartości ze skończonymi liczbami.
Podczas wyświetlania grafiki należy jednak unikać renderowania elementów ze współrzędnymi, które przekształcają się w nieskończone wartości. Te współrzędne nie zostaną renderowane. Wszystko w pobliżu tych współrzędnych będzie bardzo duże i prawdopodobnie nie wizualnie spójne.
W tym równaniu nie chcesz, aby wartość z stała się równaniem zero:
z' = Persp0·x + Persp1·y + Persp2
W związku z tym te wartości mają pewne praktyczne ograniczenia:
Persp2 Komórka może mieć wartość zero lub nie zero. Jeśli Persp2 wartość to zero, to z' jest zero dla punktu (0, 0) i to zwykle nie jest pożądane, ponieważ ten punkt jest bardzo powszechny w dwuwymiarowej grafice. Jeśli Persp2 wartość nie jest równa zero, wówczas nie ma utraty ogólnej wartości, jeśli Persp2 jest ustalona na 1. Jeśli na przykład określisz, że Persp2 wartość powinna wynosić 5, możesz po prostu podzielić wszystkie komórki w macierzy przez 5, co oznacza Persp2 , że równa się 1, a wynik będzie taki sam.
Z tych powodów Persp2 często jest stała na 1, co jest tą samą wartością w macierzy tożsamości.
Ogólnie rzecz biorąc, Persp0 i Persp1 są małymi liczbami. Załóżmy na przykład, że zaczynasz od macierzy tożsamości, ale ustawiono wartość Persp0 0,01:
| 1 0 0.01 | | 0 1 0 | | 0 0 1 |
Formuły przekształcania to:
x' = x / (0,01·x + 1)
y' = y / (0,01·x + 1)
Teraz użyj tej transformacji, aby renderować pole kwadratowe o rozmiarze 100 pikseli rozmieszczone na początku. Oto jak przekształcane są cztery rogi:
(0, 0) → (0, 0)
(0, 100) → (0, 100)
(100, 0) → (50, 0)
(100, 100) → (50, 50)
Gdy x ma wartość 100, mianownik z wynosi 2, więc współrzędne x i y są skutecznie o połowę mniejsze. Prawa strona pola staje się krótsza niż lewa strona:
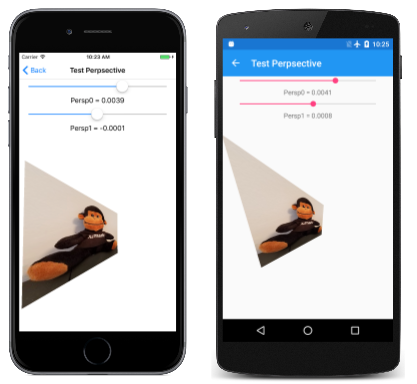
Część Persp tych nazw komórek odnosi się do "perspektywy", ponieważ foreshortening sugeruje, że pole jest teraz przechylone z prawej strony dalej od przeglądarki.
Strona Test perspective (Perspektywa testu) umożliwia eksperymentowanie z wartościami Persp0 i Pers1 uzyskanie doświadczenia w sposobie ich działania. Rozsądne wartości tych komórek macierzy są tak małe, że Slider w platforma uniwersalna systemu Windows nie mogą one prawidłowo obsłużyć. Aby uwzględnić problem platformy UWP, dwa Slider elementy w pliku TestPerspective.xaml muszą zostać zainicjowane do zakresu od –1 do 1:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.TestPerspectivePage"
Title="Test Perpsective">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Minimum" Value="-1" />
<Setter Property="Maximum" Value="1" />
<Setter Property="Margin" Value="20, 0" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="persp0Slider"
Grid.Row="0"
ValueChanged="OnPersp0SliderValueChanged" />
<Label x:Name="persp0Label"
Text="Persp0 = 0.0000"
Grid.Row="1" />
<Slider x:Name="persp1Slider"
Grid.Row="2"
ValueChanged="OnPersp1SliderValueChanged" />
<Label x:Name="persp1Label"
Text="Persp1 = 0.0000"
Grid.Row="3" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="4"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Programy obsługi zdarzeń dla suwaków w TestPerspectivePage pliku za kodem dzielą wartości przez 100, aby mieściły się w zakresie od –0,01 do 0,01. Ponadto konstruktor ładuje się w mapie bitowej:
public partial class TestPerspectivePage : ContentPage
{
SKBitmap bitmap;
public TestPerspectivePage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnPersp0SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp0Label.Text = String.Format("Persp0 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
void OnPersp1SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp1Label.Text = String.Format("Persp1 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
...
}
Procedura PaintSurface obsługi oblicza SKMatrix wartość o nazwie perspectiveMatrix na podstawie wartości tych dwóch suwaków podzielonych przez 100. Jest to połączone z dwoma przekształceniami, które umieszczają środek tej transformacji w środku mapy bitowej:
public partial class TestPerspectivePage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Calculate perspective matrix
SKMatrix perspectiveMatrix = SKMatrix.MakeIdentity();
perspectiveMatrix.Persp0 = (float)persp0Slider.Value / 100;
perspectiveMatrix.Persp1 = (float)persp1Slider.Value / 100;
// Center of screen
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
SKMatrix.PostConcat(ref matrix, perspectiveMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(xCenter, yCenter));
// Coordinates to center bitmap on canvas
float x = xCenter - bitmap.Width / 2;
float y = yCenter - bitmap.Height / 2;
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
}
Oto kilka przykładowych obrazów:
Podczas eksperymentowania z suwakami przekonasz się, że wartości przekraczające 0,0066 lub poniżej –0,0066 powodują, że obraz nagle staje się złamany i niespójny. Przekształcana mapa bitowa to 300 pikseli kwadratowych. Jest przekształcany w stosunku do środka, więc współrzędne zakresu mapy bitowej od –150 do 150. Przypomnij sobie, że wartość z to:
z' = Persp0·x + Persp1·y + 1
Jeśli Persp0 wartość lub Persp1 jest większa niż 0,0066 lub mniejsza niż –0,0066, zawsze istnieje pewna współrzędna mapy bitowej, która powoduje wartość z zero. Powoduje to podział o zero, a renderowanie staje się bałaganem. W przypadku używania przekształceń innych niż affine należy unikać renderowania niczego ze współrzędnymi, które powodują dzielenie o zero.
Ogólnie rzecz biorąc, nie będziesz ustawiać Persp0 i Persp1 w izolacji. Często konieczne jest również ustawienie innych komórek w macierzy w celu osiągnięcia niektórych typów transformacji nieafinowych.
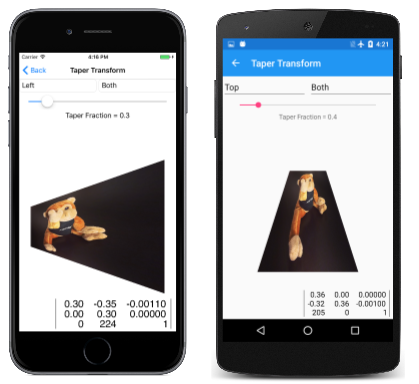
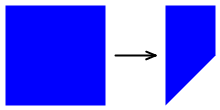
Jedną z takich transformacji innych niż affine jest taper transform. Ten typ transformacji innej niż affine zachowuje ogólne wymiary prostokąta, ale tapers po jednej stronie:
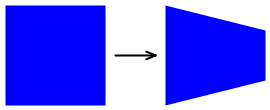
Klasa TaperTransform wykonuje uogólnione obliczenie przekształcenia nieaffine na podstawie następujących parametrów:
- prostokątny rozmiar przekształcanego obrazu,
- wyliczenie wskazujące bok prostokąta, który dotyka,
- inną wyliczenie, która wskazuje, jak się naciśnięć, i
- zakres taśmowania.
Oto kod:
enum TaperSide { Left, Top, Right, Bottom }
enum TaperCorner { LeftOrTop, RightOrBottom, Both }
static class TaperTransform
{
public static SKMatrix Make(SKSize size, TaperSide taperSide, TaperCorner taperCorner, float taperFraction)
{
SKMatrix matrix = SKMatrix.MakeIdentity();
switch (taperSide)
{
case TaperSide.Left:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp0 = (taperFraction - 1) / size.Width;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Top:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp1 = (taperFraction - 1) / size.Height;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Right:
matrix.ScaleX = 1 / taperFraction;
matrix.Persp0 = (1 - taperFraction) / (size.Width * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
break;
}
break;
case TaperSide.Bottom:
matrix.ScaleY = 1 / taperFraction;
matrix.Persp1 = (1 - taperFraction) / (size.Height * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
break;
}
break;
}
return matrix;
}
}
Ta klasa jest używana na stronie Taper Transform (Przekształcanie taper). Plik XAML tworzy wystąpienie dwóch Picker elementów, aby wybrać wartości wyliczenia i element Slider do wybrania ułamka taper. Procedura PaintSurface obsługi łączy transformację taper z dwoma przekształceniami translacji, aby przekształcić w stosunku do lewego górnego rogu mapy bitowej:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
TaperSide taperSide = (TaperSide)taperSidePicker.SelectedItem;
TaperCorner taperCorner = (TaperCorner)taperCornerPicker.SelectedItem;
float taperFraction = (float)taperFractionSlider.Value;
SKMatrix taperMatrix =
TaperTransform.Make(new SKSize(bitmap.Width, bitmap.Height),
taperSide, taperCorner, taperFraction);
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(taperMatrix);
matrixDisplay.Paint(canvas, taperMatrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Center bitmap on canvas
float x = (info.Width - bitmap.Width) / 2;
float y = (info.Height - bitmap.Height) / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-x, -y);
SKMatrix.PostConcat(ref matrix, taperMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(x, y));
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
Oto kilka przykładów:
Innym typem uogólnionych przekształceń innych niż affine jest rotacja 3D, która jest pokazana w następnym artykule, rotacje 3D.
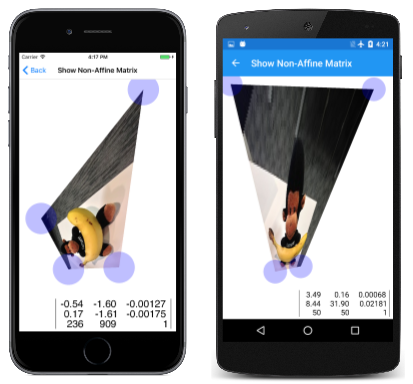
Transformacja nieaffina może przekształcić prostokąt w każdy wypukły czworokąt. Jest to pokazane na stronie Show Non-Affine Matrix (Pokaż macierz nienależącą do Affine). Jest on bardzo podobny do strony Show Affine Matrix (Pokaż macierz) z artykułu Matrix Transforms (Przekształcenia macierzy), z tą różnicą, że ma czwarty TouchPoint obiekt do manipulowania czwartym róg mapy bitowej:
Tak długo, jak nie próbujesz zrobić wewnętrznego kąta jednego z narożników mapy bitowej większej niż 180 stopni lub zrobić dwa boki przecinają się ze sobą, program pomyślnie oblicza przekształcenie przy użyciu tej metody z ShowNonAffineMatrixPage klasy:
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL, SKPoint ptLR)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
// Non-Affine transform
SKMatrix inverseA;
A.TryInvert(out inverseA);
SKPoint abPoint = inverseA.MapPoint(ptLR);
float a = abPoint.X;
float b = abPoint.Y;
float scaleX = a / (a + b - 1);
float scaleY = b / (a + b - 1);
SKMatrix N = new SKMatrix
{
ScaleX = scaleX,
ScaleY = scaleY,
Persp0 = scaleX - 1,
Persp1 = scaleY - 1,
Persp2 = 1
};
// Multiply S * N * A
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.PostConcat(ref result, S);
SKMatrix.PostConcat(ref result, N);
SKMatrix.PostConcat(ref result, A);
return result;
}
Aby ułatwić obliczanie, ta metoda uzyskuje całkowitą transformację jako produkt trzech oddzielnych przekształceń, które są symbolizowane tutaj ze strzałkami pokazującymi, jak te przekształcenia modyfikują cztery rogi mapy bitowej:
(0, 0) → (0, 0) → (0, 0) → (x0, y0) (w lewym górnym rogu)
(0, H) → (0, 1) → (0, 1) → (x1, y1) (w lewym dolnym rogu)
(W, 0) → (1, 0) → (1, 0) → (x2, y2) (w prawym górnym rogu)
(W, H) → (1, 1) → (a, b) → (x3, y3) (w prawym dolnym rogu)
Końcowe współrzędne po prawej stronie to cztery punkty skojarzone z czterema punktami dotykowymi. Są to końcowe współrzędne narożników mapy bitowej.
W i H reprezentują szerokość i wysokość mapy bitowej. Pierwsza transformacja S po prostu skaluje mapę bitową do kwadratu o rozmiarze 1 pikseli. Druga transformacja to transformacja Nnieaffine, a trzecia to transformacja Aaffine . Ta transformacja affine opiera się na trzech punktach, więc jest tak samo jak wcześniejsza metoda affine ComputeMatrix i nie obejmuje czwartego wiersza z punktem (a, b).
Wartości a i b są obliczane tak, aby trzecia transformacja została affine. Kod uzyskuje odwrotność przekształcenia affine, a następnie używa go do mapowania prawego dolnego rogu. To jest punkt (a, b).
Innym zastosowaniem przekształceń innych niż affine jest naśladowanie trójwymiarowej grafiki. W następnym artykule zobaczysz, jak obracać dwuwymiarową grafikę w przestrzeni 3D.