Przekształcenia macierzy w skiaSharp

Dowiedz się więcej na temat przekształceń SkiaSharp za pomocą uniwersalnej macierzy transformacji

Wszystkie przekształcenia zastosowane do SKCanvas obiektu są konsolidowane w jednym wystąpieniu SKMatrix struktury. Jest to standardowa macierz transformacji 3-by-3 podobna do tych we wszystkich nowoczesnych systemach graficznych 2D.

Jak już wiesz, można użyć przekształceń w SkiaSharp bez znajomości macierzy transformacji, ale macierz transformacji jest ważna z perspektywy teoretycznej i ma kluczowe znaczenie w przypadku używania przekształceń do modyfikowania ścieżek lub obsługi złożonych danych wejściowych dotykowych, z których oba przedstawiono w tym artykule i następnego.

Bieżąca macierz przekształcania zastosowana do obiektu SKCanvas jest dostępna w dowolnym momencie przez uzyskanie dostępu do właściwości tylko TotalMatrix do odczytu. Możesz ustawić nową macierz przekształcania przy użyciu SetMatrix metody i przywrócić tę macierz przekształcania do wartości domyślnych, wywołując metodę ResetMatrix.

Jedynym innym SKCanvas elementem członkowskim, który bezpośrednio współpracuje z przekształceniem macierzy kanwy, jest Concat łączenie dwóch macierzy przez pomnożenie ich razem.

Domyślna macierz przekształcania to macierz tożsamości i składa się z 1 w komórkach ukośnych i 0 gdzie indziej:

| 1  0  0 |
| 0  1  0 |
| 0  0  1 |

Macierz tożsamości można utworzyć przy użyciu metody statycznej SKMatrix.MakeIdentity :

SKMatrix matrix = SKMatrix.MakeIdentity();

Domyślny SKMatrix konstruktor nie zwraca macierzy tożsamości. Zwraca macierz ze wszystkimi komórkami ustawionymi na zero. Nie używaj konstruktora SKMatrix , chyba że planujesz ręcznie ustawić te komórki.

Gdy skiaSharp renderuje obiekt graficzny, każdy punkt (x, y) jest skutecznie konwertowany na macierz 1-by-3 z wartością 1 w trzeciej kolumnie:

| x  y  1 |

Ta macierz 1-by-3 reprezentuje trójwymiarowy punkt ze współrzędną Z ustawioną na 1. Istnieją matematyczne przyczyny (omówione w dalszej części), dlaczego transformacja macierzy dwuwymiarowej wymaga pracy w trzech wymiarach. Można traktować tę macierz 1-by-3 jako reprezentującą punkt w układzie współrzędnych 3D, ale zawsze na płaszczyźnie 2D, gdzie Z równa się 1.

Ta macierz 1-by-3 jest następnie mnożona przez macierz przekształcania, a wynik jest punktem renderowanym na kanwie:

              | 1  0  0 |
| x  y  1 | × | 0  1  0 | = | x'  y'  z' |
              | 0  0  1 |

Korzystając ze standardowego mnożenia macierzy, przekonwertowane punkty są następujące:

x' = x

y' = y

z' = 1

Jest to domyślna transformacja.

Translate Gdy metoda jest wywoływana w SKCanvas obiekcie, tx argumenty i ty do metody stają się pierwszymi dwoma komórkami Translate w trzecim wierszu macierzy przekształcania:

|  1   0   0 |
|  0   1   0 |
| tx  ty   1 |

Mnożenie jest teraz następujące:

              |  1   0   0 |
| x  y  1 | × |  0   1   0 | = | x'  y'  z' |
              | tx  ty   1 |

Oto formuły przekształcania:

x' = x + tx

y' = y + ty

Czynniki skalowania mają wartość domyślną 1. Podczas wywoływania Scale metody na nowym SKCanvas obiekcie wynikowa macierz przekształcania zawiera sx argumenty i sy w komórkach ukośnych:

              | sx   0   0 |
| x  y  1 | × |  0  sy   0 | = | x'  y'  z' |
              |  0   0   1 |

Formuły przekształcania są następujące:

x' = sx · x

y' = sy · y

Macierz przekształcania po wywołaniu Skew zawiera dwa argumenty w komórkach macierzy sąsiadujących z czynnikami skalowania:

              │   1   ySkew   0 │
| x  y  1 | × │ xSkew   1     0 │ = | x'  y'  z' |
              │   0     0     1 │

Formuły przekształcania to:

x' = x + xSkew · y

y' = ySkew · x + y

W przypadku wywołania metody RotateDegrees lub RotateRadians kąta α macierz przekształcania wygląda następująco:

              │  cos(α)  sin(α)  0 │
| x  y  1 | × │ –sin(α)  cos(α)  0 │ = | x'  y'  z' |
              │    0       0     1 │

Oto formuły przekształcania:

x' = cos(α) · x - sin(α) · y

y' = sin(α) · x - cos(α) · y

Gdy α wynosi 0 stopni, jest to macierz tożsamości. Gdy α wynosi 180 stopni, macierz przekształcania jest następująca:

| –1   0   0 |
|  0  –1   0 |
|  0   0   1 |

Rotacja 180 stopni jest równoważna przerzucaniu obiektu w poziomie i w pionie, co jest również realizowane przez ustawienie czynników skalowania –1.

Wszystkie te typy przekształceń są klasyfikowane jako przekształcenia affine . Przekształcenia Affine nigdy nie obejmują trzeciej kolumny macierzy, która pozostaje w wartościach domyślnych 0, 0 i 1. W artykule Nie-Affine Transforms omówiono przekształcenia inne niż affine.

mnożenie macierzy

Jedną z znaczących zalet korzystania z macierzy przekształcania jest to, że przekształcenia złożone mogą być uzyskiwane przez mnożenie macierzy, które jest często określane w dokumentacji SkiaSharp jako łączenie. Wiele metod związanych z transformacją odnosi SKCanvas się do "wstępnego łączenia" lub "wstępnego łączenia". Odnosi się to do kolejności mnożenia, co jest ważne, ponieważ mnożenie macierzy nie jest dojeżdżające.

Na przykład dokumentacja Translate metody mówi, że "Wstępnie łączy bieżącą macierz z określonym tłumaczeniem", podczas gdy dokumentacja Scale metody mówi, że "Wstępne łączenie bieżącej macierzy z określoną skalą".

Oznacza to, że przekształcenie określone przez wywołanie metody jest mnożnikiem (operand po lewej stronie), a bieżąca macierz transformacji jest mnożeniem (operand po prawej stronie).

Załóżmy, że Translate nazwa jest wywoływana Scale, a następnie :

canvas.Translate(tx, ty);
canvas.Scale(sx, sy);

Transformacja Scale jest mnożona przez Translate przekształcenie macierzy transformacji złożonej:

| sx   0   0 |   |  1   0   0 |   | sx   0   0 |
|  0  sy   0 | × |  0   1   0 | = |  0  sy   0 |
|  0   0   1 |   | tx  ty   1 |   | tx  ty   1 |

Scale można wywołać przed Translate następującymi nazwami:

canvas.Scale(sx, sy);
canvas.Translate(tx, ty);

W takim przypadku kolejność mnożenia jest odwracana, a czynniki skalowania są skutecznie stosowane do czynników tłumaczenia:

|  1   0   0 |   | sx   0   0 |   |  sx      0    0 |
|  0   1   0 | × |  0  sy   0 | = |   0     sy    0 |
| tx  ty   1 |   |  0   0   1 |   | tx·sx  ty·sy  1 |

Scale Oto metoda z punktem przestawnym:

canvas.Scale(sx, sy, px, py);

Jest to odpowiednik następujących wywołań tłumaczenia i skalowania:

canvas.Translate(px, py);
canvas.Scale(sx, sy);
canvas.Translate(–px, –py);

Trzy macierze przekształcania są mnożone w odwrotnej kolejności od sposobu wyświetlania metod w kodzie:

|  1    0   0 |   | sx   0   0 |   |  1   0  0 |   |    sx         0     0 |
|  0    1   0 | × |  0  sy   0 | × |  0   1  0 | = |     0        sy     0 |
| –px  –py  1 |   |  0   0   1 |   | px  py  1 |   | px–px·sx  py–py·sy  1 |

Struktura SKMatrix

Struktura SKMatrix definiuje dziewięć właściwości odczytu/zapisu typu float odpowiadające dziewięciu komórkom macierzy przekształcania:

│ ScaleX  SkewY   Persp0 │
│ SkewX   ScaleY  Persp1 │
│ TransX  TransY  Persp2 │

SKMatrix Definiuje również właściwość o nazwie Values typu float[]. Tej właściwości można użyć do ustawienia lub uzyskania dziewięciu wartości w jednej kolejności ScaleX, ScaleYTransXSkewXTransYPersp0SkewY, Persp1, i .Persp2

Komórki Persp0, Persp1i Persp2 zostały omówione w artykule Przekształcenia inne niż Affine. Jeśli te komórki mają wartości domyślne 0, 0 i 1, przekształcenie jest mnożone przez punkt współrzędny podobny do następującego:

              │ ScaleX  SkewY   0 │
| x  y  1 | × │ SkewX   ScaleY  0 │ = | x'  y'  z' |
              │ TransX  TransY  1 │

x' = ScaleX · x + SkewX · y + TransX

y' = SkewX · x + ScaleY · y + TransY

z' = 1

Jest to kompletna dwuwymiarowa transformacja affine. Przekształcenie affine zachowuje linie równoległe, co oznacza, że prostokąt nigdy nie jest przekształcany w coś innego niż równoległy.

Struktura SKMatrix definiuje kilka metod statycznych do tworzenia SKMatrix wartości. Te wszystkie zwracane SKMatrix wartości:

• MakeTranslation
• MakeScale
• MakeScale z punktem przestawnym
• MakeRotation kąt w radianach
• MakeRotation kąt w radianach z punktem przestawnym
• MakeRotationDegrees
• MakeRotationDegrees z punktem przestawnym
• MakeSkew

SKMatrix Definiuje również kilka metod statycznych, które łączyją dwie macierze, co oznacza pomnożenie ich. Te metody mają nazwy Concat, PostConcati PreConcat, i istnieją dwie wersje każdego. Te metody nie mają wartości zwracanych; zamiast tego odwołują się do istniejących SKMatrix wartości za pomocą ref argumentów. W poniższym przykładzie wartości A, Bi R (dla "result") to wszystkie SKMatrix wartości.

Dwie Concat metody są wywoływane w następujący sposób:

SKMatrix.Concat(ref R, A, B);

SKMatrix.Concat(ref R, ref A, ref B);

Wykonują one następujące mnożenie:

R = B × A

Inne metody mają tylko dwa parametry. Pierwszy parametr jest modyfikowany, a po powrocie z wywołania metody zawiera produkt dwóch macierzy. Dwie PostConcat metody są wywoływane w następujący sposób:

SKMatrix.PostConcat(ref A, B);

SKMatrix.PostConcat(ref A, ref B);

Te wywołania wykonują następującą operację:

A = A × B

Dwie PreConcat metody są podobne:

SKMatrix.PreConcat(ref A, B);

SKMatrix.PreConcat(ref A, ref B);

Te wywołania wykonują następującą operację:

A = B × A

Wersje tych metod ze wszystkimi ref argumentami są nieco bardziej wydajne w wywoływaniu podstawowych implementacji, ale może to być mylące dla kogoś czytającego kod i zakładając, że wszystkie elementy z argumentem ref są modyfikowane przez metodę . Ponadto często wygodne jest przekazanie argumentu, który jest wynikiem jednej z Make metod, na przykład:

SKMatrix result;
SKMatrix.Concat(result, SKMatrix.MakeTranslation(100, 100),
                        SKMatrix.MakeScale(3, 3));

Spowoduje to utworzenie następującej macierzy:

│   3    0  0 │
│   0    3  0 │
│ 100  100  1 │

Jest to transformacja skali pomnożona przez transformację tłumaczenia. W tym konkretnym przypadku SKMatrix struktura udostępnia skrót z metodą o nazwie SetScaleTranslate:

SKMatrix R = new SKMatrix();
R.SetScaleTranslate(3, 3, 100, 100);

Jest to jeden z niewielu przypadków, kiedy można bezpiecznie użyć konstruktora SKMatrix . Metoda SetScaleTranslate ustawia wszystkie dziewięć komórek macierzy. Można również bezpiecznie używać konstruktora SKMatrix ze statycznymi Rotate metodami i RotateDegrees :

SKMatrix R = new SKMatrix();

SKMatrix.Rotate(ref R, radians);

SKMatrix.Rotate(ref R, radians, px, py);

SKMatrix.RotateDegrees(ref R, degrees);

SKMatrix.RotateDegrees(ref R, degrees, px, py);

Te metody nie łączyją przekształcenia rotacji z istniejącym przekształceniem. Metody ustawiają wszystkie komórki macierzy. Są one funkcjonalnie identyczne z metodami MakeRotation i MakeRotationDegrees , z tą różnicą, że nie tworzą wystąpienia SKMatrix wartości.

Załóżmy, że masz SKPath obiekt, który chcesz wyświetlić, ale wolisz, że ma nieco inną orientację lub inny punkt środkowy. Możesz zmodyfikować wszystkie współrzędne tej ścieżki, wywołując Transform metodę za pomocą argumentu SKPathSKMatrix . Na stronie Przekształcanie ścieżki pokazano, jak to zrobić. Klasa PathTransform odwołuje się do HendecagramPath obiektu w polu, ale używa jego konstruktora do zastosowania przekształcenia do tej ścieżki:

public class PathTransformPage : ContentPage
{
    SKPath transformedPath = HendecagramArrayPage.HendecagramPath;

    public PathTransformPage()
    {
        Title = "Path Transform";

        SKCanvasView canvasView = new SKCanvasView();
        canvasView.PaintSurface += OnCanvasViewPaintSurface;
        Content = canvasView;

        SKMatrix matrix = SKMatrix.MakeScale(3, 3);
        SKMatrix.PostConcat(ref matrix, SKMatrix.MakeRotationDegrees(360f / 22));
        SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(300, 300));

        transformedPath.Transform(matrix);
    }
    ...
}

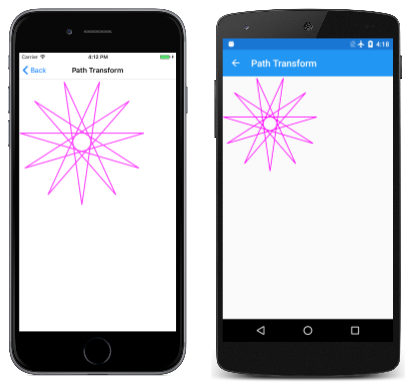
HendecagramPath Obiekt ma środek (0, 0), a 11 punktów gwiazdy rozciąga się na zewnątrz od tego środka o 100 jednostek we wszystkich kierunkach. Oznacza to, że ścieżka ma zarówno współrzędne dodatnie, jak i ujemne. Strona Przekształć ścieżkę preferuje pracę z gwiazdą trzy razy wielokrotnie i ze wszystkimi współrzędnymi dodatnimi. Co więcej, nie chce, aby jeden punkt gwiazdy wskazywał prosto w górę. Zamiast tego chce, aby jeden punkt gwiazdy wskazywał prosto w dół. (Ponieważ gwiazda ma 11 punktów, nie może mieć obu). Wymaga to rotacji gwiazdy o 360 stopni podzielonych przez 22.

Konstruktor tworzy SKMatrix obiekt z trzech oddzielnych przekształceń przy użyciu PostConcat metody z następującym wzorcem, gdzie A, B i C są wystąpieniami SKMatrix:

SKMatrix matrix = A;
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, C);

Jest to seria kolejnych mnożenia, więc wynik jest następujący:

A × B × C

Kolejne mnożenie pomaga zrozumieć, co robi każda transformacja. Przekształcenie skali zwiększa rozmiar współrzędnych ścieżki o współczynnik 3, więc współrzędne wahają się od –300 do 300. Przekształcenie rotacji obraca gwiazdę wokół jej źródła. Przekształcenie translacji następnie przesuwa je o 300 pikseli w prawo i w dół, dzięki czemu wszystkie współrzędne stają się dodatnie.

Istnieją inne sekwencje, które tworzą tę samą macierz. Oto kolejny:

SKMatrix matrix = SKMatrix.MakeRotationDegrees(360f / 22);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(100, 100));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(3, 3));

Najpierw obraca ścieżkę wokół środka, a następnie tłumaczy ją na 100 pikseli po prawej i w dół, dzięki czemu wszystkie współrzędne są dodatnie. Gwiazda jest następnie zwiększana w stosunku do nowego lewego górnego rogu, czyli punktu (0, 0).

Procedura PaintSurface obsługi może po prostu renderować tę ścieżkę:

public class PathTransformPage : ContentPage
{
    ...
    void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
    {
        SKImageInfo info = args.Info;
        SKSurface surface = args.Surface;
        SKCanvas canvas = surface.Canvas;

        canvas.Clear();

        using (SKPaint paint = new SKPaint())
        {
            paint.Style = SKPaintStyle.Stroke;
            paint.Color = SKColors.Magenta;
            paint.StrokeWidth = 5;

            canvas.DrawPath(transformedPath, paint);
        }
    }
}

Zostanie on wyświetlony w lewym górnym rogu kanwy:

Konstruktor tego programu stosuje macierz do ścieżki z następującym wywołaniem:

transformedPath.Transform(matrix);

Ścieżka nie zachowuje tej macierzy jako właściwości. Zamiast tego stosuje przekształcenie do wszystkich współrzędnych ścieżki. Jeśli Transform zostanie ponownie wywołana, przekształcenie zostanie zastosowane ponownie, a jedynym sposobem, w jaki można wrócić, jest zastosowanie innej macierzy, która cofa przekształcenie. Na SKMatrix szczęście struktura definiuje metodę TryInvert , która uzyskuje macierz, która odwraca daną macierz:

SKMatrix inverse;
bool success = matrix.TryInverse(out inverse);

Metoda jest wywoływana TryInverse , ponieważ nie wszystkie macierze są niewzględne, ale macierz niewzględna może być używana do transformacji grafiki.

Można również zastosować przekształcenie macierzy do SKPoint wartości, tablicy punktów, SKRecta nawet tylko jednej liczby w programie. Struktura SKMatrix obsługuje te operacje przy użyciu kolekcji metod rozpoczynających się od słowa Map, takiego jak:

SKPoint transformedPoint = matrix.MapPoint(point);

SKPoint transformedPoint = matrix.MapPoint(x, y);

SKPoint[] transformedPoints = matrix.MapPoints(pointArray);

float transformedValue = matrix.MapRadius(floatValue);

SKRect transformedRect = matrix.MapRect(rect);

Jeśli używasz tej ostatniej metody, pamiętaj, że SKRect struktura nie może reprezentować obróconego prostokąta. Metoda ma sens tylko dla SKMatrix wartości reprezentującej tłumaczenie i skalowanie.

Eksperymentowanie interakcyjne

Jednym ze sposobów uzyskania wrażenia z transformacji affiny jest interaktywne poruszanie się trzema rogami mapy bitowej na ekranie i wyświetlanie wyników transformacji. Jest to idea strony Pokaż macierz Affine. Ta strona wymaga dwóch innych klas, które są również używane w innych demonstracjach:

Klasa TouchPoint wyświetla przezroczysty okrąg, który można przeciągnąć wokół ekranu. TouchPoint wymaga, aby element SKCanvasView lub, który jest elementem nadrzędnym elementu SKCanvasView , miał TouchEffect dołączony element. Ustaw właściwość Capture na true. W procedurze obsługi zdarzeń TouchAction program musi wywołać metodę ProcessTouchEvent in TouchPoint dla każdego TouchPoint wystąpienia. Metoda zwraca true , jeśli zdarzenie dotykowe spowodowało przeniesienie punktu dotykowego. PaintSurface Ponadto program obsługi musi wywołać metodę Paint w każdym TouchPoint wystąpieniuSKCanvas, przekazując do niego obiekt.

TouchPoint demonstruje typowy sposób hermetyzacji wizualizacji SkiaSharp w oddzielnej klasie. Klasa może definiować właściwości określania właściwości wizualizacji, a metoda o nazwie Paint z argumentem SKCanvas może ją renderować.

Właściwość Center wskazuje TouchPoint lokalizację obiektu. Tę właściwość można ustawić, aby zainicjować lokalizację; właściwość zmienia się, gdy użytkownik przeciąga okrąg wokół kanwy.

Strona Pokaż macierz Affine wymaga MatrixDisplay również klasy . Ta klasa wyświetla komórki SKMatrix obiektu. Ma dwie metody publiczne: Measure uzyskiwanie wymiarów renderowanej macierzy i Paint wyświetlanie jej. Klasa zawiera MatrixPaint właściwość typu SKPaint , którą można zamienić na inny rozmiar czcionki lub kolor.

Plik ShowAffineMatrixPage.xaml tworzy wystąpienie SKCanvasView pliku i dołącza element TouchEffect. Plik ShowAffineMatrixPage.xaml.cs za pomocą kodu tworzy trzy TouchPoint obiekty, a następnie ustawia je na pozycje odpowiadające trzem rogom mapy bitowej ładowanej z zasobu osadzonego:

public partial class ShowAffineMatrixPage : ContentPage
{
    SKMatrix matrix;
    SKBitmap bitmap;
    SKSize bitmapSize;

    TouchPoint[] touchPoints = new TouchPoint[3];

    MatrixDisplay matrixDisplay = new MatrixDisplay();

    public ShowAffineMatrixPage()
    {
        InitializeComponent();

        string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
        Assembly assembly = GetType().GetTypeInfo().Assembly;

        using (Stream stream = assembly.GetManifestResourceStream(resourceID))
        {
            bitmap = SKBitmap.Decode(stream);
        }

        touchPoints[0] = new TouchPoint(100, 100);                  // upper-left corner
        touchPoints[1] = new TouchPoint(bitmap.Width + 100, 100);   // upper-right corner
        touchPoints[2] = new TouchPoint(100, bitmap.Height + 100);  // lower-left corner

        bitmapSize = new SKSize(bitmap.Width, bitmap.Height);
        matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
                                           touchPoints[1].Center,
                                           touchPoints[2].Center);
    }
    ...
}

Macierz affine jest unikatowo definiowana przez trzy punkty. Trzy TouchPoint obiekty odpowiadają lewym górnym, prawym górnym i lewym dolnym rogu mapy bitowej. Ponieważ macierz affine jest w stanie przekształcić prostokąt tylko w równoległość, czwarty punkt jest implikowany przez pozostałe trzy. Konstruktor kończy wywołaniem ComputeMatrixmetody , która oblicza komórki SKMatrix obiektu z tych trzech punktów.

Procedura TouchAction obsługi wywołuje metodę ProcessTouchEvent każdego TouchPointelementu . Wartość scale konwertuje Xamarin.Forms z współrzędnych na piksele:

public partial class ShowAffineMatrixPage : ContentPage
{
    ...
    void OnTouchEffectAction(object sender, TouchActionEventArgs args)
    {
        bool touchPointMoved = false;

        foreach (TouchPoint touchPoint in touchPoints)
        {
            float scale = canvasView.CanvasSize.Width / (float)canvasView.Width;
            SKPoint point = new SKPoint(scale * (float)args.Location.X,
                                        scale * (float)args.Location.Y);
            touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
        }

        if (touchPointMoved)
        {
            matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
                                               touchPoints[1].Center,
                                               touchPoints[2].Center);
            canvasView.InvalidateSurface();
        }
    }
    ...
}

Jeśli którykolwiek z nich TouchPoint został przeniesiony, metoda wywołuje ComputeMatrix ponownie i unieważnia powierzchnię.

Metoda ComputeMatrix określa macierz domniemaną przez te trzy punkty. Macierz o nazwie A przekształca prostokąt o jeden piksel kwadratowy w równoległy zależnie od trzech punktów, podczas gdy transformacja skali o nazwie S skaluje mapę bitową do prostokąta kwadratowego o jeden piksel. Macierz złożona jest S × A:

public partial class ShowAffineMatrixPage : ContentPage
{
    ...
    static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL)
    {
        // Scale transform
        SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);

        // Affine transform
        SKMatrix A = new SKMatrix
        {
            ScaleX = ptUR.X - ptUL.X,
            SkewY = ptUR.Y - ptUL.Y,
            SkewX = ptLL.X - ptUL.X,
            ScaleY = ptLL.Y - ptUL.Y,
            TransX = ptUL.X,
            TransY = ptUL.Y,
            Persp2 = 1
        };

        SKMatrix result = SKMatrix.MakeIdentity();
        SKMatrix.Concat(ref result, A, S);
        return result;
    }
    ...
}

PaintSurface Na koniec metoda renderuje mapę bitową na podstawie tej macierzy, wyświetla macierz w dolnej części ekranu i renderuje punkty dotykowe w trzech rogach mapy bitowej:

public partial class ShowAffineMatrixPage : ContentPage
{
    ...
    void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
    {
        SKImageInfo info = args.Info;
        SKSurface surface = args.Surface;
        SKCanvas canvas = surface.Canvas;

        canvas.Clear();

        // Display the bitmap using the matrix
        canvas.Save();
        canvas.SetMatrix(matrix);
        canvas.DrawBitmap(bitmap, 0, 0);
        canvas.Restore();

        // Display the matrix in the lower-right corner
        SKSize matrixSize = matrixDisplay.Measure(matrix);

        matrixDisplay.Paint(canvas, matrix,
            new SKPoint(info.Width - matrixSize.Width,
                        info.Height - matrixSize.Height));

        // Display the touchpoints
        foreach (TouchPoint touchPoint in touchPoints)
        {
            touchPoint.Paint(canvas);
        }
    }
  }

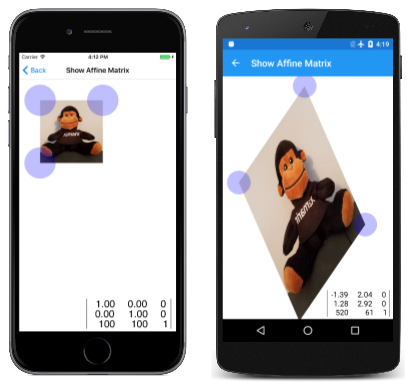
Na poniższym ekranie systemu iOS jest wyświetlana mapa bitowa po pierwszym załadowaniu strony, a dwa inne ekrany pokazują ją po pewnym manipulowaniu:

Chociaż wydaje się, że punkty dotykowe przeciągają rogi mapy bitowej, to tylko iluzja. Macierz obliczana z punktów dotykowych przekształca mapę bitową, tak aby narożniki pokrywały się z punktami dotykowymi.

Bardziej naturalne jest, aby użytkownicy poruszali, zmieniali rozmiar i obracali mapy bitowe, przeciągając rogi, ale przy użyciu jednego lub dwóch palców bezpośrednio na obiekcie w celu przeciągania, szczypania i obracania. Opisano to w następnym artykule Manipulowanie dotykiem.

Przyczyna macierzy 3–3

Można się spodziewać, że dwuwymiarowy system graficzny wymaga tylko macierzy transformacji 2-by-2:

           │ ScaleX  SkewY  │
| x  y | × │                │ = | x'  y' |
           │ SkewX   ScaleY │

Działa to w przypadku skalowania, rotacji, a nawet niesymetryczności, ale nie jest w stanie uzyskać najbardziej podstawowych przekształceń, co jest tłumaczeniem.

Problem polega na tym, że macierz 2-by-2 reprezentuje transformację liniową w dwóch wymiarach. Transformacja liniowa zachowuje niektóre podstawowe operacje arytmetyczne, ale jednym z implikacji jest to, że transformacja liniowa nigdy nie zmienia punktu (0, 0). Transformacja liniowa sprawia, że tłumaczenie jest niemożliwe.

W trzech wymiarach macierz przekształcania liniowego wygląda następująco:

              │ ScaleX  SkewYX  SkewZX │
| x  y  z | × │ SkewXY  ScaleY  SkewZY │ = | x'  y'  z' |
              │ SkewXZ  SkewYZ  ScaleZ │

Komórka oznaczona SkewXY etykietą oznacza, że wartość wypacza współrzędną X na podstawie wartości Y; komórka SkewXZ oznacza, że wartość wypacza współrzędną X na podstawie wartości Z, a wartości niesymetryczne podobnie dla innych Skew komórek.

Można ograniczyć tę macierz przekształcania 3D do płaszczyzny dwuwymiarowej przez ustawienie SkewZX i SkewZY na 0, a ScaleZ do 1:

              │ ScaleX  SkewYX   0 │
| x  y  z | × │ SkewXY  ScaleY   0 │ = | x'  y'  z' |
              │ SkewXZ  SkewYZ   1 │

Jeśli dwuwymiarowa grafika jest rysowana całkowicie na płaszczyźnie w przestrzeni 3D, gdzie Z jest równa 1, mnożenie transformacji wygląda następująco:

              │ ScaleX  SkewYX   0 │
| x  y  1 | × │ SkewXY  ScaleY   0 │ = | x'  y'  1 |
              │ SkewXZ  SkewYZ   1 │

Wszystko pozostaje na dwuwymiarowej płaszczyźnie, gdzie Z równa się 1, ale SkewXZ komórki i SkewYZ skutecznie stają się czynnikami tłumaczeń dwuwymiarowych.

W ten sposób transformacja liniowa trójwymiarowa służy jako dwuwymiarowa transformacja nieliniowa. (Analogicznie przekształcenia w grafice 3D są oparte na macierzy 4-by-4).

Struktura SKMatrix w narzędziu SkiaSharp definiuje właściwości dla tego trzeciego wiersza:

              │ ScaleX  SkewY   Persp0 │
| x  y  1 | × │ SkewX   ScaleY  Persp1 │ = | x'  y'  z` |
              │ TransX  TransY  Persp2 │

Wartości Persp0 inne niż zero i Persp1 powodują przekształcenia, które przenoszą obiekty z płaszczyzny dwuwymiarowej, gdzie Z równa się 1. Co się stanie, gdy te obiekty zostaną przeniesione z powrotem do tej płaszczyzny, zostanie omówione w artykule Dotyczącym przekształceń innych niż Affine.

Linki powiązane

• Interfejsy API skiaSharp