Rotacje 3D w SkiaSharp
Użyj przekształceń innych niż affine, aby obrócić obiekty 2D w przestrzeni 3D.
Jednym z typowych zastosowań przekształceń innych niż affine jest symulowanie obrotu obiektu 2D w przestrzeni 3D:
To zadanie obejmuje pracę z rotacjami trójwymiarowymi, a następnie wyprowadzanie transformacji nieaplikowanej SKMatrix , która wykonuje te rotacje 3D.
Trudno jest opracować tę SKMatrix transformację działającą wyłącznie w dwóch wymiarach. Zadanie staje się znacznie łatwiejsze, gdy ta macierz 3-by-3 pochodzi z macierzy 4-by-4 używanej w grafice 3D. SkiaSharp obejmuje klasę SKMatrix44 do tego celu, ale niektóre tło w grafice 3D jest niezbędne do zrozumienia rotacji 3D i macierzy transformacji 4-po 4.
Trójwymiarowy układ współrzędnych dodaje trzecią oś o nazwie Z. Koncepcyjnie oś Z znajduje się pod kątem prostym na ekranie. Punkty współrzędnych w przestrzeni 3D są wskazywane trzema liczbami: (x, y, z). W systemie współrzędnych 3D używanym w tym artykule zwiększenie wartości X jest na prawo i zwiększenie wartości Y spada, podobnie jak w dwóch wymiarach. Zwiększenie dodatnich wartości Z wychodzi z ekranu. Początek to lewy górny róg, podobnie jak w grafice 2D. Ekran można traktować jako płaszczyznę XY z osią Z pod kątami prostymi do tej płaszczyzny.
Jest to nazywane układem współrzędnych po lewej stronie. Jeśli wskażesz forefinger lewej strony w kierunku dodatnich współrzędnych X (z prawej strony), a środkowy palec w kierunku zwiększenia współrzędnych Y (w dół), to punkty kciuka w kierunku zwiększania współrzędnych Z — rozciągając się od ekranu.
W grafice 3D przekształcenia są oparte na macierzy 4-by-4. Oto macierz tożsamości 4-by-4:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 0 | | 0 0 0 1 |
W pracy z macierzą 4-by-4 wygodnie jest zidentyfikować komórki z ich numerami wierszy i kolumn:
| M11 M12 M13 M14 | | M21 M22 M23 M24 | | M31 M32 M33 M34 | | M41 M42 M43 M44 |
Jednak klasa SkiaSharp Matrix44 jest nieco inna. Jedynym sposobem ustawiania lub pobierania poszczególnych wartości komórek jest SKMatrix44 użycie indeksatora Item . Indeksy wierszy i kolumn są oparte na zera, a nie na podstawie jednej, a wiersze i kolumny są zamieniane. Komórka M14 na powyższym diagramie jest dostępna przy użyciu indeksatora [3, 0]SKMatrix44 w obiekcie.
W systemie graficznym 3D punkt 3D (x, y, z) jest konwertowany na macierz 1-by-4 do mnożenia przez macierz przekształcania 4-by-4:
| M11 M12 M13 M14 |
| x y z 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Analogicznie do przekształceń 2D, które mają miejsce w trzech wymiarach, przyjmuje się, że przekształcenia 3D mają mieć miejsce w czterech wymiarach. Czwarty wymiar jest określany jako W, a przestrzeń 3D zakłada się, że istnieje w przestrzeni 4D, gdzie współrzędne W są równe 1. Formuły przekształcania są następujące:
x' = M11·x + M21·y + M31·z + M41
y' = M12·x + M22·y + M32·z + M42
z' = M13·x + M23·y + M33·z + M43
w' = M14·x + M24·y + M34·z + M44
Z formuł transformacji wynika, że komórki M11, M33M22, są czynnikami skalowania w kierunkach M42M41X, Y i Z oraz , i M43 są czynnikami tłumaczenia w kierunkach X, Y i Z.
Aby przekonwertować te współrzędne z powrotem na przestrzeń 3D, gdzie W równa 1, współrzędne x', y i z są dzielone przez w':
x" = x' / w'
y" = y' / w'
z" = z' / w'
w" = w' / w' = 1
Ten podział według w' zapewnia perspektywę w przestrzeni 3D. Jeśli wartość w jest równa 1, perspektywa nie występuje.
Rotacje w przestrzeni 3D mogą być dość złożone, ale najprostsze rotacje to te wokół osi X, Y i Z. Rotacja kąta α wokół osi X jest następująca macierz:
| 1 0 0 0 | | 0 cos(α) sin(α) 0 | | 0 –sin(α) cos(α) 0 | | 0 0 0 1 |
Wartości X pozostają takie same w przypadku poddania tej transformacji. Obrót wokół osi Y pozostawia wartości Y bez zmian:
| cos(α) 0 –sin(α) 0 | | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 0 1 |
Obrót wokół osi Z jest taki sam jak w grafice 2D:
| cos(α) sin(α) 0 0 | | –sin(α) cos(α) 0 0 | | 0 0 1 0 | | 0 0 0 1 |
Kierunek obrotu jest implikowany przez przekazanie układu współrzędnych. Jest to system leworęczny, więc jeśli wskażesz kciuk lewej ręki w kierunku rosnących wartości dla określonej osi — po prawej stronie dla obrotu wokół osi X, w dół w celu obrotu wokół osi Y, a w kierunku obrotu wokół osi Z — krzywa innych palców wskazuje kierunek obrotu dla kątów dodatnich.
SKMatrix44 ma uogólnione metody statyczne CreateRotation i CreateRotationDegrees , które umożliwiają określenie osi, wokół której odbywa się obrót:
public static SKMatrix44 CreateRotationDegrees (Single x, Single y, Single z, Single degrees)
Dla obrotu wokół osi X ustaw pierwsze trzy argumenty na 1, 0, 0. Dla obrotu wokół osi Y ustaw je na 0, 1, 0 i dla obrotu wokół osi Z, ustaw je na 0, 0, 1.
Czwarta kolumna 4-by-4 jest dla perspektywy. Nie SKMatrix44 ma metod tworzenia przekształceń perspektyw, ale można utworzyć je samodzielnie przy użyciu następującego kodu:
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
Przyczyna nazwy depth argumentu będzie widoczna wkrótce. Ten kod tworzy macierz:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 -1/depth | | 0 0 0 1 |
Formuły przekształcania powodują następujące obliczenie elementu w':
w' = –z / depth + 1
Służy to do zmniejszenia współrzędnych X i Y, gdy wartości Z są mniejsze niż zero (koncepcyjnie za płaszczyzną XY) i zwiększyć współrzędne X i Y dla wartości dodatnich Z. Gdy współrzędna Z równa depth, wartość w' wynosi zero, a współrzędne stają się nieskończone. Trójwymiarowe systemy graficzne są zbudowane wokół metafory aparatu, a depth wartość reprezentuje odległość aparatu od źródła układu współrzędnych. Jeśli obiekt graficzny ma współrzędną Z, która jest depth jednostką pochodzenia, koncepcyjnie dotyka obiektywu aparatu i staje się nieskończenie duża.
Pamiętaj, że prawdopodobnie użyjesz tej perspectiveMatrix wartości w połączeniu z macierzami obrotowymi. Jeśli obracany obiekt graficzny ma współrzędne X lub Y większe niż depth, rotacja tego obiektu w przestrzeni 3D może obejmować współrzędne Z większe niż depth. Należy tego unikać! Podczas tworzenia perspectiveMatrix chcesz ustawić depth wartość wystarczająco dużą dla wszystkich współrzędnych w obiekcie graficznym niezależnie od tego, jak jest obracana. Gwarantuje to, że nigdy nie ma żadnego podziału o zero.
Połączenie obrotu 3D i perspektywy wymaga pomnożenia macierzy 4-by-4 razem. W tym celu SKMatrix44 definiuje metody łączenia. Jeśli A obiekty i B są SKMatrix44 obiektami, następujący kod ustawia wartość A równą A × B:
A.PostConcat(B);
Gdy macierz przekształcania 4-by-4 jest używana w systemie graficznym 2D, jest stosowana do obiektów 2D. Te obiekty są płaskie i zakłada się, że współrzędnych Z wynosi zero. Mnożenie transformacji jest nieco prostsze niż pokazana wcześniej transformacja:
| M11 M12 M13 M14 |
| x y 0 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Ta wartość 0 dla z powoduje przekształcenie formuł, które nie obejmują żadnych komórek w trzecim wierszu macierzy:
x' = M11·x + M21·y + M41
y' = M12·x + M22·y + M42
z' = M13·x + M23·y + M43
w' = M14·x + M24·y + M44
Co więcej, współrzędna z również nie ma znaczenia tutaj. Gdy obiekt 3D jest wyświetlany w systemie graficznym 2D, jest zwinięty do obiektu dwuwymiarowego, ignorując wartości współrzędnych Z. Formuły przekształcania są naprawdę tylko tymi dwoma:
x" = x' / w'
y" = y' / w'
Oznacza to, że trzeci wiersz i trzecia kolumna macierzy 4-by-4 mogą być ignorowane.
Ale jeśli tak jest, dlaczego macierz 4-by-4 jest nawet niezbędna w pierwszej kolejności?
Mimo że trzeci wiersz i trzecia kolumna 4-by-4 są nieistotne dla przekształceń dwuwymiarowych, trzeci wiersz i kolumna odgrywają rolę przed tym, gdy różne SKMatrix44 wartości są mnożone razem. Załóżmy na przykład, że pomnożysz rotację wokół osi Y za pomocą przekształcenia perspektywy:
| cos(α) 0 –sin(α) 0 | | 1 0 0 0 | | cos(α) 0 –sin(α) sin(α)/depth | | 0 1 0 0 | × | 0 1 0 0 | = | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 1 -1/depth | | sin(α) 0 cos(α) -cos(α)/depth | | 0 0 0 1 | | 0 0 0 1 | | 0 0 0 1 |
W produkcie komórka M14 zawiera teraz wartość perspektywy. Jeśli chcesz zastosować tę macierz do obiektów 2D, trzeci wiersz i kolumna zostaną wyeliminowane, aby przekonwertować ją na macierz 3-by-3:
| cos(α) 0 sin(α)/depth | | 0 1 0 | | 0 0 1 |
Teraz można go użyć do przekształcenia punktu 2D:
| cos(α) 0 sin(α)/depth |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
Formuły przekształcania to:
x' = cos(α)·x
y' = y
z' = (sin(α)/depth)·x + 1
Teraz podziel wszystko przez z':
x" = cos(α)·x / ((sin(α)/depth)·x + 1)
y" = y / ((sin(α)/depth)·x + 1)
Gdy obiekty 2D są obracane z dodatnim kątem wokół osi Y, wartości dodatnie X cofają się do tła, podczas gdy ujemne wartości X przychodzą na pierwszy plan. Wartości X wydają się zbliżać do osi Y (która jest określana przez wartość cosinus) jako współrzędne najdalej z osi Y staje się mniejsza lub większa, gdy przesuwają się dalej z przeglądarki lub bliżej osoby przeglądającego.
W przypadku korzystania z programu SKMatrix44wykonaj wszystkie operacje obrotu 3D i perspektywy, mnożąc różne SKMatrix44 wartości. Następnie można wyodrębnić dwuwymiarową macierz 3-by-3 z macierzy 4-by-4 przy użyciu Matrix właściwości SKMatrix44 klasy . Ta właściwość zwraca znaną SKMatrix wartość.
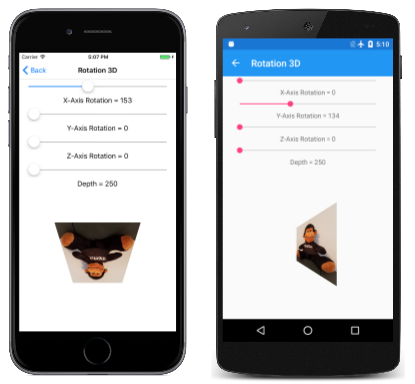
Strona Rotacja 3D umożliwia eksperymentowanie z rotacją 3D . Plik Rotation3DPage.xaml tworzy cztery suwaki, aby ustawić obrót wokół osi X, Y i Z oraz ustawić wartość głębokości:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.Rotation3DPage"
Title="Rotation 3D">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Margin" Value="20, 0" />
<Setter Property="Maximum" Value="360" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="xRotateSlider"
Grid.Row="0"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference xRotateSlider},
Path=Value,
StringFormat='X-Axis Rotation = {0:F0}'}"
Grid.Row="1" />
<Slider x:Name="yRotateSlider"
Grid.Row="2"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference yRotateSlider},
Path=Value,
StringFormat='Y-Axis Rotation = {0:F0}'}"
Grid.Row="3" />
<Slider x:Name="zRotateSlider"
Grid.Row="4"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference zRotateSlider},
Path=Value,
StringFormat='Z-Axis Rotation = {0:F0}'}"
Grid.Row="5" />
<Slider x:Name="depthSlider"
Grid.Row="6"
Maximum="2500"
Minimum="250"
ValueChanged="OnSliderValueChanged" />
<Label Grid.Row="7"
Text="{Binding Source={x:Reference depthSlider},
Path=Value,
StringFormat='Depth = {0:F0}'}" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="8"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Zwróć uwagę, że element depthSlider jest inicjowany z wartością Minimum 250. Oznacza to, że obracany w tym miejscu obiekt 2D ma współrzędne X i Y ograniczone do okręgu zdefiniowanego przez promień 250 pikseli wokół źródła. Każda rotacja tego obiektu w przestrzeni 3D zawsze spowoduje współrzędnych wartości mniejszych niż 250.
Plik Rotation3DPage.cs za pomocą kodu ładuje się w mapie bitowej, która ma 300 pikseli kwadratowych:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
...
}
Jeśli transformacja 3D jest wyśrodkowana na tej mapie bitowej, współrzędne X i Y wahają się od –150 do 150, podczas gdy narożniki są 212 pikseli od środka, więc wszystko znajduje się w promieniu 250 pikseli.
Procedura PaintSurface obsługi tworzy SKMatrix44 obiekty na podstawie suwaków i mnoży je razem przy użyciu polecenia PostConcat. SKMatrix Wartość wyodrębniona z obiektu końcowego SKMatrix44 jest otoczona przetłumaczeniami, aby wyśrodkować obrót w środku ekranu:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Use 3D matrix for 3D rotations and perspective
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, (float)xRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, (float)yRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, (float)zRotateSlider.Value));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / (float)depthSlider.Value;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the bitmap
canvas.SetMatrix(matrix);
float xBitmap = xCenter - bitmap.Width / 2;
float yBitmap = yCenter - bitmap.Height / 2;
canvas.DrawBitmap(bitmap, xBitmap, yBitmap);
}
}
Podczas eksperymentowania z czwartym suwakiem zauważysz, że różne ustawienia głębokości nie przenoszą obiektu dalej od przeglądarki, ale zmieniają zakres efektu perspektywy:
Animowany obrót 3D używa SKMatrix44 również do animowania ciągu tekstowego w przestrzeni 3D. Obiekt textPaint ustawiony jako pole jest używany w konstruktorze w celu określenia granic tekstu:
public class AnimatedRotation3DPage : ContentPage
{
SKCanvasView canvasView;
float xRotationDegrees, yRotationDegrees, zRotationDegrees;
string text = "SkiaSharp";
SKPaint textPaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
TextSize = 100,
StrokeWidth = 3,
};
SKRect textBounds;
public AnimatedRotation3DPage()
{
Title = "Animated Rotation 3D";
canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
// Measure the text
textPaint.MeasureText(text, ref textBounds);
}
...
}
Przesłonięcia OnAppearing definiują trzy Xamarin.FormsAnimation obiekty, aby animować xRotationDegreespola , yRotationDegreesi zRotationDegrees w różnych stawkach. Zwróć uwagę, że okresy tych animacji są ustawione na liczby pierwsze (5 sekund, 7 sekund i 11 sekund), więc ogólna kombinacja powtarza się tylko co 385 sekund lub więcej niż 10 minut:
public class AnimatedRotation3DPage : ContentPage
{
...
protected override void OnAppearing()
{
base.OnAppearing();
new Animation((value) => xRotationDegrees = 360 * (float)value).
Commit(this, "xRotationAnimation", length: 5000, repeat: () => true);
new Animation((value) => yRotationDegrees = 360 * (float)value).
Commit(this, "yRotationAnimation", length: 7000, repeat: () => true);
new Animation((value) =>
{
zRotationDegrees = 360 * (float)value;
canvasView.InvalidateSurface();
}).Commit(this, "zRotationAnimation", length: 11000, repeat: () => true);
}
protected override void OnDisappearing()
{
base.OnDisappearing();
this.AbortAnimation("xRotationAnimation");
this.AbortAnimation("yRotationAnimation");
this.AbortAnimation("zRotationAnimation");
}
...
}
Podobnie jak w poprzednim programie program PaintCanvas obsługi tworzy SKMatrix44 wartości dla rotacji i perspektywy i mnoży je razem:
public class AnimatedRotation3DPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Scale so text fits
float scale = Math.Min(info.Width / textBounds.Width,
info.Height / textBounds.Height);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(scale, scale));
// Calculate composite 3D transforms
float depth = 0.75f * scale * textBounds.Width;
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, xRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, yRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, zRotationDegrees));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the text
canvas.SetMatrix(matrix);
float xText = xCenter - textBounds.MidX;
float yText = yCenter - textBounds.MidY;
canvas.DrawText(text, xText, yText, textPaint);
}
}
Ta rotacja 3D jest otoczona kilkoma transformacjami 2D, aby przenieść środek obrotu do środka ekranu i skalować rozmiar ciągu tekstowego, tak aby była taka sama szerokość jak ekran: