Opracowywanie, ocena i punktowanie modelu prognozowania sprzedaży hipermarketu
Ten samouczek przedstawia pełny przykład przepływu pracy analizy danych usługi Synapse w usłudze Microsoft Fabric. Scenariusz tworzy model prognozowania, który używa historycznych danych sprzedaży do przewidywania sprzedaży kategorii produktów w superstore.
Prognozowanie jest kluczowym elementem w sprzedaży. Łączy ona dane historyczne i metody predykcyjne, aby zapewnić wgląd w przyszłe trendy. Prognozowanie umożliwia analizowanie przeszłości sprzedaży w celu identyfikowania wzorców i poznawania zachowań konsumentów w celu optymalizacji strategii spisu, produkcji i marketingu. To proaktywne podejście zwiększa elastyczność, czas reakcji i ogólną wydajność firm na dynamicznym rynku.
W tym samouczku opisano następujące kroki:
- Ładowanie danych
- Korzystanie z eksploracyjnej analizy danych w celu zrozumienia i przetworzenia danych
- Trenuj model uczenia maszynowego przy użyciu pakietu oprogramowania open-source i śledź eksperymenty za pomocą MLflow oraz funkcji autologowania Fabric.
- Zapisywanie końcowego modelu uczenia maszynowego i przewidywanie
- Wyświetlanie wydajności modelu za pomocą wizualizacji usługi Power BI
Warunki wstępne
Pobierz subskrypcję usługi Microsoft Fabric . Możesz też utworzyć bezpłatne konto wersji próbnej usługi Microsoft Fabric.
Zaloguj się do usługi Microsoft Fabric.
Użyj przełącznika doświadczenia w lewej dolnej części strony głównej, aby przełączyć się na Fabric.
- W razie potrzeby utwórz magazyn lakehouse usługi Microsoft Fabric zgodnie z opisem w Tworzenie magazynu lakehouse w usłudze Microsoft Fabric.
Notuj w zeszycie
Możesz wybrać jedną z tych opcji, aby korzystać z niej w notatniku:
- Otwieranie i uruchamianie wbudowanego notatnika w doświadczeniu Synapse Data Science.
- Prześlij swój notes z usługi GitHub do środowiska nauki o danych usługi Synapse
Otwieranie wbudowanego notesu
Przykładowy notatnik Sales forecasting towarzyszy temu samouczkowi.
Aby otworzyć przykładowy notes na potrzeby tego samouczka, postępuj zgodnie z instrukcjami w Przygotuj swój system do samouczków z zakresu nauki o danych.
Przed rozpoczęciem uruchamiania kodu upewnij się, że dołączyć magazyn lakehouse do notesu.
Importowanie notatnika z GitHub
Ten samouczek zawiera notes AIsample — Superstore Forecast.ipynb.
Aby otworzyć towarzyszący notatnik na potrzeby tego samouczka, postępuj zgodnie z instrukcjami w Prepare your system for data science tutorials (Przygotuj swój system do samouczków dotyczących nauki o danych), aby zaimportować notatnik do obszaru roboczego.
Jeśli wolisz skopiować i wkleić kod z tej strony, możesz utworzyć nowy notes.
Przed rozpoczęciem uruchamiania kodu pamiętaj, aby dołączyć lakehouse do notesu.
Krok 1. Ładowanie danych
Zestaw danych zawiera 9995 wystąpień sprzedaży różnych produktów. Zawiera również 21 atrybutów. Ta tabela pochodzi z pliku Superstore.xlsx używanego w tym notesie:
| ID wiersza | Identyfikator zamówienia | Data zamówienia | Data wysyłki | Tryb wysyłki | Identyfikator klienta | Nazwa klienta | Segment | Kraj | Miasto | Stan | Kod pocztowy | Region | Identyfikator produktu | Kategoria | Sub-Category | Nazwa produktu | Sprzedaż | Ilość | Rabat | Zysk |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | USA-2015-108966 | 2015-10-11 | 2015-10-18 | Klasa standardowa | SO-20335 | Sean O'Donnell | Konsument | Stany Zjednoczone | Fort Lauderdale | Floryda | 33311 | Południe | FUR-TA-10000577 | Meble | Tabele | Bretford CR4500 Seria Slim Prostokątny Stół | 957,5775 | 5 | 0.45 | -383.0310 |
| 11 | CA-2014-115812 | 2014-06-09 | 2014-06-09 | Klasa standardowa | Klasa standardowa | Brosina Hoffman | Konsument | Stany Zjednoczone | Los Angeles | Kalifornia | 90032 | Zachód | FUR-TA-10001539 | Meble | Tabele | Stoły konferencyjne prostokątne Chromcraft | 1706.184 | 9 | 0.2 | 85.3092 |
| 31 | USA-2015-150630 | 2015-09-17 | 2015-09-21 | Klasa standardowa | TB-21520 | Tracy Blumstein | Konsument | Stany Zjednoczone | Filadelfia | Pensylwania | 19140 | Wschód | OFF-EN-10001509 | Materiały biurowe | Koperty | Koperty zamykane na sznurek | 3.264 | 2 | 0.2 | 1.1016 |
Zdefiniuj te parametry, aby można było używać tego notesu z różnymi zestawami danych:
IS_CUSTOM_DATA = False # If TRUE, the dataset has to be uploaded manually
IS_SAMPLE = False # If TRUE, use only rows of data for training; otherwise, use all data
SAMPLE_ROWS = 5000 # If IS_SAMPLE is True, use only this number of rows for training
DATA_ROOT = "/lakehouse/default"
DATA_FOLDER = "Files/salesforecast" # Folder with data files
DATA_FILE = "Superstore.xlsx" # Data file name
EXPERIMENT_NAME = "aisample-superstore-forecast" # MLflow experiment name
Pobierz zbiór danych i prześlij do Lakehouse
Ten kod pobiera publicznie dostępną wersję zestawu danych, a następnie przechowuje go w usłudze Fabric Lakehouse:
Ważny
Przed uruchomieniem należy dodać lakehouse do notatnika. W przeciwnym razie zostanie wyświetlony błąd.
import os, requests
if not IS_CUSTOM_DATA:
# Download data files into the lakehouse if they're not already there
remote_url = "https://synapseaisolutionsa.blob.core.windows.net/public/Forecast_Superstore_Sales"
file_list = ["Superstore.xlsx"]
download_path = "/lakehouse/default/Files/salesforecast/raw"
if not os.path.exists("/lakehouse/default"):
raise FileNotFoundError(
"Default lakehouse not found, please add a lakehouse and restart the session."
)
os.makedirs(download_path, exist_ok=True)
for fname in file_list:
if not os.path.exists(f"{download_path}/{fname}"):
r = requests.get(f"{remote_url}/{fname}", timeout=30)
with open(f"{download_path}/{fname}", "wb") as f:
f.write(r.content)
print("Downloaded demo data files into lakehouse.")
Konfigurowanie śledzenia eksperymentów MLflow
Usługa Microsoft Fabric automatycznie przechwytuje wartości parametrów wejściowych i metryk wyjściowych modelu uczenia maszynowego podczas jego trenowania. Rozszerza to funkcje automatycznego rejestrowania MLflow. Informacje są następnie rejestrowane w obszarze roboczym, gdzie można uzyskać do niego dostęp i zwizualizować je za pomocą interfejsów API platformy MLflow lub odpowiedniego eksperymentu w obszarze roboczym. Aby dowiedzieć się więcej na temat autologowania, patrz Autologowanie w Microsoft Fabric.
Aby wyłączyć automatyczne rejestrowanie w Microsoft Fabric w sesji notatnika, wywołaj mlflow.autolog() i ustaw disable=True:
# Set up MLflow for experiment tracking
import mlflow
mlflow.set_experiment(EXPERIMENT_NAME)
mlflow.autolog(disable=True) # Turn off MLflow autologging
Odczytywanie danych surowych z lakehouse
Odczytywanie danych surowych z sekcji Files lakehouse. Dodaj więcej kolumn dla różnych części daty. Te same informacje są używane do tworzenia partycjonowanej tabeli Delta. Ponieważ dane pierwotne są przechowywane jako plik programu Excel, należy użyć biblioteki pandas, aby je odczytać:
import pandas as pd
df = pd.read_excel("/lakehouse/default/Files/salesforecast/raw/Superstore.xlsx")
Krok 2. Wykonywanie eksploracyjnej analizy danych
Importowanie bibliotek
Przed rozpoczęciem analizy zaimportuj wymagane biblioteki:
# Importing required libraries
import warnings
import itertools
import numpy as np
import matplotlib.pyplot as plt
warnings.filterwarnings("ignore")
plt.style.use('fivethirtyeight')
import pandas as pd
import statsmodels.api as sm
import matplotlib
matplotlib.rcParams['axes.labelsize'] = 14
matplotlib.rcParams['xtick.labelsize'] = 12
matplotlib.rcParams['ytick.labelsize'] = 12
matplotlib.rcParams['text.color'] = 'k'
from sklearn.metrics import mean_squared_error,mean_absolute_percentage_error
Wyświetlanie danych pierwotnych
Ręcznie przejrzyj podzbiór danych, aby lepiej zrozumieć sam zestaw danych i użyć funkcji display do wydrukowania ramki danych. Ponadto widoki Chart mogą łatwo wizualizować podzestawy zestawu danych.
display(df)
Ten notatnik koncentruje się głównie na prognozowaniu sprzedaży dla kategorii Furniture. Przyspiesza to obliczanie i pomaga pokazać wydajność modelu. Jednak w tym notatniku używane są techniki dostosowywalne. Możesz rozszerzyć te techniki, aby przewidzieć sprzedaż innych kategorii produktów.
# Select "Furniture" as the product category
furniture = df.loc[df['Category'] == 'Furniture']
print(furniture['Order Date'].min(), furniture['Order Date'].max())
Wstępne przetwarzanie danych
Rzeczywiste scenariusze biznesowe często muszą przewidywać sprzedaż w trzech różnych kategoriach:
- Określona kategoria produktu
- Określona kategoria klienta
- Określona kombinacja kategorii produktów i kategorii klientów
Najpierw upuść niepotrzebne kolumny, aby wstępnie przetworzyć dane. Niektóre kolumny (Row ID, Order ID,Customer IDi Customer Name) są niepotrzebne, ponieważ nie mają wpływu. Chcemy prognozować ogólną sprzedaż w całym stanie i regionie dla określonej kategorii produktów (Furniture), abyśmy mogli usunąć kolumny State, Region, Country, Cityi Postal Code. Aby prognozować sprzedaż dla określonej lokalizacji lub kategorii, może być konieczne odpowiednie dostosowanie kroku przetwarzania wstępnego.
# Data preprocessing
cols = ['Row ID', 'Order ID', 'Ship Date', 'Ship Mode', 'Customer ID', 'Customer Name',
'Segment', 'Country', 'City', 'State', 'Postal Code', 'Region', 'Product ID', 'Category',
'Sub-Category', 'Product Name', 'Quantity', 'Discount', 'Profit']
# Drop unnecessary columns
furniture.drop(cols, axis=1, inplace=True)
furniture = furniture.sort_values('Order Date')
furniture.isnull().sum()
Zestaw danych jest codziennie ustrukturyzowany. Musimy ponownie próbkować kolumnę Order Date, ponieważ chcemy opracować model prognozowania sprzedaży na podstawie miesięcznej.
Najpierw pogrupuj kategorię Furniture według Order Date. Następnie oblicz sumę kolumny Sales dla każdej grupy, aby określić łączną sprzedaż dla każdej unikatowej wartości Order Date. Przepróbkuj kolumnę Sales przy użyciu częstotliwości MS, aby agregować dane na miesiące. Na koniec oblicz średnią wartość sprzedaży dla każdego miesiąca.
# Data preparation
furniture = furniture.groupby('Order Date')['Sales'].sum().reset_index()
furniture = furniture.set_index('Order Date')
furniture.index
y = furniture['Sales'].resample('MS').mean()
y = y.reset_index()
y['Order Date'] = pd.to_datetime(y['Order Date'])
y['Order Date'] = [i+pd.DateOffset(months=67) for i in y['Order Date']]
y = y.set_index(['Order Date'])
maximim_date = y.reset_index()['Order Date'].max()
Zademonstrowanie wpływu Order Date na Sales dla kategorii Furniture:
# Impact of order date on the sales
y.plot(figsize=(12, 3))
plt.show()
Przed rozpoczęciem analizy statystycznej należy zaimportować moduł statsmodels Python. Udostępnia klasy i funkcje do szacowania wielu modeli statystycznych. Udostępnia również klasy i funkcje do przeprowadzania testów statystycznych i eksploracji danych statystycznych.
import statsmodels.api as sm
Przeprowadzanie analizy statystycznej
Szereg czasowy śledzi te elementy danych w ustalonych odstępach czasu, aby określić odmianę tych elementów we wzorcu szeregów czasowych:
poziom: podstawowy składnik reprezentujący średnią wartość dla określonego okresu
trend: opisuje, czy szereg czasowy zmniejsza się, pozostaje stały lub zwiększa się w czasie
sezonowość: opisuje okresowy sygnał w szeregach czasowych i wyszukuje cykliczne wystąpienia wpływające na rosnące lub malejące wzorce szeregów czasowych
Szum/Reszty: odnosi się do losowych wahań i zmienności danych serii czasowej, których model nie może wyjaśnić.
W tym kodzie obserwujesz te elementy dla zestawu danych po wstępnym przetwarzaniu:
# Decompose the time series into its components by using statsmodels
result = sm.tsa.seasonal_decompose(y, model='additive')
# Labels and corresponding data for plotting
components = [('Seasonality', result.seasonal),
('Trend', result.trend),
('Residual', result.resid),
('Observed Data', y)]
# Create subplots in a grid
fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(12, 7))
plt.subplots_adjust(hspace=0.8) # Adjust vertical space
axes = axes.ravel()
# Plot the components
for ax, (label, data) in zip(axes, components):
ax.plot(data, label=label, color='blue' if label != 'Observed Data' else 'purple')
ax.set_xlabel('Time')
ax.set_ylabel(label)
ax.set_xlabel('Time', fontsize=10)
ax.set_ylabel(label, fontsize=10)
ax.legend(fontsize=10)
plt.show()
Wykresy opisują sezonowość, trendy i szumy w danych prognozowania. Możesz przechwytywać podstawowe wzorce i opracowywać modele, które tworzą dokładne przewidywania odporne na losowe wahania.
Krok 3. Trenowanie i śledzenie modelu
Teraz, gdy masz dostępne dane, zdefiniuj model prognozowania. W tym notesie zastosuj model prognozowania o nazwie sezonowy autoregresyjny zintegrowany model średniej ruchomej z czynnikami egzogenicznymi (SARIMAX). SARIMAX łączy składniki autoregresywne (AR) i średniej ruchomej (MA), sezonowe różnice i zewnętrzne predyktory, aby zapewnić dokładne i elastyczne prognozy dla danych szeregów czasowych.
Aby śledzić eksperymenty, używasz również automatycznego rejestrowania MLflow i Fabric autologging. Tutaj załaduj tabelę delty z lakehouse. Możesz użyć innych tabel różnicowych, które traktują lakehouse jako źródło.
# Import required libraries for model evaluation
from sklearn.metrics import mean_squared_error, mean_absolute_percentage_error
Dostrajanie hiperparametrów
SARIMAX uwzględnia parametry w trybie regularnym autoregresyjnej zintegrowanej średniej ruchomej (ARIMA) (p, d, q), i dodaje parametry sezonowości (P, D, Q, s). Argumenty modelu SARIMAX nazywane są rząd (p, d, q) i sezonowy rząd (P, D, Q, s), odpowiednio. W związku z tym, aby wytrenować model, musimy najpierw dostroić siedem parametrów.
Parametry zamówienia:
p: kolejność składnika AR reprezentująca liczbę wcześniejszych obserwacji w szeregach czasowych używanych do przewidywania bieżącej wartości.Zazwyczaj ten parametr powinien być nieujemną liczbą całkowitą. Wspólne wartości znajdują się w zakresie
0do3, chociaż możliwe są wyższe wartości, w zależności od określonych cech danych. Wyższapwartość wskazuje dłuższą pamięć poprzednich wartości w modelu.d: Rząd różnicowania, reprezentujący liczbę razy, ile szeregi czasowe muszą być różnicowane, aby osiągnąć stacjonarność.Ten parametr powinien być nieujemną liczbą całkowitą. Typowe wartości znajdują się w zakresie
0do2. Wartośćd0oznacza, że szereg czasowy jest już stacjonarny. Wyższe wartości wskazują liczbę operacji różnicowych wymaganych, aby uczynić go stacjonarnym.q: kolejność składnika MA, reprezentująca liczbę poprzednich błędów szumu białego używanych do przewidywania bieżącej wartości.Ten parametr powinien być nieujemną liczbą całkowitą. Typowe wartości znajdują się w zakresie
0do3, ale w przypadku niektórych szeregów czasowych mogą być konieczne wyższe wartości. Wyższa wartośćqwskazuje na silniejszą zależność od błędów z przeszłości w celu przewidywania.
Parametry zamówienia sezonowego:
-
P: kolejność sezonowa składnika AR, podobna dopale dla części sezonowej -
D: sezonowa kolejność różnic, podobna dod, ale dla części sezonowej -
Q: sezonowa kolejność składnika MA podobna doq, ale dla części sezonowej -
s: liczba kroków czasu na cykl sezonowy (na przykład 12 dla danych miesięcznych z roczną sezonowością)
# Hyperparameter tuning
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
print('Examples of parameter combinations for Seasonal ARIMA...')
print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[1]))
print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[2]))
print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[3]))
print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[4]))
SARIMAX ma inne parametry:
enforce_stationarity: Czy model powinien wymuszać stacjonarność na danych szeregów czasowych przed dopasowaniem modelu SARIMAX.Jeśli
enforce_stationarityjest ustawiona naTrue(wartość domyślna), oznacza to, że model SARIMAX powinien wymuszać stacjonarność na danych szeregów czasowych. Następnie model SARIMAX automatycznie stosuje różnicowanie w danych, aby zniwelować zmienność, zgodnie ze stopniamidiD, przed dopasowaniem modelu. Jest to powszechna praktyka, ponieważ wiele modeli szeregów czasowych, w tym SARIMAX, zakłada, że dane są nieruchome.W przypadku niestacjonarnych szeregów czasowych (na przykład, gdy wykazują trendy lub sezonowość), dobrym rozwiązaniem jest ustawienie
enforce_stationaritynaTruei pozwolenie modelowi SARIMAX na przeprowadzenie różnicowania, aby uzyskać stacjonarność. W przypadku stacjonarnych szeregów czasowych (na przykład bez trendów lub sezonowości) ustawenforce_stationaritynaFalse, aby uniknąć niepotrzebnych różnic.enforce_invertibility: Określa, czy model powinien wymuszać odwracalność na szacowanych parametrach podczas procesu optymalizacji.Jeśli
enforce_invertibilityjest ustawione na wartośćTrue(wartość domyślna), oznacza to, że model SARIMAX powinien wymuszać odwracalność na szacowanych parametrach. Odwracalność gwarantuje, że model jest dobrze zdefiniowany oraz że szacowane współczynniki AR i MA znajdują się w zakresie stacjonarności.Wymuszanie właściwości odwracalności pomaga zapewnić, że model SARIMAX jest zgodny z teoretycznymi wymaganiami stabilności modelu szeregów czasowych. Pomaga również zapobiegać problemom z szacowaniem modelu i stabilnością.
Wartość domyślna to model AR(1). Dotyczy to (1, 0, 0). Typowym rozwiązaniem jest jednak wypróbowanie różnych kombinacji parametrów zamówienia i parametrów zamówienia sezonowego oraz ocena wydajności modelu dla zestawu danych. Odpowiednie wartości mogą się różnić od jednej serii czasowej do innej.
Określenie optymalnych wartości często obejmuje analizę funkcji autokorelacji (ACF) i częściowej funkcji autokorelacji (PACF) danych szeregów czasowych. Często wiąże się to również z zastosowaniem kryteriów wyboru modelu — na przykład kryterium informacyjnego Akaike (AIC) lub kryterium informacyjnego Bayesa (BIC).
Dostrajanie hiperparametrów:
# Tune the hyperparameters to determine the best model
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(y,
order=param,
seasonal_order=param_seasonal,
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit(disp=False)
print('ARIMA{}x{}12 - AIC:{}'.format(param, param_seasonal, results.aic))
except:
continue
Po dokonaniu oceny powyższych wyników można określić wartości zarówno parametrów zamówienia, jak i parametrów zamówienia sezonowego. Wybór to order=(0, 1, 1) i seasonal_order=(0, 1, 1, 12), które oferują najniższą AIC (na przykład 279,58). Użyj tych wartości, aby wytrenować model.
Trenowanie modelu
# Model training
mod = sm.tsa.statespace.SARIMAX(y,
order=(0, 1, 1),
seasonal_order=(0, 1, 1, 12),
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit(disp=False)
print(results.summary().tables[1])
Ten kod wizualizuje prognozę szeregów czasowych dla danych sprzedaży mebli. Nakreślone wyniki pokazują zarówno obserwowane dane, jak i jednodniową prognozę, z zacienionym obszarem dla przedziału ufności.
# Plot the forecasting results
pred = results.get_prediction(start=maximim_date, end=maximim_date+pd.DateOffset(months=6), dynamic=False) # Forecast for the next 6 months (months=6)
pred_ci = pred.conf_int() # Extract the confidence intervals for the predictions
ax = y['2019':].plot(label='observed')
pred.predicted_mean.plot(ax=ax, label='One-step ahead forecast', alpha=.7, figsize=(12, 7))
ax.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], color='k', alpha=.2)
ax.set_xlabel('Date')
ax.set_ylabel('Furniture Sales')
plt.legend()
plt.show()
# Validate the forecasted result
predictions = results.get_prediction(start=maximim_date-pd.DateOffset(months=6-1), dynamic=False)
# Forecast on the unseen future data
predictions_future = results.get_prediction(start=maximim_date+ pd.DateOffset(months=1),end=maximim_date+ pd.DateOffset(months=6),dynamic=False)
Użyj predictions, aby ocenić wydajność modelu, kontrastując z rzeczywistymi wartościami. Wartość predictions_future wskazuje przyszłe prognozowanie.
# Log the model and parameters
model_name = f"{EXPERIMENT_NAME}-Sarimax"
with mlflow.start_run(run_name="Sarimax") as run:
mlflow.statsmodels.log_model(results,model_name,registered_model_name=model_name)
mlflow.log_params({"order":(0,1,1),"seasonal_order":(0, 1, 1, 12),'enforce_stationarity':False,'enforce_invertibility':False})
model_uri = f"runs:/{run.info.run_id}/{model_name}"
print("Model saved in run %s" % run.info.run_id)
print(f"Model URI: {model_uri}")
mlflow.end_run()
# Load the saved model
loaded_model = mlflow.statsmodels.load_model(model_uri)
Krok 4. Generowanie wyników modelu i zapisywanie przewidywań
Zintegruj rzeczywiste wartości z prognozowanymi wartościami, aby utworzyć raport usługi Power BI. Zapisz te wyniki w tabeli w lakehouse.
# Data preparation for Power BI visualization
Future = pd.DataFrame(predictions_future.predicted_mean).reset_index()
Future.columns = ['Date','Forecasted_Sales']
Future['Actual_Sales'] = np.NAN
Actual = pd.DataFrame(predictions.predicted_mean).reset_index()
Actual.columns = ['Date','Forecasted_Sales']
y_truth = y['2023-02-01':]
Actual['Actual_Sales'] = y_truth.values
final_data = pd.concat([Actual,Future])
# Calculate the mean absolute percentage error (MAPE) between 'Actual_Sales' and 'Forecasted_Sales'
final_data['MAPE'] = mean_absolute_percentage_error(Actual['Actual_Sales'], Actual['Forecasted_Sales']) * 100
final_data['Category'] = "Furniture"
final_data[final_data['Actual_Sales'].isnull()]
input_df = y.reset_index()
input_df.rename(columns = {'Order Date':'Date','Sales':'Actual_Sales'}, inplace=True)
input_df['Category'] = 'Furniture'
input_df['MAPE'] = np.NAN
input_df['Forecasted_Sales'] = np.NAN
# Write back the results into the lakehouse
final_data_2 = pd.concat([input_df,final_data[final_data['Actual_Sales'].isnull()]])
table_name = "Demand_Forecast_New_1"
spark.createDataFrame(final_data_2).write.mode("overwrite").format("delta").save(f"Tables/{table_name}")
print(f"Spark DataFrame saved to delta table: {table_name}")
Krok 5. Wizualizowanie w usłudze Power BI
Raport usługi Power BI przedstawia średni bezwzględny błąd procentowy (MAPE) 16,58. Metryka MAPE definiuje dokładność metody prognozowania. Reprezentuje dokładność prognozowanych ilości, w porównaniu z rzeczywistymi ilościami.
MAPE to prosta metryka. 10% MAPE oznacza, że średnie odchylenie między prognozowanych wartości i wartości rzeczywistych wynosi 10%, niezależnie od tego, czy odchylenie było dodatnie, czy ujemne. Standardy pożądanych wartości MAPE różnią się w różnych branżach.
Jasnoniebieska linia na tym wykresie reprezentuje rzeczywiste wartości sprzedaży. Ciemnoniebieska linia reprezentuje prognozowane wartości sprzedaży. Porównanie rzeczywistej i prognozowanej sprzedaży pokazuje, że model skutecznie przewiduje sprzedaż dla kategorii Furniture w ciągu pierwszych sześciu miesięcy 2023 r.
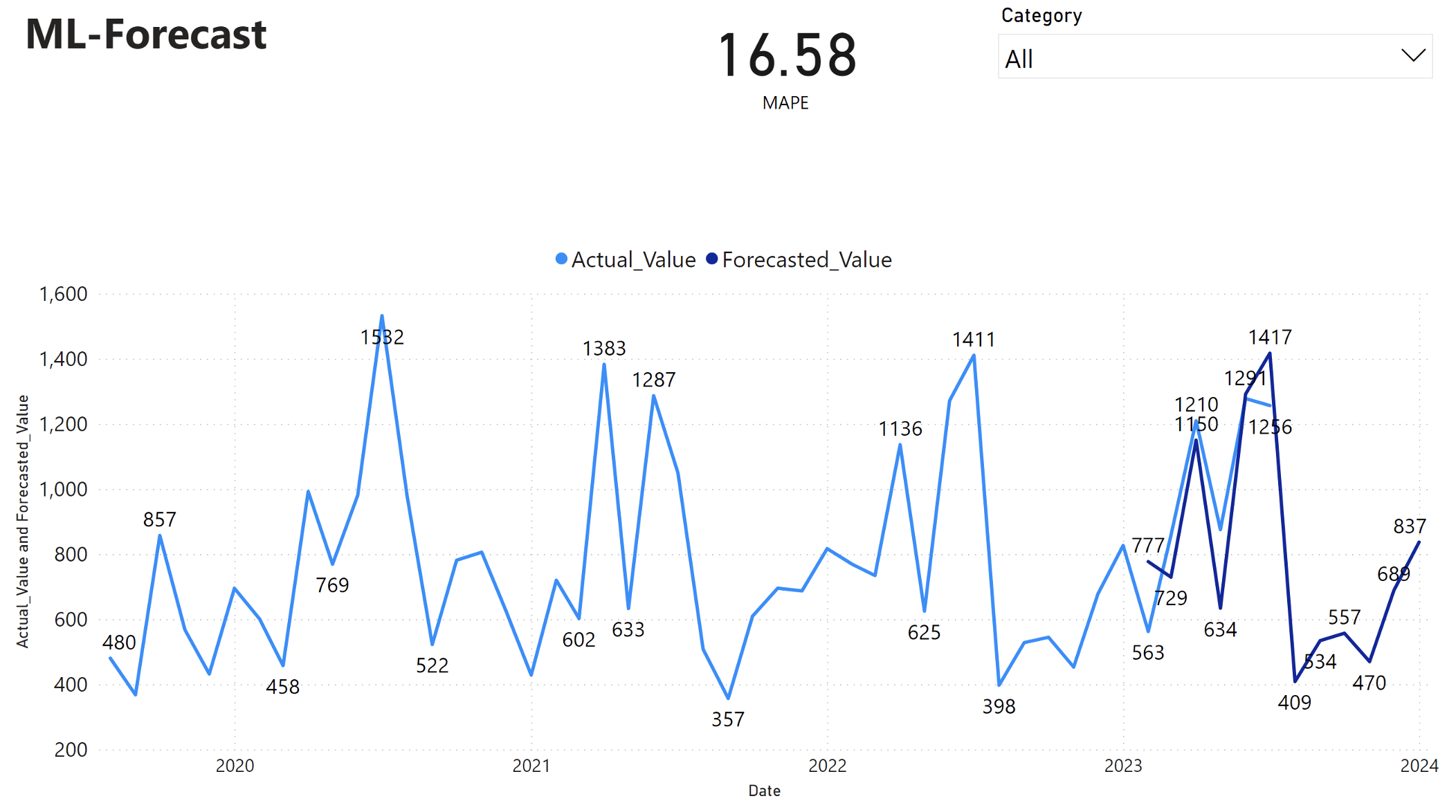
Na podstawie tej obserwacji możemy mieć pewność, że możliwości prognozowania modelu są oparte na ogólnej sprzedaży w ciągu ostatnich sześciu miesięcy 2023 r. i rozszerzają się na rok 2024. To zaufanie może informować o strategicznych decyzjach dotyczących zarządzania zapasami, zaopatrzenia w surowce i innych zagadnień związanych z działalnością biznesową.