Teoria algorytmu wyszukiwania Grovera

W tym artykule znajdziesz szczegółowe teoretyczne wyjaśnienie zasad matematycznych, które sprawiają, że algorytm Grovera działa.

Aby zapoznać się z praktyczną implementacją algorytmu Grovera w celu rozwiązywania problemów matematycznych, zobacz Implementowanie algorytmu wyszukiwania Grovera.

Stwierdzenie problemu

Algorytm Grovera przyspiesza rozwiązanie wyszukiwania danych bez struktury (lub problem z wyszukiwaniem), uruchamiając wyszukiwanie w mniejszej liczbie kroków niż jakikolwiek algorytm klasyczny. Każde zadanie wyszukiwania można wyrazić za pomocą funkcji $abstrakcyjnej f(x),$ która akceptuje elementy $wyszukiwania x$. Jeśli element $x$ jest rozwiązaniem zadania wyszukiwania, $f(x)=1$. Jeśli element $x$ nie jest rozwiązaniem, $f(x)=0$. Problem z wyszukiwaniem polega na znalezieniu dowolnego elementu $x_0$ tak, aby $f(x_0)=1$.

Rzeczywiście, każdy problem, który pozwala sprawdzić, czy dana wartość $x$ jest prawidłowym rozwiązaniem (cudzysłów &; Tak lub nie ma problemu&;) można sformułować w kategoriach problemu wyszukiwania. Poniżej przedstawiono kilka przykładów:

• Problem z satyfikowaniem wartości logicznych: czy zestaw wartości $logicznych x$ interpretacja (przypisanie wartości do zmiennych), która spełnia daną formułę logiczną?
• Problem sprzedawcy podróży: Czy $x$ opisuje najkrótszą możliwą pętlę, która łączy wszystkie miasta?
• Problem z wyszukiwaniem bazy danych: czy tabela bazy danych zawiera rekord $x$?
• Problem z faktoryzacji liczb całkowitych: czy stała liczba $N$ jest podzielna przez liczbę $x$?

Zadanie, które ma na celu algorytm Grovera, można wyrazić w następujący sposób: biorąc pod uwagę klasyczną funkcję $f(x):\{0,1\}^n \rightarrow\{0,1\}$, gdzie $n$ jest rozmiarem bitowym przestrzeni wyszukiwania, znajdź dane wejściowe $x_0$ , dla których $f(x_0)=1$. Złożoność algorytmu jest mierzona przez liczbę zastosowań funkcji $f(x)$. Klasycznie, w najgorszym scenariuszu, $f(x)$ musi zostać obliczona suma $N-1$ razy, gdzie $N=2^n$, próbując wszystkie możliwości. Po $N-1$ element musi być ostatnim elementem. Algorytm kwantowy Grovera może rozwiązać ten problem znacznie szybciej, zapewniając szybkość kwadratową. W tym miejscu kwadrans oznacza, że wymagane byłyby tylko $\sqrt{wartości N}$ w porównaniu z $N$.

Konspekt algorytmu

Załóżmy, że istnieją $n=2^n$ kwalifikujących się elementów do zadania wyszukiwania i są one indeksowane przez przypisanie każdej jednostki całkowitej z zakresu od $0$ do $N-1$. Ponadto załóżmy, że istnieją $różne prawidłowe dane wejściowe języka M$ , co oznacza, że istnieją $dane wejściowe języka M$ , dla których $f(x)=1$. Następnie kroki algorytmu są następujące:

1. Zacznij od rejestru $n$ kubitów zainicjowanych w stanie $\ket{0}$.
2. Przygotuj rejestr do jednolitej superpozycji, stosując $H do każdego kubitu rejestru: $$|\text{zarejestruj}\rangle=\frac{1}{\sqrt{N\sum}}_{x=0}^{N-1}|$ x\rangle$$
3. Zastosuj następujące operacje do N_{\text{optymalnych}}$ czasów rejestracji$:
   1. Wyrocznia $fazowa O_f$ , która stosuje przesunięcie $fazy warunkowej -1$ dla elementów rozwiązania.
   2. Zastosuj $H$ do każdego kubitu w rejestrze.
   3. Przesunięcie fazy warunkowej $-1$ na każdy stan podstawy obliczeniowej z wyjątkiem $\ket{0}$. Może to być reprezentowane przez operację $jednostkową -O_0$, ponieważ $O_0$ reprezentuje przesunięcie fazy warunkowej tylko na $\ket{0}$ .
   4. Zastosuj $H$ do każdego kubitu w rejestrze.
4. Zmierz rejestr, aby uzyskać indeks elementu, który jest rozwiązaniem z bardzo wysokim prawdopodobieństwem.
5. Sprawdź, czy jest to prawidłowe rozwiązanie. Jeśli nie, uruchom ponownie.

$\text{N_optymalny\left=}\lfloor \frac{\pi}{{4}\sqrt{\frac{N M}{}}-{2}\frac{1}{\right\rfloor$ jest optymalną liczbą iteracji, która maksymalizuje prawdopodobieństwo uzyskania prawidłowego elementu przez pomiar rejestru.

Uwaga

Wspólne stosowanie kroków 3.b, 3.c i 3.d jest zwykle znane w literaturze jako operator dyfuzji Grovera.

Ogólna operacja jednostkowa zastosowana do rejestru to:

$$(-H^{\otimes n}O_0H^ n}O_f)^{\otimes{N_{\text{optymalny}}}H^{\otimes n}$$

Krok po kroku po stanie rejestracji

Aby zilustrować ten proces, postępujmy zgodnie z matematycznymi przekształceniami stanu rejestru dla prostego przypadku, w którym istnieją tylko dwa kubity, a prawidłowym elementem jest $\ket{01}.$

1. Rejestr rozpoczyna się w stanie: $$|\text{zarejestruj}\rangle=|00\rangle$$

2. Po zastosowaniu $H$ do każdego kubitu stan rejestru przekształca się w: $$|\text{register{1}{\sqrt{=\frac{}\rangle{4}}\sum_{i \in \{0,1\}^2 i\rangle=\frac12}|(\ket{00}+\ket{01}++)\ket{10}\ket{11}$$

3. Następnie wyrocznia fazowa jest stosowana w celu uzyskania: $$|\text{zarejestruj}\rangle\frac=się 12(\ket{{00}-\ket{{01}++)\ket{{10}\ket{{11}$$

4. Następnie $H$ ponownie działa na każdym kubitie, aby dać: $$|\text{zarejestruj}\rangle\frac=12(\ket{{00}+\ket{{01}-{10}\ket{+)\ket{{11}$$

5. Teraz przesunięcie fazy warunkowej jest stosowane w każdym stanie z wyjątkiem$\ket{00}$: $$|\text{register}\rangle\frac=12(\ket{{00}-+\ket{{01}{10}\ket{-)\ket{{11}$$

6. Na koniec pierwsza iteracja Grovera kończy się zastosowaniem $H$ ponownie, aby uzyskać: $$|\text{zarejestruj}\rangle=\ket{{01}$$

   Wykonując powyższe kroki, prawidłowy element znajduje się w pojedynczej iteracji. Jak zobaczysz później, jest to spowodowane tym, że dla N=4 i jednego prawidłowego elementu, $N_\text{optymalny}=1$.

Wyjaśnienie geometryczne

Aby zobaczyć, dlaczego algorytm Grovera działa, przeanalizujmy algorytm z geometrycznej perspektywy. Niech $\ket{\text{źle}}$ jest superpozycją wszystkich stanów, które nie są rozwiązaniem problemu wyszukiwania. Załóżmy, że istnieją $prawidłowe rozwiązania M$ :

$$\ket{\text{bad}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$

Dobry stan $\ket{\text{}}$ jest definiowany jako superpozycja wszystkich stanów, które są rozwiązaniem problemu wyszukiwania:

$$\ket{\text{good}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$

Ponieważ dobre i złe są wzajemnie wykluczające się zestawy, ponieważ element nie może być prawidłowy i nieprawidłowy, stany $\ket{\text{dobre}}$ i $\ket{\text{złe}}$ są ortogonalne. Oba stany tworzą ortogonalną podstawę płaszczyzny w przestrzeni wektorowej. Można użyć tej płaszczyzny do wizualizacji algorytmu.

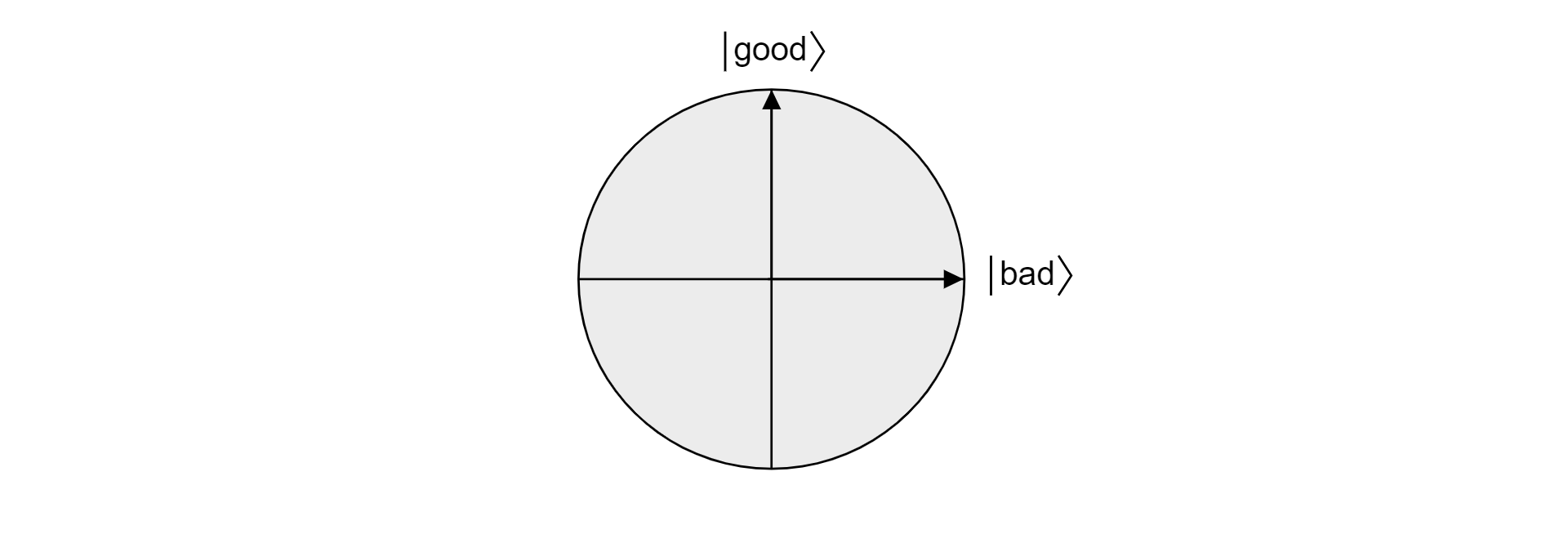
Załóżmy, że $\ket{\psi}$ jest to dowolny stan, który mieszka w samolocie otoczony przez $\ket{\text{dobre}}$ i $\ket{\text{złe}}$. Każdy stan mieszkający w tym samolocie może być wyrażony jako:

$$\ket{\psi}=\alpha\ket{\text{dobre}} + \beta\ket{\text{złe}}$$

gdzie $\alpha$ i $\beta$ są liczbami rzeczywistymi. Teraz przedstawimy operator $odbicia R_{\ket{\psi}}$, gdzie $\ket{\psi}$ jest dowolnym stanem kubitu mieszkającym w samolocie. Operator jest zdefiniowany jako:

$${\ket{\psi}}=R_2\ket{\psi}\bra{\psi}-\mathcal{I}$$

Jest on nazywany operatorem odbicia, $\ket{\psi}$ ponieważ można go geometrycznie interpretować jako odbicie kierunku $\ket{\psi}$. Aby to zobaczyć, weź ortogonalną podstawę płaszczyzny utworzonej przez $\ket{\psi}$ i jego ortogonalny dopełnienie $\ket{\psi^{\perp}}$. Każdy stan $\ket{\xi}$ płaszczyzny można rozkładać w taki sposób:

$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$

Jeśli jeden z nich stosuje operator $R_{\ket{\psi}}$ do $\ket{\xi}$:

$${\ket{\psi}}\ket{R_\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$

Operator $R_\ket{\psi}$ odwraca składnik ortogonal do $\ket{\psi}$ , ale pozostawia $\ket{\psi}$ składnik bez zmian. $W związku z tym R_\ket{\psi}$ jest refleksją na temat $\ket{\psi}$.

Algorytm Grovera, po pierwszym zastosowaniu H$ do każdego kubitu$, zaczyna się od jednolitej superpozycji wszystkich stanów. Można to napisać jako:

$$\ket{\text{wszystkie}}\sqrt{\frac{=M}{N}}\ket{\text{dobre + \sqrt{\frac{N-M}{N}}\ket{\text{złe}}}}$$

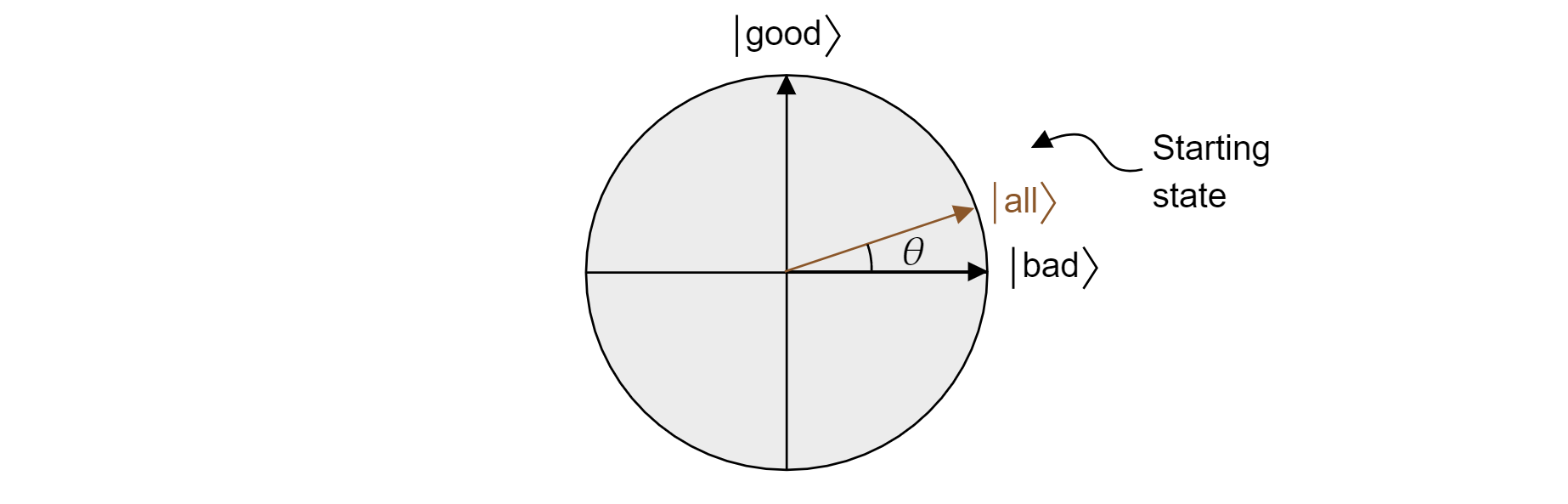
A tym samym państwo mieszka w samolocie. Należy pamiętać, że prawdopodobieństwo uzyskania poprawnego wyniku podczas pomiaru z równej superpozycji jest po prostu $|\braket{\text{dobre}|{\text{wszystkie}}}|^2=M/N$, co można oczekiwać od losowego zgadnięcia.

Wyrocznia $O_f$ dodaje fazę ujemną do dowolnego rozwiązania problemu wyszukiwania. W związku z tym można go napisać jako odbicie o złej $\ket{\text{}}$ osi:

$$= O_f R_{\ket{\text{bad=}}} 2\ket{\text{złe}}\bra{\text{}} - \mathcal{I}$$

Analogicznie, przesunięcie $fazy warunkowej O_0$ jest po prostu odwróconym odbiciem stanu $\ket{0}$:

$$O_0 R_{\ket{0}}= -2\ket{{0}\bra{0} + \mathcal{I =}$$

Znając ten fakt, łatwo jest sprawdzić, czy operacja $dyfuzji Grovera -H^ n} O_0 H^{\otimes{\otimes n}$ jest również odzwierciedleniem stanu $\ket{wszystkiego}$. Po prostu wykonaj:

$$-H^{\otimes n} O_0 H^{\otimes n}=2H^ n H^{\otimes{0}}\ket{0}\bra{ n} -H{\otimes^{\otimes n}\mathcal I}H^{\otimes n=} 2\ket{\text{wszystkie}}\bra{\text{}} - \mathcal{{I}= R_all{\ket{\text{}}}$$

Wykazano, że każda iteracja algorytmu Grovera jest kompozycją dwóch odbić $R_\ket{\text{bad}}$ i $R_\ket{\text{all}}$.

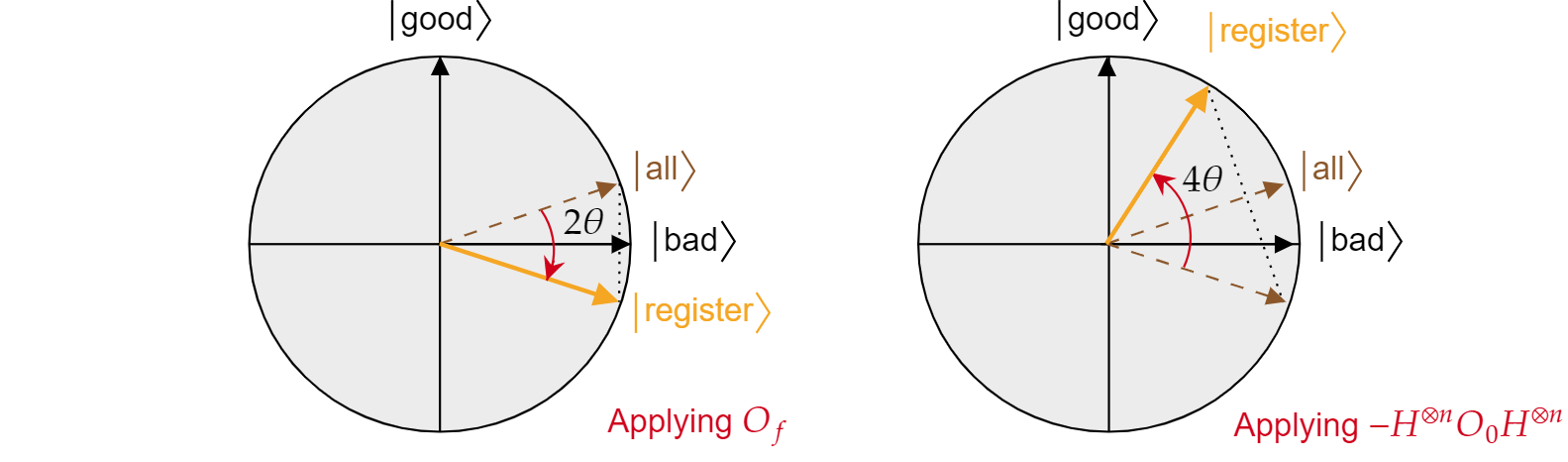
Łączny efekt każdej iteracji Grovera to obrót w kierunku przeciwkręcanym kąta $2\theta$. Na szczęście kąt $\theta$ jest łatwy do znalezienia. Ponieważ $\theta$ jest tylko kątem między $\ket{\text{wszystkimi}}$ i $\ket{\text{złymi}}$, można użyć produktu skalarnego, aby znaleźć kąt. Wiadomo, że $\cos{\theta}=\braket{\text{wszystkie}|\text{złe}}$, więc należy obliczyć $\braket{\text{wszystkie}|\text{złe}}$. Z dekompozycji wszystkich}}$ pod względem złego}}$ i $\ket{\text{dobrego}}$$\ket{\text{$\ket{\text{ następuje:

$$\theta = \arccos(\braket{\text{wszystkie}|\text{złe}}\right)}= \arccos{\left{\left(\sqrt{\frac{N-M}{N}}\right)}$$

Kąt między stanem rejestru a $\ket{\text{dobrym}}$ stanem zmniejsza się wraz z każdą iterację, co powoduje wyższe prawdopodobieństwo pomiaru prawidłowego wyniku. Aby obliczyć to prawdopodobieństwo, wystarczy obliczyć $|\braket{\text{dobry}|\text{rejestr}}|^2$. Oznaczanie kąta między wartością dobrą a rejestrem}}$$\gamma (k)$, gdzie $k$ jest liczbą iteracji:$\ket{\text{}}$ $\ket{\text{

$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$

W związku z tym prawdopodobieństwo sukcesu jest następujące:

$$P(\text{success}) = \cos^2(k\gamma)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$

Optymalna liczba iteracji

Ponieważ prawdopodobieństwo sukcesu można napisać jako funkcję liczby iteracji, optymalna liczba iteracji $N_{\text{optymalna}}$ można znaleźć, obliczając najmniejszą dodatnią liczbę całkowitą, która (w przybliżeniu) maksymalizuje funkcję prawdopodobieństwa sukcesu.

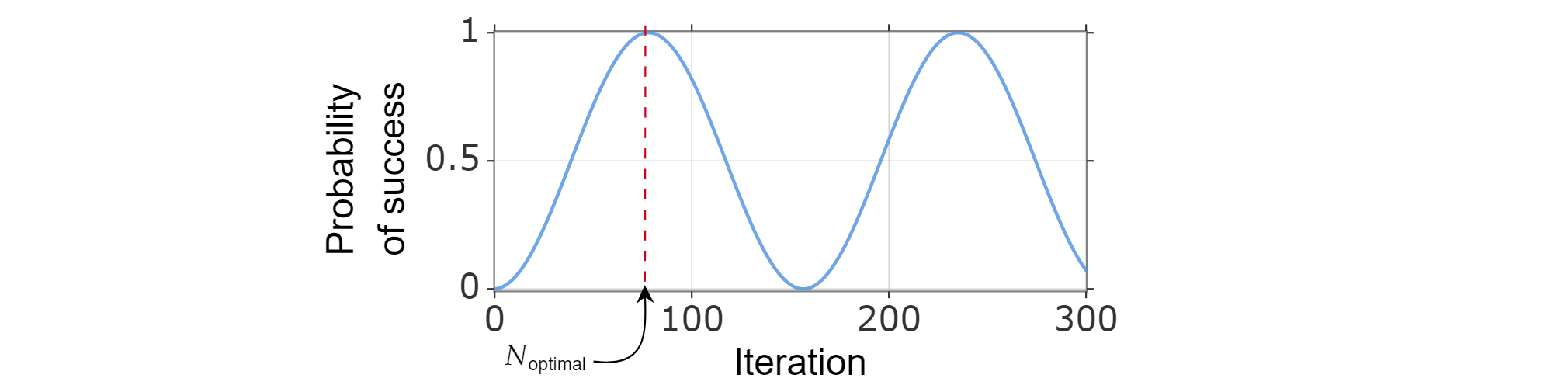
Wiadomo, że $\sin^2{x}$ osiąga pierwszą maksymalną wartość dla $x=\frac{\pi}{2}$, więc:

$$\frac{\pi}{{2}=(2k_{\text{optymalny}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$

Daje to:

$${\text{k_optymalny=\frac{}}\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 =\frac{\pi{4}\sqrt{\frac{}{N}}}{--\frac{1}{2}O\left(\sqrt\frac{M}{N)}\right$$

Gdzie w ostatnim kroku $\arccos \sqrt{1-x=\sqrt{}x} + O(x^{3/2})$.

W związku z tym można wybrać N_optymalny, aby być $N_\text{\text{optymalny\left=}\lfloor \frac{\pi{4}\sqrt{\frac{}{N}{M}}-{1}{2}\frac{\right\rfloor.$}$ $

Analiza złożoności

Z poprzedniej analizy $zapytania O\left(\sqrt{\frac{N}{M}}\right)$ wyroczni $O_f$ są potrzebne do znalezienia prawidłowego elementu. Jednak czy algorytm można skutecznie zaimplementować pod względem złożoności czasu? $$ O_0 opiera się na przetwarzaniu operacji logicznych na $n$ bitach i jest znany jako możliwy do zaimplementowania przy użyciu $bram O(n).$ Istnieją również dwie warstwy $bram n$ Hadamard. Oba te składniki wymagają zatem tylko $bram O(n)$ na iterację. Ponieważ $N=2^n$ następuje, że $O(n)O(log(N)=))$. W związku z tym jeśli $są potrzebne iteracji O\left(\sqrt{\frac{N}{M}}\right)$ i $bramy O(log(N)) na iterację, łączna złożoność czasu (bez uwzględniania implementacji wyroczni)$ to $O\left(\sqrt{\frac{N M}}log(N}{)))\right).$.

Ogólna złożoność algorytmu zależy ostatecznie od złożoności implementacji wyroczni $O_f$. Jeśli ocena funkcji jest znacznie bardziej skomplikowana na komputerze kwantowym niż w klasycznym, ogólny czas wykonywania algorytmu będzie dłuższy w przypadku kwantowym, mimo że technicznie używa mniejszej liczby zapytań.

Informacje

Jeśli chcesz kontynuować naukę o algorytmie Grovera, możesz sprawdzić dowolne z następujących źródeł:

• Oryginalny papier Lov K. Grover
• Sekcja Algorytmy wyszukiwania kwantowego w nielsen, M. A. &Amp; Chuang, I. L. (2010). Obliczenia kwantowe i informacje kwantowe.
• Algorytm Grovera na Arxiv.org

Powiązana zawartość

• Splątanie w obliczeniach kwantowych
• Wektory i macierze
• Bramy T i fabryki T
• Wiele kubitów