De rol van T-poorten en T-factory's in kwantumcomputing
In dit artikel wordt de rol van T-poorten en T-factory's in fouttolerante kwantumcomputing beschreven. Door een kwantumalgoritmen te geven, wordt de schatting van de vereiste resources voor het uitvoeren van de T-poorten en T-factory's cruciaal om de haalbaarheid van het algoritme te bepalen. De Azure Quantum Resource Estimator berekent het aantal T-statussen dat nodig is om het algoritme uit te voeren, het aantal fysieke qubits voor één T-factory en de runtime van de T-factory.
Universele set kwantumpoorten
Volgens de criteria van DiVincenzo moet een schaalbare kwantumcomputer een universele set kwantumpoorten kunnen implementeren. Een universele set bevat alle poorten die nodig zijn om kwantumberekeningen uit te voeren, dat wil gezegd dat elke berekening weer moet worden opgesplitst in een eindige reeks universele poorten. Ten minste moet een kwantumcomputer enkele qubits kunnen verplaatsen naar elke positie op de Bloch Sphere (met behulp van enkele qubitpoorten), en verstrengeling in het systeem introduceren, waarvoor een multi-qubitpoort is vereist.
Er zijn slechts vier functies die één bit toewijzen aan één bit op een klassieke computer. Daarentegen zijn er een oneindig aantal eenheidstransformaties op één qubit op een kwantumcomputer. Daarom kan geen eindige set primitieve kwantumbewerkingen of poorten exact de oneindige set eenheidstransformaties repliceren die zijn toegestaan in kwantumcomputing. Dit betekent dat, in tegenstelling tot klassieke computing, het onmogelijk is voor een kwantumcomputer om elk mogelijk kwantumprogramma exact te implementeren met behulp van een eindig aantal poorten. Kwantumcomputers kunnen dus niet universeel zijn in dezelfde zin van klassieke computers. Als we zeggen dat een set poorten universeel is voor kwantumcomputing, bedoelen we eigenlijk iets zwakker dan we bedoelen met klassieke computing.
Voor universaliteit is het vereist dat een kwantumcomputer alleen elke eenheidsmatrix binnen een eindige fout bij benadering benadert met behulp van een eindige lengtepoortvolgorde.
Met andere woorden, een set poorten is een universele poortset als een eenheidstransformatie ongeveer kan worden geschreven als een product van poorten uit deze set. Het is vereist dat er voor elke voorgeschreven foutgrens poorten $bestaan G_{1}, G_{2}, \ldots, G_N$ van de poortset zodanig dat
$${G_N G_N-1}\cdots G_2 G_1 \ca. U.$$
Omdat de conventie voor matrixververmenigvuldigen is om te vermenigvuldigen van rechts naar links de eerste poortbewerking in deze reeks, $G_N$, is eigenlijk de laatste die wordt toegepast op de kwantumstatusvector. Formeel gezegd is een dergelijke poortset universeel als er voor elke fouttolerantie $\epsilon>0$ bestaat $G_1, \ldots, G_N$ zodanig dat de afstand tussen $G_N\ldots G_1$ en $U$ ten hoogste $\epsilon$ is. In het ideale geval moet de waarde van $N$ die nodig is om deze afstand van $\epsilon$ te bereiken poly-logaritmetisch schalen met $1/\epsilon$.
De set die wordt gevormd door Hadamard-, CNOT- en T-poorten is bijvoorbeeld een universele set, waaruit elke kwantumberekening (op een willekeurig aantal qubits) kan worden gegenereerd. De Hadamard en de T-gateset genereren een enkele qubitpoort:
$$H=\frac{1}{\sqrt{ 1 amp; 1 1 \\ &-1\end{bmatrix}, \qquad T=\begin{bmatrix} 1 & 0 0 \\ & e^{i\pi/4.\end{bmatrix}}&{2}}\begin{bmatrix} $$
In een kwantumcomputer kunnen kwantumpoorten worden geclassificeerd in twee categorieën: Clifford-poorten en niet-Clifford-poorten, in dit geval de T-poort. Kwantumprogramma's die zijn gemaakt van alleen Clifford-poorten kunnen efficiënt worden gesimuleerd met behulp van een klassieke computer, en daarom zijn niet-Clifford-poorten vereist om kwantumvoordelen te verkrijgen. In veel QEC-schema's (Kwantumfoutcorrectie) zijn de zogenaamde Clifford-poorten eenvoudig te implementeren, dat wil gezegd dat ze zeer weinig resources nodig hebben in termen van bewerkingen en qubits om fouttolerantie te implementeren, terwijl niet-Clifford-poorten behoorlijk kostbaar zijn wanneer fouttolerantie vereist is. In een universele kwantumpoortset wordt de T-poort vaak gebruikt als de niet-Clifford-poort.
De standaardset single-qubit Clifford-poorten, standaard opgenomen in Q#, include
$$H=\frac{{2}}\begin{bmatrix}{1}{\sqrt{ 1 & 1 1 \\ &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 0 \\ & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 \\ 1& 0 \end{bmatrix}= HT^4H,$$
$$Y =0 amp; -i i&\\; 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1&&\begin{bmatrix} 0\\ 0&-1 \end{bmatrix}=T^4. $$
Samen met de niet-Clifford-poort (de T-poort) kunnen deze bewerkingen worden samengesteld om elke eenheidstransformatie op één qubit te benaderen.
T-factory's in de Azure Quantum Resource Estimator
De voorbereiding van de niet-Clifford T-poort is cruciaal omdat de andere kwantumpoorten niet voldoende zijn voor universele kwantumberekeningen. Voor het implementeren van niet-Clifford-bewerkingen voor praktische algoritmen is een lage foutfrequentie T-poorten (of T-statussen) vereist. Ze kunnen echter moeilijk rechtstreeks worden geïmplementeerd op logische qubits en kunnen ook moeilijk zijn voor sommige fysieke qubits.
In een fouttolerante kwantumcomputer worden de vereiste lage foutsnelheid T-staten geproduceerd met behulp van een T-statusdestillatiefabriek of T-fabriek kortom. Deze T-fabrieken hebben meestal betrekking op een reeks rondes van distillatie, waarbij elke ronde veel lawaaierige T-staten in een kleinere afstandscode verwerkt, ze verwerkt met behulp van een distillatie-eenheid en minder luidruchtige T-staten die zijn gecodeerd in een grotere afstandscode, met het aantal rondes, distillatie-eenheden en afstanden die allemaal parameters zijn die kunnen worden gevarieerd. Deze procedure wordt curseerd, waarbij de uitvoer-T-statussen van één ronde worden ingevoerd in de volgende ronde als invoer.
Op basis van de duur van de T-factory bepaalt de Azure Quantum Resource Estimator hoe vaak een T-factory kan worden aangeroepen voordat deze de totale runtime van het algoritme overschrijdt, en dus hoeveel T-statussen kunnen worden geproduceerd tijdens de algoritmeruntime. Normaal gesproken zijn er meer T-statussen vereist dan wat tijdens de algoritmeruntime kan worden geproduceerd binnen de aanroepen van één T-factory. Om meer T-statussen te produceren, gebruikt de resource-estimator kopieën van de T-factory's.
Fysieke schatting van T Factory
De resource-estimator berekent het totale aantal T-statussen dat nodig is om het algoritme uit te voeren en het aantal fysieke qubits voor één T-factory en de runtime.
Het doel is om alle T-statussen binnen de algoritmeruntime te produceren met zo weinig mogelijk exemplaren van T Factory. In het volgende diagram ziet u een voorbeeld van de runtime van het algoritme en de runtime van één T-factory. U kunt zien dat de runtime van de T-factory korter is dan de runtime van het algoritme. In dit voorbeeld kan één T-fabriek één T-status destilleren. Er zijn twee vragen:
- Hoe vaak kan de T-factory vóór het einde van het algoritme worden aangeroepen?
- Hoeveel exemplaren van de T-fabrieksdestillatieronde zijn nodig om het aantal T-statussen te maken dat is vereist tijdens de runtime van het algoritme?
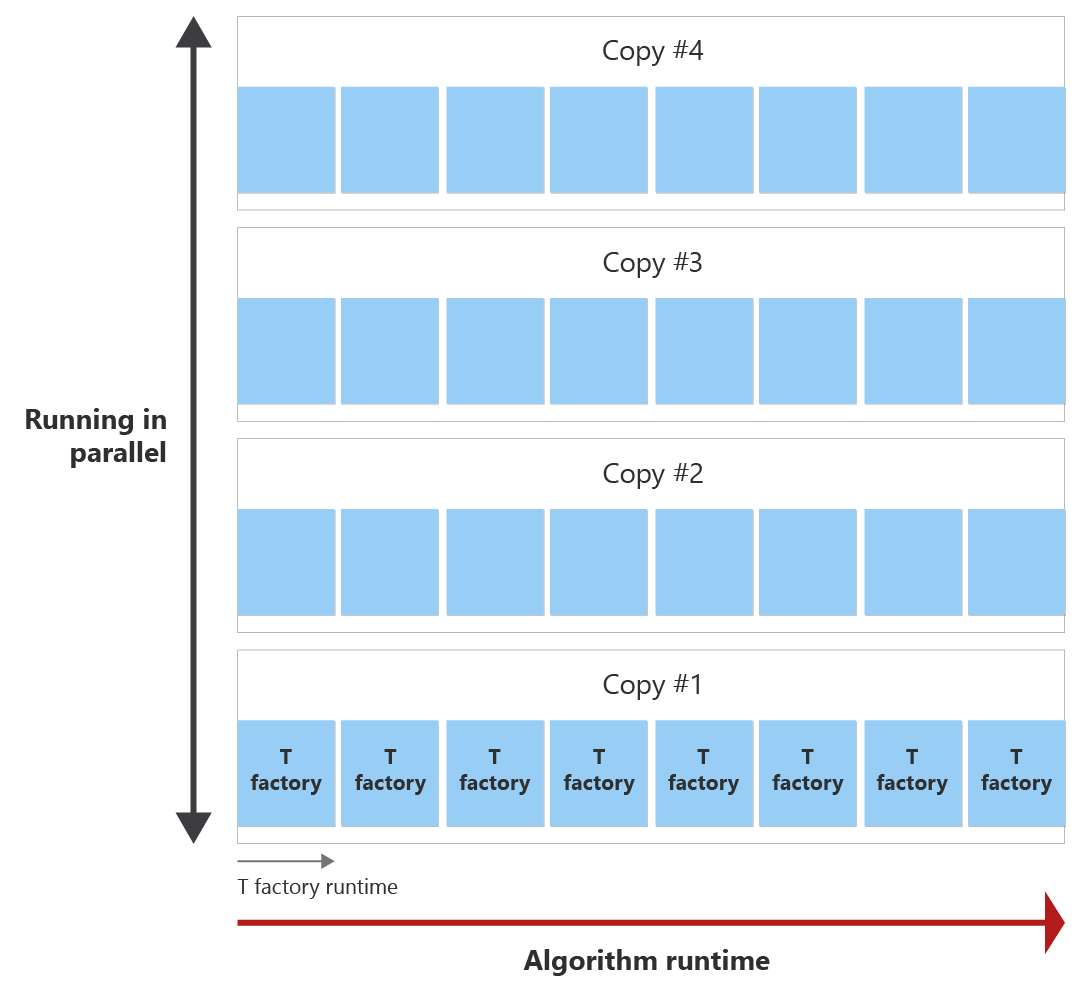
Voor het einde van het algoritme kan de T-fabriek acht keer worden aangeroepen, wat een distillatieronde wordt genoemd. Als u bijvoorbeeld 30 T-statussen nodig hebt, wordt één T-factory acht keer aangeroepen tijdens runtime van het algoritme en worden er dus acht T-statussen gemaakt. Vervolgens hebt u vier exemplaren nodig van de T factory destillatieronde parallel om de 30 T-toestanden te destilleren.
Notitie
Houd er rekening mee dat kopieën van T Factory en T Factory-aanroepen niet hetzelfde zijn.
De T-staatdestillatiefabrieken worden geïmplementeerd in een reeks rondes, waarbij elke ronde bestaat uit een reeks kopieën van distillatie-eenheden die parallel worden uitgevoerd. De resource-estimator berekent hoeveel fysieke qubits er nodig zijn om één T-factory uit te voeren en hoe lang de T-factory wordt uitgevoerd, onder andere vereiste parameters.
U kunt alleen volledige aanroepen van een T-fabriek uitvoeren. Daarom kunnen er situaties zijn waarin de geaccumuleerde runtime van alle T Factory-aanroepen kleiner is dan de algoritmeruntime. Omdat qubits opnieuw worden gebruikt door verschillende rondes, is het aantal fysieke qubits voor één T-fabriek het maximum aantal fysieke qubits dat voor één ronde wordt gebruikt. De runtime van de T-factory is de som van de runtime in alle rondes.
Notitie
Als de foutfrequentie van de fysieke T-poort lager is dan het vereiste foutpercentage van de logische T-status, kan de resource-estimator geen goede resourceraming uitvoeren. Wanneer u een resourceramingstaak verzendt, kan het voorkomen dat de T-factory niet kan worden gevonden omdat de vereiste foutpercentage van de logische T-status te laag of te hoog is.
Zie bijlage C bij het beoordelen van vereisten om te schalen naar praktisch kwantumvoordeel voor meer informatie.