Kwantumcircuitdiagramconventies

Soms zijn kwantumalgoritmen gemakkelijker te begrijpen in een circuitdiagram dan in de equivalente geschreven matrixweergave. In dit artikel wordt uitgelegd hoe u kwantumcircuitdiagrammen en hun conventies leest.

Zie Kwantumcircuitdiagrammen visualiseren voor meer informatie.

Kwantumcircuitdiagrammen lezen

In een kwantumcircuit loopt de tijd van links naar rechts. Kwantumpoorten worden in chronologische volgorde geordend met de meest linkse poort als de poort die voor het eerst op de qubits wordt toegepast.

Neem het volgende kwantumcircuitdiagram als voorbeeld:

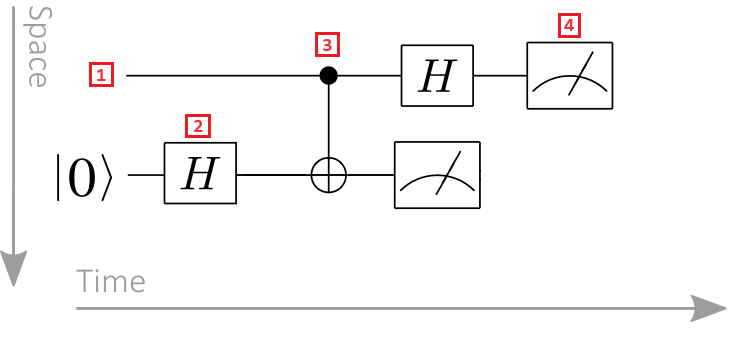
1. Qubitregister: Qubitregisters worden weergegeven als horizontale lijnen, waarbij elke regel een qubit vertegenwoordigt. De bovenste regel is qubitregister met het label 0, de tweede regel is qubitregister met het label 1, enzovoort.
2. Kwantumpoort: Kwantumbewerkingen worden vertegenwoordigd door kwantumpoorten. De term kwantumpoort is vergelijkbaar met klassieke logische poorten. Poorten die op een of meer qubitregisters reageren, worden aangeduid als een vak. In dit voorbeeld vertegenwoordigt het symbool een Hadamard-bewerking.
3. Gecontroleerde poort: Gecontroleerde poorten handelen op twee of meer qubits. In dit voorbeeld vertegenwoordigt het symbool een CNOT-poort. De zwarte cirkel vertegenwoordigt de controle-qubit en het kruis binnen een cirkel vertegenwoordigt de target qubit.
4. Meetbewerking: Het metersymbool vertegenwoordigt een meetbewerking. De metingsbewerking neemt een qubitregister op als invoer en uitvoer klassieke informatie.

Kwantumpoorten toepassen

Omdat de tijd van links naar rechts stroomt, wordt de meest linkse poort eerst toegepast. De actie van het volgende kwantumcircuit is bijvoorbeeld de eenheidsmatrix-CBA$$.

Notitie

Matrixvermendiging voldoet aan de tegenovergestelde conventie: de meest rechtse matrix wordt eerst toegepast. In kwantumcircuitdiagrammen wordt echter eerst de meest linkse poort toegepast. Dit verschil kan soms tot verwarring leiden, dus het is belangrijk om dit belangrijke verschil te noteren tussen de lineaire algebraïsche notatie en kwantumcircuitdiagrammen.

Invoer en uitvoer van kwantumcircuits

In een kwantumcircuitdiagram vertegenwoordigen de draden die een kwantumpoort invoeren de qubits die invoer voor de kwantumpoort zijn en de draden die de kwantumpoort afsluiten de qubits die van de kwantumpoort worden uitgevoerd.

Het aantal invoer van een kwantumpoort is gelijk aan het aantal uitvoer van een kwantumpoort. Dit komt doordat kwantumbewerkingen unitair zijn en daarom omkeerbaar zijn. Als een kwantumpoort meer uitvoer dan invoer had, zou deze niet omkeerbaar zijn en dus niet unitair, wat een tegenstrijdigheid is.

Om deze reden moet elk vak dat in een circuitdiagram wordt getekend precies hetzelfde aantal draden hebben dat het afsluit.

Bewerkingen met meerdere qubits

Circuitdiagrammen met meerdere qubits volgen vergelijkbare conventies als single-qubit-diagrammen. Een eenheidsbewerking $B$ met twee qubits kan bijvoorbeeld worden gedefinieerd als $(H S\otimes X),$ zodat het equivalente kwantumcircuit het volgende is:

U kunt B$ ook weergeven $als een actie op één twee-qubitregister in plaats van twee qubitregisters, afhankelijk van de context waarin het circuit wordt gebruikt.

Misschien is de handigste eigenschap van dergelijke abstracte circuitdiagrammen dat complexe kwantumalgoritmen op hoog niveau kunnen worden beschreven zonder dat ze naar fundamentele poorten hoeven te worden gecompileerd. Dit betekent dat u een intuïtieve indruk krijgt van de gegevensstroom voor een groot kwantumalgoritme zonder dat u alle details hoeft te begrijpen van hoe elk van de subroutines in het algoritme werkt.

Gecontroleerde poorten

Kwantumgestuurde poorten zijn twee qubitpoorten die een poort met één qubit toepassen op een target qubit als een controle-qubit een specifieke status heeft.

Denk bijvoorbeeld aan een kwantumgestuurde poort, aangeduid met $\Lambda(G)$, waarbij de waarde van één qubit de toepassing van de $G-bewerking$ bepaalt. De gecontroleerde poort $\Lambda(G)$ kan worden begrepen door te kijken naar het volgende voorbeeld van een productstatusinvoer:

$\Lambda(G) (\alpha\ket{{0} + \beta\ket{1}) \ket{\psi}\alpha\ket{\psi}\ket{{0}=+ G \beta\ket{{1}\ket{\psi}$

Dat wil zeggen dat de gecontroleerde poort G toepast $op het register dat $\psi$ alleen als en alleen als de controle-qubit de waarde $1$ gebruikt.$ Over het algemeen worden dergelijke gecontroleerde bewerkingen beschreven in circuitdiagrammen met het volgende symbool:

Hier geeft de zwarte cirkel de kwantumbit aan waarop de poort wordt beheerd en geeft een verticale draad de unitaire aan die wordt toegepast wanneer de controle-qubit de waarde $1$ gebruikt.

Voor de speciale gevallen waarin $G=X$ en $G=Z$ worden gebruikt, wordt de volgende notatie gebruikt om de gecontroleerde versie van de poorten te beschrijven (let op: de gecontroleerde X-poort is de CNOT-poort):

Q# biedt methoden voor het automatisch genereren van de beheerde versie van een bewerking, waardoor de programmeur deze bewerkingen niet hoeft te coden. Hieronder ziet u een voorbeeld:

operation PrepareSuperposition(qubit : Qubit) : Unit
is Ctl { // Auto-generate the controlled specialization of the operation
    H(qubit);
}

Klassieke gecontroleerde poorten

Kwantumpoorten kunnen ook worden toegepast na een meting, waarbij het resultaat van de meting fungeert als een klassieke besturingsbit.

Het volgende symbool vertegenwoordigt een klassieke gecontroleerde poort, waarbij $G$ wordt toegepast op de klassieke besturingsbit die de waarde $1$ is:

Meetoperator

Metingsbewerkingen nemen een qubitregister, meet het en voert het resultaat uit als klassieke informatie.

Een meetbewerking wordt aangeduid met een metersymbool en neemt altijd als invoer een qubitregister (aangeduid door een ononderbroken lijn) en levert klassieke informatie (aangeduid met een dubbele lijn). Het symbool van de metingsbewerking ziet er specifiek als volgt uit:

In Q#implementeert de Measure operator de meetbewerking.

Voorbeeld: Eenheidstransformatie

Overweeg de eenheidstransformatie $\text{ CNOT}_{01}(H\otimes 1)$. Deze poortreeks is van fundamenteel belang voor kwantumcomputing, omdat deze een maximaal verstrengelde twee-qubitstatus creëert:

$\mathrm{CNOT}_{01}(H\otimes 1)\left=\ket{00}\frac{1}{\sqrt{2}}({00}\ket{ + ), \ket{11}\right$

Bewerkingen met deze of grotere complexiteit zijn alomtegenwoordig in kwantumalgoritmen en kwantumfoutcorrectie.

Het circuitdiagram voor het voorbereiden van deze maximaal verstrengelde kwantumstatus is:

Het symbool achter de Hadamard-poort vertegenwoordigt een CNOT-poort, waarbij de zwarte cirkel de controle-qubit aangeeft en het kruis binnen een cirkel de target qubit aangeeft. Dit kwantumcircuit wordt weergegeven als fungerend op twee qubits (of equivalent twee registers die bestaan uit één qubit).

Voorbeeld: Diagram van teleportatiecircuit

Kwantumteleportatie is een van de beste kwantumalgoritmen voor het illustreren van circuitonderdelen.

Kwantumteleportatie is een protocol waarmee een kwantumstatus kan worden verzonden van de ene qubit naar de andere, met behulp van een gedeelde verstrengelde toestand tussen de afzender en ontvanger, en klassieke communicatie ertussen.

Voor leerdoeleinden heet de afzender Alice, wordt de ontvanger Bob genoemd en wordt de qubit die moet worden geteld, de bericht-qubit genoemd. Alice en Bob hebben één qubit en Alice heeft een extra qubit. Dit is de bericht-qubit.

Het volgende circuitdiagram illustreert het teleportatieprotocol:

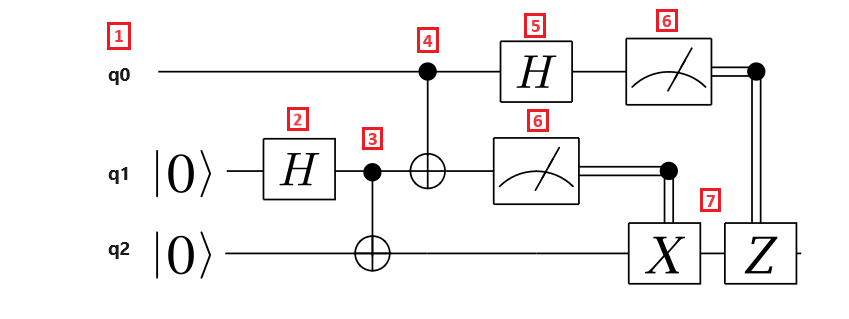
Laten we de stappen van het teleportatieprotocol opsplitsen:

1. Qubitregister q0 is de bericht-qubit, qubitregister q1 is de qubit van Alice en qubitregister q2 is de qubit van Bob. De bericht-qubit heeft een onbekende status en Alice en Bob's qubits hebben de $\ket{0}$ status.
2. Er wordt een Hadamard-poort toegepast op de qubit van Alice. Omdat de qubit de $\ket{0}$ status heeft, is $\frac{1}{\sqrt{{2}}de resulterende status (\ket{{0} + \ket{1})$.
3. Er wordt een CNOT-poort toegepast op de qubits van Alice en Bob. De qubit van Alice is de controle-qubit en de qubit van Bob is de target qubit. De resulterende status is $\frac{{1}{\sqrt{2}}(\ket{00} + \ket{{11})$. Alice en Bob delen nu een verstrengelde status.
4. Er wordt een CNOT-poort toegepast op de bericht-qubit en de qubit van Alice. Omdat de qubit van Alice ook verstrengeld is met de qubit van Bob, is de resulterende status een verstrengelde toestand van drie qubits.
5. Er wordt een Hadamard-poort toegepast op de bericht-qubit.
6. Alice meet haar twee qubits en vertelt de meetresultaten aan Bob, wat niet wordt weerspiegeld in het circuit. De meetresultaten zijn twee klassieke bits, die de waarden 00, 01, 10 of 11 kunnen aannemen.
7. Twee klassiek gecontroleerde Pauli-poorten X en Z worden toegepast op bob's qubit, afhankelijk van de resultaatbit die waarde $1$ is. De resulterende status is de oorspronkelijke qubitstatus van het bericht.

Gerelateerde inhoud

• Kwantumverstrengeling
• Algoritme van Grover
• Kwantum-tussenliggende weergave
• Vectoren en matrices