Theorie van het zoekalgoritmen van Grover
In dit artikel vindt u een gedetailleerde theoretische uitleg van de wiskundige principes die het algoritme van Grover laten werken.
Zie Het zoekalgoritmen van Grover implementeren voor een praktische implementatie van het algoritme van Grover om wiskundige problemen op te lossen.
Verklaring van het probleem
Het algoritme van Grover versnelt de oplossing tot ongestructureerde gegevenszoekopdrachten (of zoekprobleem), waarbij de zoekopdracht in minder stappen wordt uitgevoerd dan elk klassiek algoritme zou kunnen. Elke zoektaak kan worden uitgedrukt met een abstracte functie $f(x)$ die zoekitems $x$ accepteert. Als het item $x$ een oplossing is voor de zoektaak, f $(x)=1$. Als het item $x$ geen oplossing is, f $(x)=0$. Het zoekprobleem bestaat uit het vinden van een item $x_0$ zodanig dat $f(x_0)=1$.
Elk probleem waarmee u kunt controleren of een bepaalde waarde $x$ een geldige oplossing is (een " Ja of geen probleem") kan worden geformuleerd in termen van het zoekprobleem. Hier volgen enkele voorbeelden:
- Boolean satisfiability problem: Gegeven een set Booleaanse waarden, voldoet de set aan een bepaalde Booleaanse formule?
- Reizende verkoper probleem: Wat is de kortst mogelijke lus die alle steden verbindt?
- Probleem met het zoeken van databases: bevat een databasetabel de record $x$?
- Probleem met factorisatie van gehele getallen: Is het getal $N$ deelbaar door het getal $x$?
De taak die het algoritme van Grover wil oplossen, kan als volgt worden uitgedrukt: met een klassieke functie $f(x):\{0,1\}^n \rightpijl\{0,1\}$, waarbij $n$ de bitgrootte van de zoekruimte is, zoekt u een invoer $x_0$ waarvoor $f(x_0)=1$. De complexiteit van het algoritme wordt gemeten door het aantal toepassingen van de functie $f(x)$. In het ergste geval moet f(x)$ in het ergste geval $in totaal $N-1$ keer worden geëvalueerd, waarbij $N=2^n$ alle mogelijkheden uit proberen. Na $N-1$ elementen moet dit het laatste element zijn. Het kwantumalgoritmen van Grover kunnen dit probleem veel sneller oplossen, waardoor een kwadratische snelheid wordt geboden. Kwadratische hier impliceert dat alleen over $\sqrt{N}$ evaluaties vereist zou zijn, vergeleken met $N$.
Overzicht van het algoritme
Stel dat er N$2^n= in aanmerking komende items voor de zoektaak zijn $en dat ze indexeren door elk item een geheel getal van $0$ tot N-1$ toe te $wijzen. Stel dat er M verschillende geldige invoerwaarden zijn$, wat betekent dat er $M-invoer$ is waarvoor $f(x)$1=.$ De stappen van het algoritme zijn vervolgens als volgt:
- Begin met een register van $n$ qubits geïnitialiseerd in de status $\ket{0}$.
- Bereid het register voor op een uniforme superpositie door H$ toe te passen op $elke qubit van het register: $$|\text{N}\rangle=\frac{1}{\sqrt{}}_\sumx{0=^}N-1{x registreren}|\rangle$$
- Pas de volgende bewerkingen toe op het register $N_{\text{optimale}}$ aantal keren:
- Het faseorakel $O_f$ die een voorwaardelijke faseverschuiving van $-1$ toepast voor de oplossingsitems.
- $ H toepassen $op elke qubit in het register.
- Een voorwaardelijke faseverschuiving van $-1$ naar elke rekenkundige basisstatus, behalve $\ket{0}$. Dit kan worden vertegenwoordigd door de eenheidsbewerking $-O_0$, omdat $O_0$ de voorwaardelijke faseverschuiving alleen $\ket{0}$ vertegenwoordigt.
- $ H toepassen $op elke qubit in het register.
- Meet het register om de index te verkrijgen van een item dat een oplossing met zeer hoge waarschijnlijkheid is.
- Controleer of het een geldige oplossing is. Zo niet, start u opnieuw.
$N_{\text{optimale}}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{{1}{{2}\right\rfloor$ is het optimale aantal iteraties dat de kans maximaliseert om het juiste item te verkrijgen door het register te meten.
Notitie
De gezamenlijke toepassing van de stappen 3.b, 3.c en 3.d wordt meestal bekend als diffusieoperator van Grover.
De algemene eenheidsbewerking die op het register wordt toegepast, is:
$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimale}}}H^{\otimes n}$$
Stap voor stap de status van het register volgen
Laten we het proces illustreren door de wiskundige transformaties van de status van het register te volgen voor een eenvoudig geval waarin er slechts twee qubits zijn en het geldige element is $\ket{01}.$
Het register begint met de status:
$$\ket{\text{ }}=\ket{ {00}$$ registreren
Nadat $H$ op elke qubit is toegepast, verandert de toestand van het register in:
$$\ket{\text{register}}=\frac{{1}{\sqrt{4}}\sum_{i \in \lbrace 0,1 \raccolade}^2\ket{i}=\frac12(\ket{00}+\ket{01}+\ket{{10}+\ket{11})$$
Vervolgens wordt het faseorakel toegepast om het volgende te verkrijgen:
$$\ket{\text{ }} = \frac12(\ket{{00}-\ket{{01}+\ket{{10}+\ket{{11})$$
Vervolgens $H$ werkt opnieuw op elke qubit om het volgende te geven:
$$\ket{\text{registreren}}=\frac12(\ket{{00}+\ket{{01}-\ket{{10}+\ket{{11})$$
De voorwaardelijke faseverschuiving wordt nu toegepast op elke status behalve $\ket{00}$:
$$\ket{\text{ }} = \frac12(\ket{{00}-\ket{{01}+\ket{{10}-\ket{{11})$$
Ten slotte eindigt de eerste Grover-iteratie door $H-$ opnieuw toe te passen om het volgende te krijgen:
$$\ket{\text{ }} = \ket{ {01}$$ registreren
Door de bovenstaande stappen te volgen, wordt het geldige item in één iteratie gevonden. Zoals u later zult zien, is dit omdat voor N=4 en één geldig item het optimale aantal keren dat $N_{\text{optimaal}}=1$.
Geometrische uitleg
Om te zien waarom het algoritme van Grover werkt, gaan we het algoritme bestuderen vanuit een geometrisch perspectief. Stel dat er $M$ geldige oplossingen zijn, de superpositie van alle kwantumtoestanden dat geen oplossing voor het zoekprobleem:
$$\ket{\text{bad}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$
De superpositie van alle toestanden die een oplossing zijn voor het zoekprobleem:
$$\ket{\text{goede}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$
Omdat goede en slechte elkaar uitsluiten omdat een item niet geldig en ongeldig kan zijn, zijn de statussen orthogonaal. Beide toestanden vormen de orthogonale basis van een vlak in de vectorruimte. U kunt dit vlak gebruiken om het algoritme te visualiseren.
Stel dat $\ket{\psi}$ het een willekeurige toestand is die zich in het vliegtuig bevindt dat goed $\ket{\text{}}$ en $\ket{\text{slecht}}$ is. Elke toestand die in dat vliegtuig woont, kan worden uitgedrukt als:
$$\ket{\psi} = \alpha \ket{\text{goed}} + \beta\ket{\text{slecht}}$$
waar $\alpha$ en $\beta$ zijn reële getallen. Laten we nu de weerspiegelingsoperator $introduceren R_{\ket{\psi}}$, waar $\ket{\psi}$ zich een qubitstatus bevindt die in het vliegtuig woont. De operator is gedefinieerd als:
$$ {\ket{\psi}}=R_2\ket{\psi}\bra{\psi}-\mathcal{I}$$
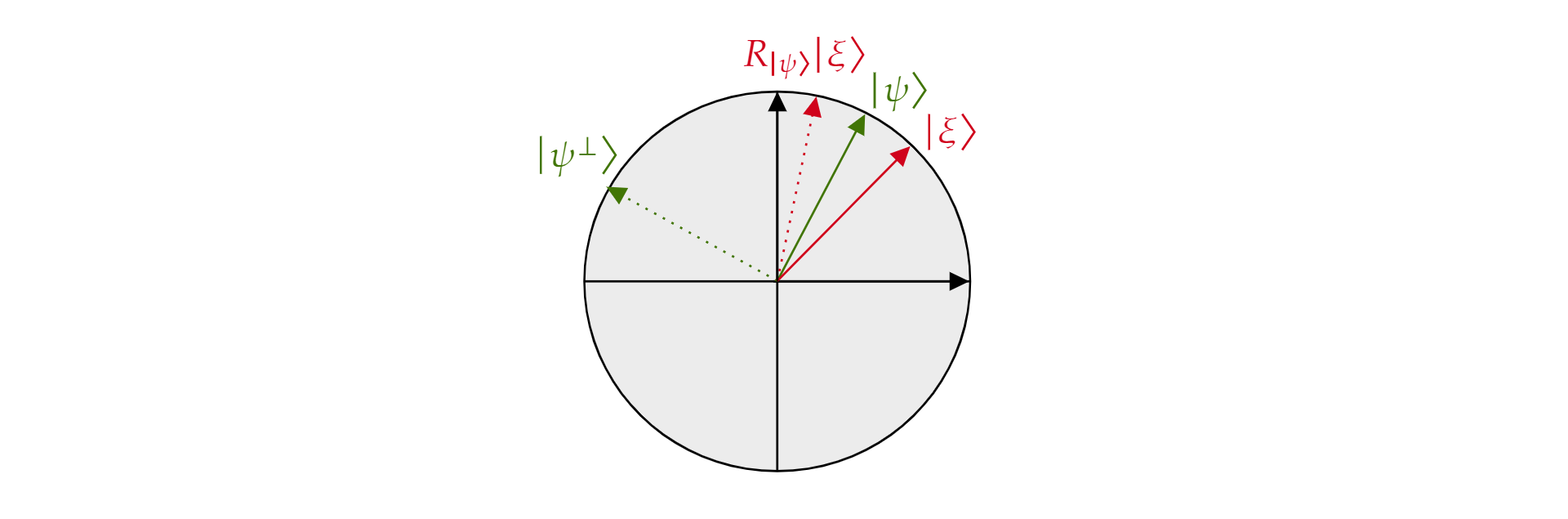
Het wordt de weerspiegelingsoperator $\ket{\psi}$ genoemd omdat het geometrisch kan worden geïnterpreteerd als reflectie over de richting van $\ket{\psi}$. Om het te zien, neemt u de orthogonale basis van het vlak gevormd door $\ket{\psi}$ en de orthogonale complement $\ket{\psi^{\perp}}$. Elke toestand $\ket{\xi}$ van het vliegtuig kan in een dergelijke basis worden gedecomposeerd:
$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$
Als de operator $R_{\ket{\psi}}$ wordt toegepast op $\ket{\xi}$:
$$ {\ket{\psi}}\ket{R_\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$
De operator $R_{\ket{\psi}}$ het onderdeel orthogonaal omkeren, $\ket{\psi}$ maar het onderdeel blijft $\ket{\psi}$ ongewijzigd. $Daarom is R_{\ket{\psi}}$ een reflectie over $\ket{\psi}$.
Het algoritme van Grover, na de eerste toepassing van $H$ op elke qubit, begint met een uniforme superpositie van alle toestanden. Dit kan worden geschreven als:
$$\ket{\text{alle}}=\sqrt{\frac{M}{N}}\ket{\text{goed}} + \sqrt{\frac{N-M}{N}}\ket{\text{slecht}}$$
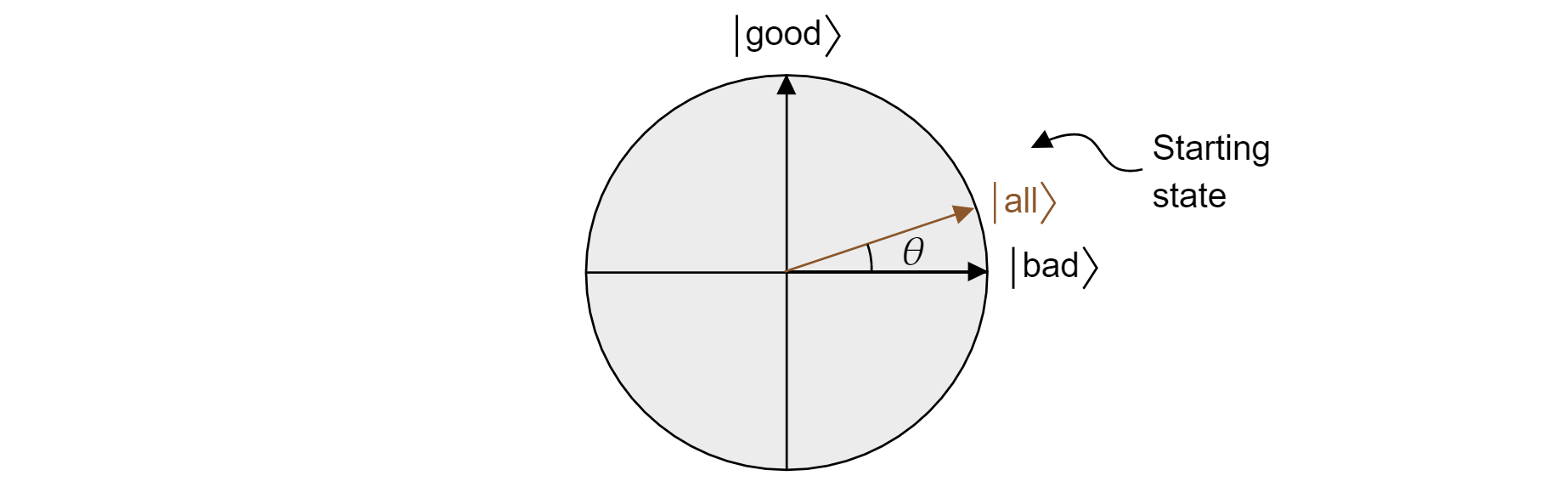
En zo leeft de staat in het vliegtuig. Houd er rekening mee dat de kans op het verkrijgen van een correct resultaat bij het meten van de gelijke superpositie alleen $|\bra{\text{goed}}\ket{\text{is voor alle}}|^2=M/N$, wat u zou verwachten van een willekeurige schatting.
Het oracle $O_f$ voegt een negatieve fase toe aan elke oplossing voor het zoekprobleem. Daarom kan het worden geschreven als reflectie over de $\ket{\text{slechte}}$ as:
$$O_f = R_{\ket{\text{slechte}}}= 2\ket{\text{slechte}}\bra{\text{slechte}} - \mathbb{I}$$
Analoog is de voorwaardelijke fase shift $O_0$ slechts een omgekeerde reflectie over de toestand $\ket{0}$:
$$O_{0}= R_{\ket{0}}= -2\ket{{0}\bra{{0} + \mathbb{I}$$
Als u dit weet, is het gemakkelijk om te controleren of de Grover-diffusiebewerking $-H^{\otimes n} O_{0} H^{\otimes n}$ ook een reflectie is over de staat $\ket{alle}$. Doe het gewoon:
$$-H^{\otimes n} O_{{0} H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{{0}H^{\otimes n} -H^{\otimes n}\mathbb{I}H^{\otimes n}= 2\ket{\text{alle}}\bra{\text{alle}} - \mathbb{I}= R_{\ket{\text{alle}}}$$
Er is aangetoond dat elke iteratie van het algoritme van Grover een samenstelling is van twee reflecties $R_{\ket{\text{bad}}}$ en $R_{\ket{\text{all}}}$.
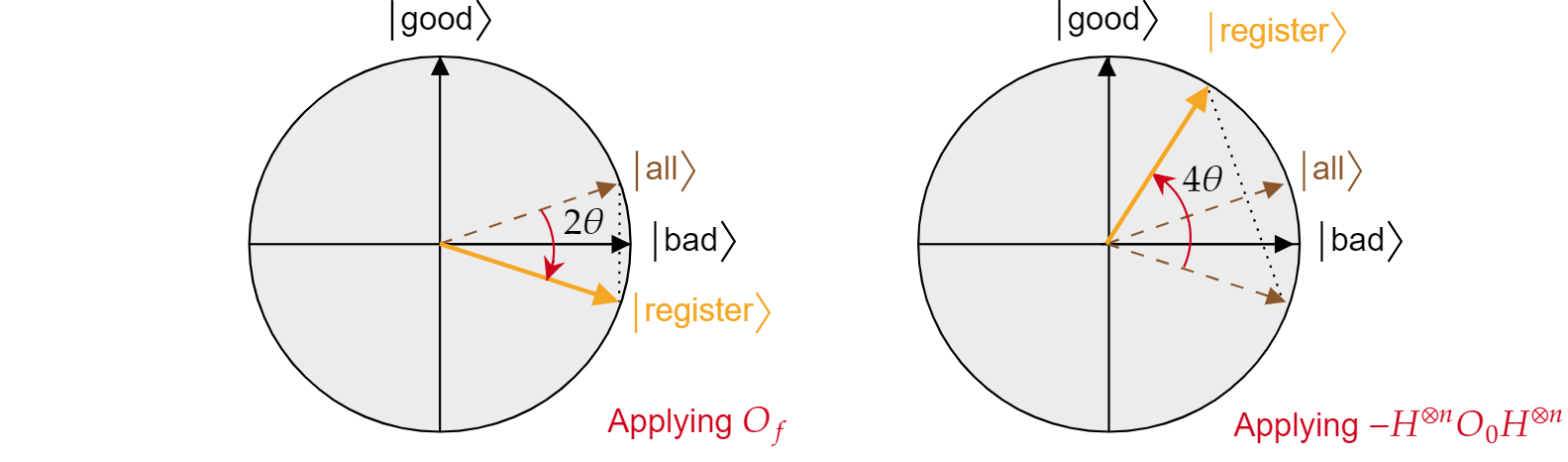
Het gecombineerde effect van elke Grover-iteratie is een tegenklokgewijze draaiing van een hoek $2\theta$. Gelukkig is de hoek $\theta$ gemakkelijk te vinden. Omdat $\theta$ slechts de hoek is tussen $\ket{\text{alles}}$ en $\ket{\text{slecht}}$, kan men het scalaire product gebruiken om de hoek te vinden. Het is bekend dat $\cos{\theta}=\braket{\text{allemaal}|\text{slecht}}$, dus één moet alle$\braket{\text{slechte}|\text{ berekenen}}$. Uit de ontleding van $\ket{\text{alles}}$ in termen van $\ket{\text{slecht}}$ en $\ket{\text{goed}}$, volgt het:
$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$
De hoek tussen de toestand van het register en de $\ket{\text{goede}}$ toestand neemt af bij elke iteratie, wat resulteert in een hogere kans op het meten van een geldig resultaat. Als u deze waarschijnlijkheid wilt berekenen, hoeft u alleen een goed register^2$|\braket{\text{ te berekenen}|\text{.}}|$ De hoek tussen $\ket{\text{good}}$ en $\ket{\text{register}}$ wordt aangeduid als $\gamma (k)$, waarbij $k$ de iteratietelling is:
$$\gamma = \frac{\pi}{2}-\theta -2k\theta =\frac{\pi}{{2} -(2k + 1) \theta $$
Daarom is de kans op succes:
$$P(\text{geslaagd}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$
Optimaal aantal iteraties
Aangezien de kans op succes kan worden geschreven als een functie van het aantal iteraties, kan het optimale aantal iteraties $N_{\text{optimaal}}$ worden gevonden door het kleinste positieve gehele getal te berekenen dat (ongeveer) de kans op succes maximaliseert.
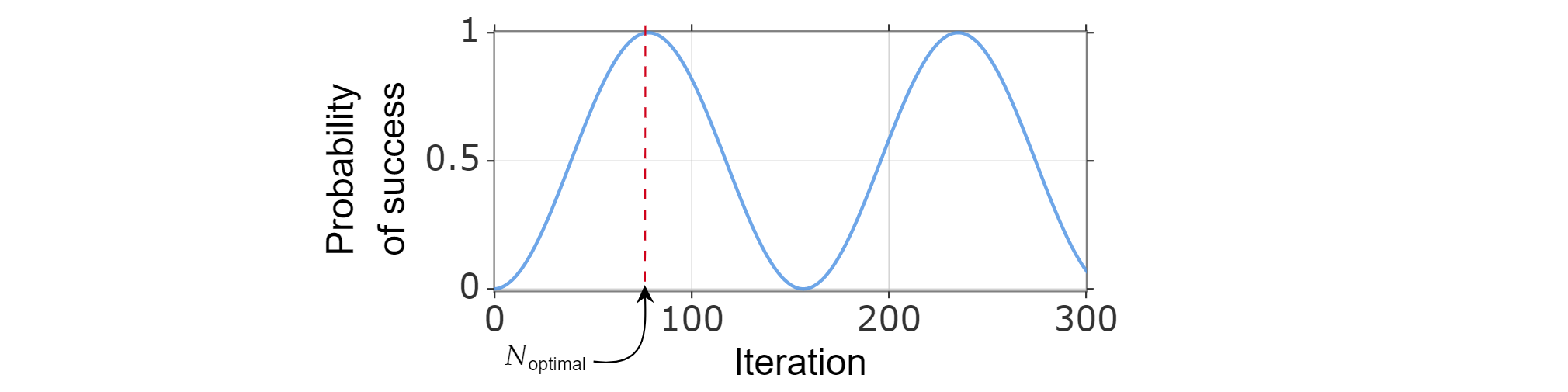
Het is bekend dat $\sin^2{x}$ het eerste maximum voor $x=\frac{\pi}{2}$ bereikt, dus:
$$\frac{\pi}{{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$
Dit geeft het volgende:
$$ {\text{k_optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 =\frac{\pi}{{4}\sqrt{\frac{N}{M-O}}\frac{1}{2}\left(\sqrt\frac{M}{N)}\right$$
Waar in de laatste stap\arccos 1-x$\sqrt{}= + O(x^\sqrt{3/2}).{}$
Daarom kunt u $N_{\text{optimale}}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{{1}{{2}\right\rvloer$kiezen.
Complexiteitsanalyse
Uit de vorige analyse $zijn O\left(\sqrt{\frac{N}{M}}\right)$ -query's van het oracle $O_f$ nodig om een geldig item te vinden. Kan het algoritme echter efficiënt worden geïmplementeerd in termen van tijdcomplexiteit? $ $ O_0 is gebaseerd op het berekenen van Booleaanse bewerkingen op $n$ bits en is bekend dat deze kan worden geïmplementeerd met behulp van $O(n)$ gates. Er zijn ook twee lagen van $n$ Hadamard-poorten. Beide onderdelen vereisen dus slechts $O(n)$ poorten per iteratie. Omdat $N=2^n$ volgt, volgt dit O $(n)=O(log(N))$. Als O($N\leftM\sqrt{\frac{)}{-iteraties en }}\rightO(log(N)-$poorten per iteratie nodig zijn, is $de totale tijdcomplexiteit (zonder rekening te houden met de oracle-implementatie) O$($N\leftM\sqrt{\frac{log(N)))}{.}}\right$
De algehele complexiteit van het algoritme is uiteindelijk afhankelijk van de complexiteit van de implementatie van het oracle $O_f$. Als een functie-evaluatie veel ingewikkelder is op een kwantumcomputer dan op een klassieke computer, is de algehele algoritmeruntime langer in het kwantumscenario, ook al worden er technisch gezien minder query's gebruikt.
Verwijzingen
Als u meer wilt weten over het algoritme van Grover, kunt u een van de volgende bronnen controleren:
- Originele krant van Lov K. Grover
- Sectie kwantumzoekalgoritmen van De sectie Van Den 1244, M. A. &Amp; Chuang, I. L. (2010). Kwantumberekening en kwantuminformatie.
- Het algoritme van Grover op Arxiv.org