D3DXSHEvalHemisphereLight-Funktion (D3dx9math.h)

Hinweis

Die Hilfsprogrammbibliothek D3DX (D3DX 9, D3DX 10 und D3DX 11) ist veraltet und wird für Windows Store-Apps nicht unterstützt.

Hinweis

Anstatt diese Funktion zu verwenden, empfiehlt es sich, die Bibliotheksfunktion Spherical Harmonics MathXMSHEvalHemisphereLight zu verwenden.

Wertet ein Licht aus, bei dem es sich um eine lineare Interpolation zwischen zwei Farben über der Kugel handelt.

Syntax

HRESULT D3DXSHEvalHemisphereLight(
  _In_       UINT        Order,
  _In_ const D3DXVECTOR3 *pDir,
  _In_       D3DXCOLOR   Top,
  _In_       D3DXCOLOR   Bottom,
  _In_       FLOAT       *pROut,
  _In_       FLOAT       *pGOut,
  _In_       FLOAT       *pBOut
);

Parameter

Reihenfolge [in]

Typ: UINT

Reihenfolge der sphärisch harmonischen (SH)-Auswertung. Muss im Bereich der D3DXSH_MINORDER liegen, um D3DXSH_MAXORDER inklusive. Die Auswertung generiert Order²-Koeffizienten. Der Grad der Auswertung ist Order - 1.

pDir [in]

Typ: const D3DXVECTOR3*

Zeiger auf den (x, y, z) Hemisphärenachsenrichtungsvektor, in dem die SH-Basisfunktionen ausgewertet werden sollen. Siehe Hinweise.

Oben [in]

Typ: D3DXCOLOR

Die Himmelsfarbe.

Unten [in]

Typ: D3DXCOLOR

Die Grundfarbe.

pROut [in]

Typ: FLOAT*

Zeiger auf den SH-Ausgabevektor für die rote Komponente.

pGOut [in]

Typ: FLOAT*

Zeiger auf den SH-Ausgabevektor für die grüne Komponente.

pBOut [in]

Typ: FLOAT*

Zeiger auf den SH-Ausgabevektor für die blaue Komponente.

Rückgabewert

Typ: HRESULT

Wenn die Funktion erfolgreich ist, wird der Rückgabewert D3D_OK. Wenn die Funktion fehlschlägt, kann der Rückgabewert sein: D3DERR_INVALIDCALL.

Bemerkungen

Die Interpolation erfolgt linear zwischen den beiden Punkten, nicht über der Oberfläche der Kugel (das heißt, wenn die Achse (0,0,1) war, ist sie in Z linear, nicht im azimuthalalen Winkel). Die resultierende sphärische Beleuchtungsfunktion wird so normalisiert, dass ein Punkt auf einer perfekt diffusen Oberfläche ohne Schatten und ein normaler Punkt in Richtung pDir zu einer Exitstrahlung mit einem Wert von 1 führen würde (wenn die obere Farbe weiß und die untere Farbe schwarz war). Dies ist ein sehr einfaches Modell, bei dem Top die Intensität des "Himmels" und Bottom die Intensität des "Bodens" darstellt.

Auf der Kugel mit Einheitsradius, wie in der folgenden Abbildung dargestellt, kann die Richtung einfach mit Theta, dem Winkel um die Z-Achse in rechtshändiger Richtung und phi, dem Winkel von z, angegeben werden.

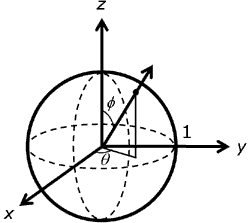
Die folgenden Formeln zeigen die Beziehung zwischen kartesischen (x, y, z) und kugelförmigen Koordinaten (Theta, phi) auf der Einheitskugel. Der Winkel theta variiert im Bereich von 0 bis 2 Pi, während phi von 0 bis pi variiert.

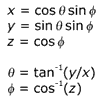
Anforderungen

Anforderung	Wert
Header	D3dx9math.h
Bibliothek	D3dx9.lib

Siehe auch

Mathematische Funktionen

Vorberechnete Radianzübertragung (Direct3D 9)