Das Qubit im Quantencomputing
Genau wie Bits das grundlegende Informationsobjekt beim klassischen Computing sind, sind Qubits (Quantenbits) das grundlegende Objekt von Informationen im Quantencomputing. Um diese Korrespondenz zu verstehen, betrachtet dieser Artikel das einfachste Beispiel: ein einzelnes Qubit.
Darstellen eines Qubits
Während ein Bit bzw. eine binäre Ziffer entweder den Wert $0$ oder $1$ haben kann, kann ein Qubit einen Wert haben, der entweder $0$, $1$ oder eine Quantenüberlagerung von $0$ und $1$ ist.
Der Zustand eines einzelnen Qubits kann durch einen zweidimensionalen Spaltenvektor der Einheitennorm beschrieben werden, d. h., die Größe im Quadrat der Einträge muss mit $ 1$ summiert werden. Dieser Vektor, der sogenannte Quantenzustandsvektor, enthält alle Informationen, die zur Beschreibung des Ein-Qubit-Quantensystems benötigt werden, so wie ein einzelnes Bit alle Informationen enthält, die zur Beschreibung des Zustands einer binären Variablen benötigt werden. Die Grundlagen von Vektoren und Matrizen in der Quantenberechnung finden Sie unter Vector und Matrizen.
Jeder zweidimensionale Spaltenvektor aus reellen oder komplexen Zahlen mit der Norm $1$ repräsentiert einen möglichen Quantenzustand, der von einem Qubit gehalten wird. Stellt daher $\begin{bmatrix} \alpha \\ \beta \end{bmatrix}$ einen Qubitzustand dar, wenn $\alpha$ und $\beta$ komplexe Zahlen sind, die $|\alpha|^2 + |\beta|^2 = 1 $ erfüllen. Einige Beispiele für gültige Quantenzustandsvektoren, die Qubits darstellen, sind
$$\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \end{bmatrix}, \begin{bmatrix}\frac{{1}{\sqrt{2}}\\\frac{{1}{\sqrt{2}}\end{bmatrix}, \begin{bmatrix}\frac{1}{\sqrt{{2}}\\\frac{{-1}{\sqrt{2}}\end{bmatrix}, \text{ und }\begin{bmatrix}\frac{1}{\sqrt{{2}}\\\frac{i}{\sqrt{2}}\end{bmatrix}.$$
Die Quantenzustandsvektoren $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ und $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ nehmen eine besondere Rolle ein. Diese beiden Vektoren bilden eine Basis für den Vektorraum, der den Zustand des Qubits beschreibt. Das bedeutet, dass jeder Quantenzustandsvektor als eine Summe dieser Basisvektoren geschrieben werden kann. Insbesondere kann der Vektor $\begin{bmatrix} x \\ y \end{bmatrix}$ als $x \begin{bmatrix} 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix}$ geschrieben werden. Zwar könnte jede Rotation dieser Vektoren als absolut gültige Basis für das Qubit dienen, aber hier wird die obige Wahl getroffen und als Berechnungsbasis bezeichnet.
Diese beiden Quantenzustände werden als Entsprechung der beiden Zustände eines klassischen Bits verwendet, nämlich $0$ und $1$. Die Standardkonvention ist die Auswahl von
$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \qquad 1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix},$$
wobei die umgekehrte Wahl genauso gut getroffen werden könnte. So entsprechen von der unendlichen Anzahl möglicher Ein-Qubit-Quantenzustandsvektoren nur zwei den Zuständen klassischer Bits, alle anderen Quantenzustände nicht.
Messen eines Qubits
Nachdem die Darstellung eines Qubits beschrieben wurde, können wir unsere Fähigkeiten ausbauen, um intuitiv besser erkennen zu können, was diese Zustände repräsentieren. Hierzu wird das Konzept der Messung beschrieben. Eine Messung entspricht der informellen Vorstellung des „Hinschauens“ auf ein Qubit, wodurch der Quantenzustand sofort auf einen der beiden klassischen Zustände kollabiert $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ oder $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Wenn ein vom Quantenzustandsvektor angegebenes Qubit $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ gemessen wird, führt dies zum Ergebnis $0$ mit der Wahrscheinlichkeit $|\alpha|^2$ und dem Ergebnis $1$ mit der Wahrscheinlichkeit $|\beta|^2$. Zum Ergebnis $0$, der neue Zustand des Qubits ist $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$; im Ergebnis $1$ sein Zustand ist $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Beachten Sie, dass diese Wahrscheinlichkeiten sich $1$ aufgrund der Normalisierungsbedingung $|\alpha|^2 + |\beta|^2 = bis zu 1 summieren$.
Die Eigenschaften der Messung bedeuten auch, dass das Gesamtzeichen des Quantenzustandsvektors irrelevant ist. Das Negieren eines Vektors entspricht $\alpha \rightPfeil -\alpha$ und $\beta\rightPfeil -\beta$. Da die Wahrscheinlichkeit der Messung von $ 0 $ und $ 1 $ von der Quadratgröße der Begriffe abhängt, ändert das Einfügen solcher Zeichen die Wahrscheinlichkeiten nicht. Solche Phasen werden häufig als &„globale Phasen“& bezeichnet und können im Allgemeinen das Format $e^{i \phi}$ und nicht nur $\pm 1$ haben.
Eine letzte wichtige Eigenschaft der Messung ist, dass sie nicht unbedingt alle Quantenzustandsvektoren beschädigt. Wenn mit einem Qubit im Zustand $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ begonnen wird, was dem klassischen Zustand $0$ entspricht, ergibt die Messung dieses Zustands immer das Ergebnis $0$, und der Quantenzustand bleibt unverändert. Wenn wir in diesem Sinne nur über klassische Bits verfügen (z. B. Qubits, die entweder $\begin{bmatrix}1 \\ 0 \end{bmatrix}$ oder $\begin{bmatrix}0 \\ 1 \end{bmatrix}$ sind), beschädigt die Messung das System nicht. Dies bedeutet, dass klassische Daten repliziert und auf einem Quantencomputer genauso manipuliert werden können, wie dies auf einem klassischen Computer möglich wäre. Die Fähigkeit, Informationen in beiden Zuständen gleichzeitig zu speichern, ist jedoch das, was das Quantencomputing über das hinaushebt, was klassisch möglich ist, und was Quantencomputern außerdem die Fähigkeit nimmt, Quantendaten wahllos zu kopieren, siehe auch das No-Cloning-Theorem.
Visualisieren von Qubits und Transformationen mithilfe der Bloch-Kugel
Qubits können auch in $3$D mit der Bloch-Kugel-Darstellung abgebildet werden. Die Bloch-Kugel bietet eine Möglichkeit, einen Ein-Qubit-Quantenzustand (der ein zweidimensionaler komplexer Vektor ist) als dreidimensionalen reellwertigen Vektor zu beschreiben. Dies ist wichtig, weil es uns erlaubt, Ein-Qubit-Zustände zu visualisieren und dadurch Schlussfolgerungen zu entwickeln, die für das Verständnis von Multi-QuBit-Zuständen von unschätzbarem Wert sein können (wo leider die Bloch-Kugel-Darstellung zusammenbricht). Die Bloch-Kugel kann wie folgt visualisiert werden:
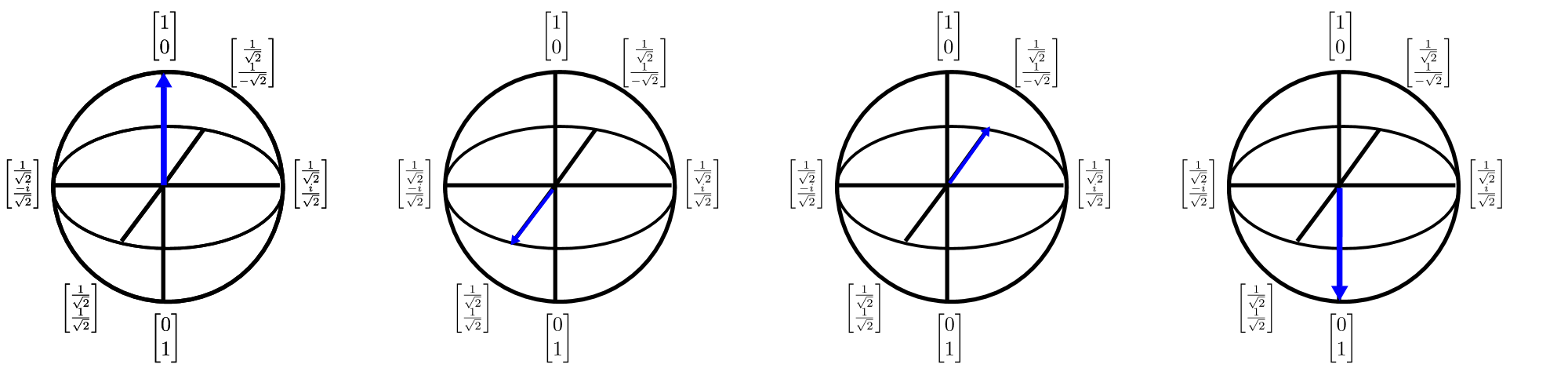
Die Pfeile in diesem Diagramm zeigen die Richtung an, in die der Quantenzustandsvektor zeigt, und jede Transformation des Pfeils kann als eine Drehung um eine der Kardinalachsen gedacht werden. Während die Vorstellung einer Quantenberechnung als eine Folge von Rotationen eine mächtige Intuition ist, ist es eine Herausforderung, diese Intuition zu nutzen, um Algorithmen zu entwerfen und zu beschreiben. Q# entschärft dieses Problem, indem es eine Sprache zur Beschreibung solcher Rotationen bereitstellt.
Ein-Qubit-Operationen
Quantencomputer verarbeiten Daten durch Anwendung eines universellen Satzes von Quanten-Gates, die eine beliebige Rotation des Quantenzustandsvektors emulieren können. Dieser Begriff der Universalität ist verwandt mit dem Begriff der Universalität für traditionelles (z. B. klassisches) Rechnen, bei dem eine Gate-Menge als universell angesehen wird, wenn jede Transformation der Eingangsbits mit einer Schaltung endlicher Länge durchgeführt werden kann. Im Quantencomputing sind die gültigen Transformationen, die wir auf einem Qubit durchführen dürfen, Einheitstransformationen und Messungen. Der Adjunkten-Vorgang oder die komplex-konjugierte Transponierung ist für das Quantencomputing von entscheidender Bedeutung, da sie zur Invertierung von Quantentransformationen benötigt wird.
Single-Qubit-Operationen oder Single-Qubit-Quantentore können in zwei Kategorien unterteilt werden: Clifford-Tore und die Nicht-Clifford-Tore. Nicht-Clifford-Tore bestehen nur $aus T-Gate$ (auch bekannt als $\pi/8$ Gate).
$$T=\begin{bmatrix} 1 amp; 0 0 &\\ amp; e^{i\pi/4\end{bmatrix}}.& $$
Der Standardsatz von Single-Qubit Clifford-Toren, standardmäßig enthalten in Q#, enthalten
$$H=\frac{{2}}\begin{bmatrix}{1}{\sqrt{ 1 & 1 1 \\ &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 0 \\ & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 1 \\& 0 \end{bmatrix}= HT^4H,$$
$$Y =0 amp; -i i &\\ amp; 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1&&\begin{bmatrix} 0 0\\& amp;-1 \end{bmatrix}=T^4. $$
Hier werden die Vorgänge $X$, $Y$ und $Z$ besonders häufig verwendet und werden nach ihrem Ersteller Wolfgang Pauli genannt. Zusammen mit dem Non-Clifford-Gate ($T$-Gate) können diese Vorgänge zusammengesetzt werden, um eine ungefähre Einheitstransformation für ein einzelnes Qubit zu erreichen.
Während die vorhergehenden die populärsten primitiven Gates zur Beschreibung von Operationen auf der logischen Ebene des Stacks darstellen (denken Sie an die logische Ebene als die Ebene des Quantenalgorithmus), ist es oft bequem, weniger grundlegende Operationen auf der algorithmischen Ebene zu betrachten, zum Beispiel Operationen, die näher an einer Funktionsbeschreibungsebene liegen. Glücklicherweise Q# stehen auch Methoden zum Implementieren von Einheiten auf höherer Ebene zur Verfügung, die wiederum die Implementierung von Algorithmen auf hoher Ebene ermöglichen, ohne dass alles explizit auf Dietord und $T$-Gates zerlegt wird.
Das einfachste solche Primitiv ist die Einzel-Qubit-Rotation. In der Regel werden drei Single-Qubit-Drehungen berücksichtigt: $R_x$, $R_y$ und $R_z$. Um die Aktion der Drehung $R_x(\theta)$, zu visualisieren, stellen Sie sich beispielsweise vor, dass Sie ihren rechten Daumen auf die Richtung der $x$-Achse der Bloch-Kugel zeigen und den Vektor mit der Hand durch einen Winkel von $\theta/2$Bogenmaß drehen. Dieser verwirrende Faktor von $2$ ergibt sich aus der Tatsache, dass orthogonale Vektoren $180^\circ$ auseinander liegen, wenn sie auf der Bloch-Kugel gezeichnet werden, aber tatsächlich $90^\circ$-Grad geometrisch voneinander entfernt sind. Die entsprechenden Einheitsmatrizen sind:
\begin{ausrichten*}& R_z(\theta) = e^{-i\theta Z/2}=\begin{bmatrix} e^{-i\theta/2&}amp; 0 0\\& amp; e^{i\theta/2\end{bmatrix}}, \\& R_x(\theta) e^{-i\theta X/2=} HR_z(\theta)H =\begin{bmatrix} \cos(\theta/2) & -i\sin(\theta/2)\\ -i\sin(\theta/2) & \cos(\theta/2) \end{bmatrix}, \\& = R_y(\theta) e^-i\theta Y/2}= SHR_z(\theta)HS^\begin{bmatrix}=\dagger \cos(\theta/2) & -\sin(\theta/2)\\ \sin(\theta/2) & \cos(\theta/2) \end{bmatrix}.{= \end{align*}
Genauso wie drei beliebige Drehungen miteinander kombiniert werden können, um eine beliebige Drehung in drei Dimensionen durchzuführen, kann aus der Bloch-Kugel-Darstellung ersehen werden, dass jede Einheitsmatrix auch als eine Folge von drei Drehungen geschrieben werden kann. Speziell für jede Einheitsmatrix $U$ gibt es dort $\alpha\beta,\gamma,\delta$ wie z.B $U= e^{i\alpha} R_x(\beta)R_z(\gamma)R_x(\delta)$. Somit bilden$R_z(\theta)$ und $H$ ebenfalls eine universelle Gate-Menge, obwohl es sich nicht um eine diskrete Menge handelt, da $\theta$ jeden Wert annehmen kann. Aus diesem Grund und aufgrund von Anwendungen in der Quantensimulation sind solche kontinuierlichen Gates entscheidend für die Quantenberechnung, insbesondere auf der Ebene des Entwurfs von Quantenalgorithmen. Um eine fehlertolerante Hardware-Implementierung zu erreichen, werden sie schließlich in diskrete Gate-Sequenzen kompiliert, die sich diesen Rotationen stark annähern.