Die Rolle von T Gates und T-Fabriken im Quanten computing
In diesem Artikel wird die Rolle von T Gates und T-Fabriken in fehlertoleranten Quantencomputern beschrieben. Angesichts eines Quantenalgorithmus wird die Schätzung der erforderlichen Ressourcen für die Ausführung der T-Tore und T-Fabriken entscheidend, um die Machbarkeit des Algorithmus zu bestimmen. Der Azure Quantum Resource Estimator berechnet die Anzahl der T-Zustände, die zum Ausführen des Algorithmus erforderlich sind, die Anzahl der physischen Qubits für eine einzelne T-Factory und die Laufzeit der T-Factory.
Universelle Gruppe von Quantentoren
Nach diVincenzos Kriterien muss ein skalierbarer Quantencomputer in der Lage sein, einen universellen Satz von Quantentoren zu implementieren. Ein universeller Satz enthält alle Tore, die zum Ausführen einer Quantenberechnung erforderlich sind, d. h., jede Berechnung muss in eine endliche Abfolge universeller Tore zurückkompiliert werden. Mindestens muss ein Quantencomputer einzelne Qubits an eine beliebige Position auf der Bloch-Kugel (mit Single-Qubit-Toren) verschieben und eine Verangle im System einführen, die ein Multi-Qubit-Gate erfordert.
Auf einem klassischen Computer gibt es nur vier Funktionen, die ein Bit auf ein Bit abbilden. Im Gegensatz dazu gibt es auf einem einzelnen Qubit eines Quantencomputers unendlich viele Einheitstransformationen. Daher kann kein endlicher Satz von primitiven Quantenvorgängen oder Toren genau den unendlichen Satz von Einheitentransformationen replizieren, die in der Quantenberechnung zulässig sind. Das heißt, im Gegensatz zum klassischen Rechnen ist es für einen Quantencomputer unmöglich, jedes mögliche Quantenprogramm mit einer endlichen Anzahl von Gates exakt zu implementieren. Daher können Quantencomputer nicht im gleichen Sinne universell sein wie klassische Computer. Wenn wir also sagen, dass eine Reihe von Gates für Quantencomputing universell ist, meinen wir tatsächlich etwas schwächer als beim klassischen Computing.
Für die Universalität ist es erforderlich, dass ein Quantencomputer nur jede Einheitsmatrix innerhalb eines endlichen Fehlers annähert, wobei eine endliche Gatesequenz verwendet wird.
Mit anderen Worten, eine Menge von Gates ist eine universelle Gate-Menge, wenn jede Einheitstransformation näherungsweise als ein Produkt von Gates aus dieser Menge geschrieben werden kann. Es ist erforderlich, dass für jede vorgeschriebene Fehlerbindung Tore $G_{1}, G_{2}, \ldots, G_N$ vom Gate festgelegt sind, so dass
$$ G_N G_{N-1}\cdots G_2 G_1 \approx U. $$
Da die Konvention für die Matrixmultiplikation darin besteht, den ersten Gate-Vorgang in dieser Sequenz von rechts nach links zu multiplizieren, $ist G_N$ tatsächlich der letzte, der auf den Quantenzustandsvektor angewendet wird. Formaler ausgedrückt wird eine Gate-Menge dieser Art als universell bezeichnet, wenn für jede Fehlertoleranz \$\epsilon>0$ $G_1,\ldots, G_N$ vorhanden ist, sodass der Abstand zwischen $G_N\ldots G_1$ und $U$ maximal $ \epsilon$ ist. Idealerweise sollte der Wert von $N$, der benötigt wird, um diesen Abstand von $\epsilon$ zu erreichen, polylogarithmisch mit $1/\epsilon$ skalieren.
Beispielsweise ist der satz, der von Hadamard, CNOT und T Gates gebildet wird, ein universeller Satz, aus dem jede Quantenberechnung (auf einer beliebigen Anzahl von Qubits) generiert werden kann. Der Hadamard- und der T-Gate-Satz generiert jedes Single-Qubit-Gate:
$$H=\frac{1}{\sqrt{ 1 amp; 1 1 \\ &-1 \end{bmatrix}, \qquad T=\begin{bmatrix} 1 & 0 0 \\ & e^{i\pi/4.\end{bmatrix}}&{2}}\begin{bmatrix} $$
In einem Quantencomputer können Quantentore in zwei Kategorien unterteilt werden: Clifford-Tore und Nicht-Clifford-Tore, in diesem Fall das T-Tor. Quantenprogramme, die nur von Clifford-Toren hergestellt werden, können effizient mit einem klassischen Computer simuliert werden, und daher sind nicht-Clifford-Tore erforderlich, um Quantenvorteile zu erhalten. In vielen QEC-Schemas (Quantum Error Correction) sind die sogenannten Clifford Gates einfach zu implementieren, d. h., sie erfordern sehr wenige Ressourcen in Bezug auf Vorgänge und Qubits, um fehlertolerant zu implementieren, während Nicht-Clifford-Tore recht kostspielig sind, wenn fehlertoleranz erforderlich ist. In einem universellen Quantentorsatz wird das T-Tor häufig als nicht-Clifford-Tor verwendet.
Der Standardsatz von Single-Qubit Clifford-Toren, standardmäßig enthalten in Q#, enthalten
$$H=\frac{{2}}\begin{bmatrix}{1}{\sqrt{ 1 & 1 1 \\ &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 0 \\ & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 1 \\& 0 \end{bmatrix}= HT^4H,$$
$$Y =0 amp; -i i &\\ amp; 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1&&\begin{bmatrix} 0 0\\& amp;-1 \end{bmatrix}=T^4. $$
Zusammen mit dem Nicht-Clifford-Tor (dem T-Tor) können diese Vorgänge zusammengesetzt werden, um jede einheitliche Transformation auf einem einzigen Qubit anzunähern.
T-Fabriken im Azure Quantum Resource Estimator
Die Nicht-Clifford T-Torvorbereitung ist entscheidend, da die anderen Quantentore für die universelle Quantenberechnung nicht ausreichen. Zur Implementierung von Nicht-Clifford-Operationen für Praktisch-Skalenalgorithmen ist eine niedrige Fehlerrate T-Gates (oder T-Zustände) erforderlich. Sie können jedoch schwierig sein, direkt auf logische Qubits zu implementieren, und kann auch für einige physische Qubits schwierig sein.
In einem fehlertoleranten Quantencomputer werden die erforderlichen niedrigen Fehlerraten-T-Zustände mit einer T-Zustandsdestillationsfabrik oder einer T-Fabrik für kurze Zeit produziert. Diese T-Fabriken umfassen in der Regel eine Abfolge von Destillationsrunden, wobei jede Runde viele laute T-Zustände einnimmt, die in einem kleineren Entfernungscode codiert sind, verarbeitet sie mithilfe einer Destillationseinheit und gibt weniger rauschende T-Zustände aus, die in einem größeren Abstandscode codiert sind, wobei die Anzahl der Runden, Destillationseinheiten und Entfernungen alle Parameter unterschiedlich sein kann. Dieses Verfahren wird durchlaufen, wobei die Ausgabe-T-Zustände einer Runde als Eingaben in die nächste Runde eingespeist werden.
Basierend auf der Dauer der T-Factory bestimmt der Azure Quantum Resource Estimator , wie oft eine T-Factory aufgerufen werden kann, bevor sie die Gesamtlaufzeit des Algorithmus überschreitet und so viele T-Zustände während der Algorithmuslaufzeit erzeugt werden können. In der Regel sind mehr T-Zustände erforderlich als die, die innerhalb der Aufrufe einer einzelnen T-Factory während der Algorithmuslaufzeit erzeugt werden können. Um weitere T-Zustände zu erzeugen, verwendet der Ressourcen-Estimator Kopien der T-Fabriken.
Physische T-Werksschätzung
Der Ressourcen-Estimator berechnet die Gesamtanzahl der T-Zustände, die zum Ausführen des Algorithmus erforderlich sind, und die Anzahl der physischen Qubits für eine einzelne T-Factory und deren Laufzeit.
Ziel ist es, alle T-Zustände innerhalb der Algorithmuslaufzeit mit so wenigen T Factory-Kopien wie möglich zu produzieren. Das folgende Diagramm zeigt ein Beispiel für die Laufzeit des Algorithmus und die Laufzeit einer T-Factory. Sie können sehen, dass die Laufzeit der T-Factory kürzer als die Laufzeit des Algorithmus ist. In diesem Beispiel kann eine T-Fabrik einen T-Zustand destillieren. Zwei Fragen stellen sich:
- Wie oft kann die T-Factory vor dem Ende des Algorithmus aufgerufen werden?
- Wie viele Kopien der T Factory-Destillationsrunde sind erforderlich, um die Anzahl der T-Zustände zu erstellen, die während der Laufzeit des Algorithmus erforderlich sind?
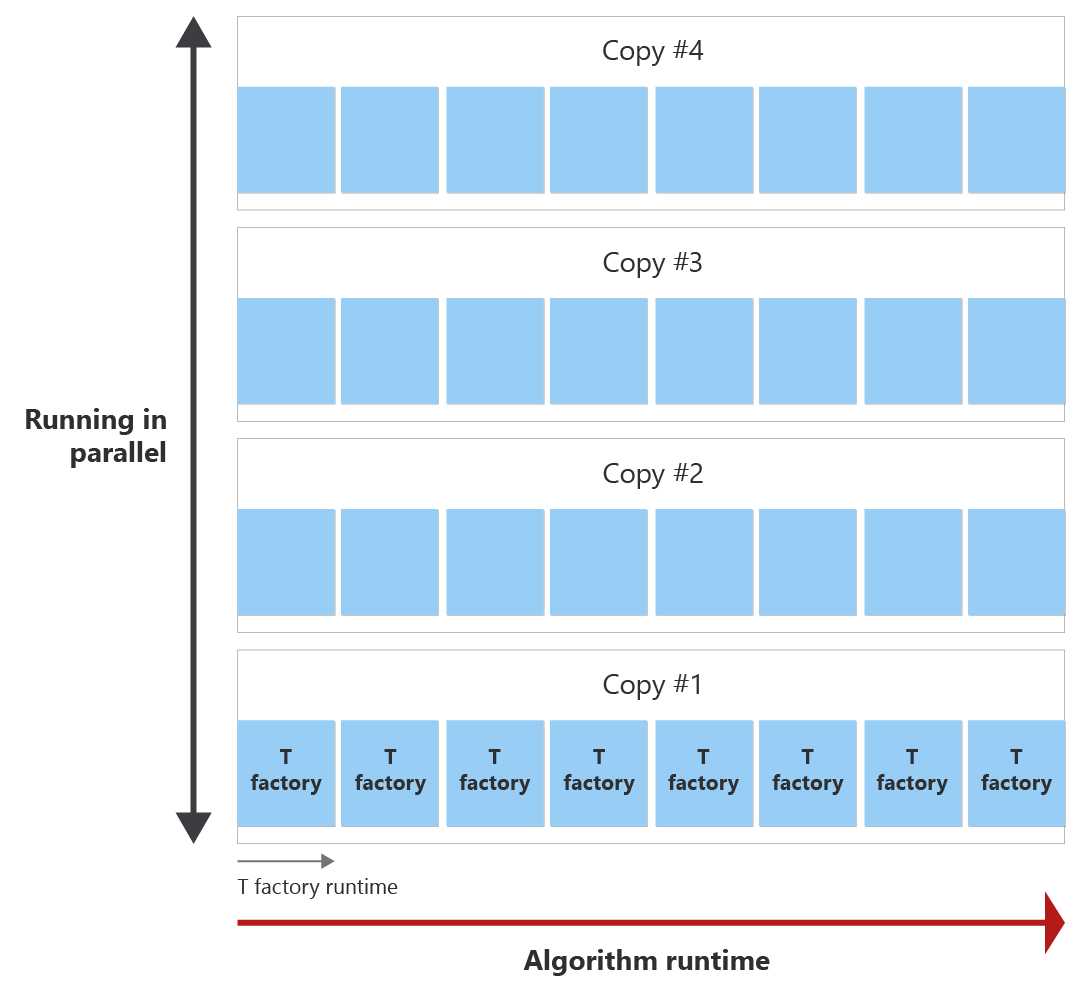
Vor dem Ende des Algorithmus kann die T-Fabrik acht Mal aufgerufen werden, was als Destillationsrunde bezeichnet wird. Wenn Sie z. B. 30 T-Zustände benötigen, wird eine einzelne T-Factory acht Mal während der Laufzeit des Algorithmus aufgerufen und erstellt somit acht T-Zustände. Dann benötigen Sie vier Exemplare der T-Werksdestillation, die parallel zum Destillieren der benötigten 30 T-Zustände ausgeführt wird.
Hinweis
Beachten Sie, dass T-Factorykopien und T-Factoryaufrufe nicht identisch sind.
Die T-Zustandsdestillationsfabriken werden in einer Abfolge von Runden implementiert, wobei jede Runde aus einer Reihe von Kopien von Destillationseinheiten besteht, die parallel ausgeführt werden. Der Ressourcen-Estimator berechnet, wie viele physische Qubits erforderlich sind, um eine T-Factory auszuführen und wie lange die T-Factory ausgeführt wird, unter anderem erforderliche Parameter.
Sie können nur vollständige Aufrufe einer T-Fabrik ausführen. Daher kann es Situationen geben, in denen die akkumulierte Laufzeit aller T-Factoryaufrufe kleiner als die Algorithmuslaufzeit ist. Da Qubits von verschiedenen Runden wiederverwendet werden, ist die Anzahl der physischen Qubits für eine T-Factory die maximale Anzahl physischer Qubits, die für eine Runde verwendet werden. Die Laufzeit der T-Factory ist die Summe der Laufzeit in allen Runden.
Hinweis
Wenn die physische T-Gate-Fehlerrate niedriger als die erforderliche Fehlerrate des logischen T-Zustands ist, kann der Ressourcen-Estimator keine gute Ressourcenschätzung durchführen. Wenn Sie einen Ressourcenschätzungsauftrag übermitteln, tritt möglicherweise auf, dass die T-Factory nicht gefunden werden kann, da die erforderliche Fehlerrate des logischen T-Zustands entweder zu niedrig oder zu hoch ist.
Weitere Informationen finden Sie in Anhang C zur Bewertung der Anforderungen zur Skalierung auf praktischen Quantenvorteil.