Konventionen für Quantenschaltungsdiagramme
Manchmal sind Quantenalgorithmen in einem Schaltkreisdiagramm einfacher zu verstehen als in der entsprechenden schriftlichen Matrixdarstellung. In diesem Artikel wird erläutert, wie Quantenkreisdiagramme und ihre Konventionen gelesen werden.
Weitere Informationen finden Sie unter Visualisieren von Quantenkreisdiagrammen.
Lesen von Quantenkreisdiagrammen
In einer Quantenschaltung fließt die Zeit von links nach rechts. Quantengates sind in chronologischer Reihenfolge angeordnet, wobei das äußerste linke Gate zuerst auf die Qubits angewendet wird.
Nehmen Sie das folgende Quantenschaltungsdiagramm als Beispiel:
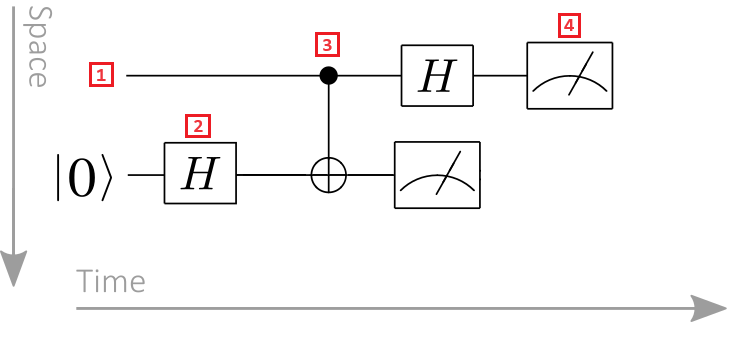
- Qubit-Register: Qubit-Register werden als horizontale Linien angezeigt, wobei jede Zeile ein Qubit darstellt. Die oberste Zeile ist qubit-Register mit der Bezeichnung 0, die zweite Zeile ist qubit register mit der Bezeichnung 1 usw.
- Quantum gate: Quantenoperationen werden durch Quantentore dargestellt. Der Begriff Quantengatter ist eine Analogie zu klassischen Logikgattern. Gates, die auf ein oder mehrere Qubit-Register wirken, werden als Kästchen dargestellt. In diesem Beispiel stellt das Symbol einen Hadamard-Vorgang dar.
- Kontrolliertes Tor: Kontrollierte Tore wirken auf zwei oder mehr Qubits. In diesem Beispiel stellt das Symbol ein CNOT-Gate dar. Der schwarze Kreis stellt das Steuerelement-Qubit dar, und das Kreuz innerhalb eines Kreises stellt den target Qubit dar.
- Messvorgang: Das Metersymbol stellt einen Messvorgang dar. Der Messvorgang nimmt ein Qubit-Register als Eingabe und gibt klassische Informationen aus.
Anwenden von Quantentoren
Da die Zeit von links nach rechts fließt, wird das am weitesten linksste Tor zuerst angewendet. Beispielsweise ist die Aktion des folgenden Quantenkreises die Einheitsmatrix $CBA$.
Hinweis
Für die Matrixmultiplikation gilt die entgegengesetzte Konvention: Die äußerste rechte Matrix wird zuerst angewendet. In Quantenschaltungsdiagrammen wird jedoch zuerst das äußerste linke Gate angewendet. Dieser Unterschied kann manchmal zu Verwirrung führen. Daher ist es wichtig, diesen wesentlichen Unterschied zwischen der linearen algebraischen Notation und Quantenschaltungsdiagrammen zu beachten.
Ein- und Ausgaben von Quantenschaltungen
In einem Quantenschaltungsdiagramm stellen die Kabel, die in ein Quantengate gelangen, die Qubits dar, die in das Quantentor eingegeben werden, und die Kabel, die das Quantentor verlassen, stellen die Qubits dar, die vom Quantentor ausgegeben werden.
Die Anzahl der Eingaben eines Quantumgates entspricht der Anzahl der Ausgaben eines Quantengaters. Dies liegt daran, dass Quantenvorgänge einheitlich und somit umkehrbar sind. Wenn ein Quantentor mehr Ausgaben als Eingaben hatte, wäre es nicht umkehrbar und daher nicht einheitshaft, was ein Widerspruch ist.
Aus diesem Grund gilt für jedes Feld in einem Schaltungsdiagramm, dass die Anzahl der in das Feld hineinführenden Drähte genau mit der Anzahl der aus dem Feld hinausführenden Drähte übereinstimmen muss.
Multi-Qubit-Vorgänge
Für Multi-Qubit-Schaltungsdiagramme gelten die gleichen Konventionen wie für Ein-Qubit-Schaltungsdiagramme. Beispielsweise kann eine zwei-Qubit-Einheitsoperation $B$ (H S\otimes X)$ definiert $werden, sodass die entsprechende Quantenschaltung folgendes ist:
$B$ lässt sich auch als Operation für ein einzelnes Zwei-Qubit-Register statt als Operation für zwei Ein-Qubit-Register auffassen, abhängig von dem Kontext, in dem die Schaltung verwendet wird.
Die vielleicht hilfreichste Eigenschaft dieser abstrakten Schaltungsdiagramme ist, dass sie eine allgemeine Beschreibung komplexer Quantenalgorithmen ermöglichen, ohne elementare Gates darstellen zu müssen. So können Sie eine Vorstellung vom Datenfluss für einen großen Quantenalgorithmus erhalten, ohne alle Details der einzelnen Unterroutinen innerhalb des Algorithmus verstehen zu müssen.
Kontrollierte Gates
Quantengesteuerte Tore sind Zwei-Qubit-Tore, die ein Ein-Qubit-Gate auf ein target Qubit anwenden, wenn sich ein Kontroll-Qubit in einem bestimmten Zustand befindet.
Betrachten Sie z. B. ein quantengesteuertes Tor, das $\Lambda(G)$ bezeichnet wird, wobei der Wert eines einzelnen Qubits die Anwendung des $G-Vorgangs$ steuert. Das kontrollierte Tor $\Lambda(G)$ kann verstanden werden, indem man sich das folgende Beispiel einer Produktzustandseingabe ansieht:
$\Lambda(G) (\alpha\ket{{0} + \beta\ket{1}) \ket{\psi}=\alpha\ket{{0}\ket{\psi} + \beta\ket{{1} G\ket{\psi}$
Das bedeutet, dass das kontrollierte Gatter $G$ auf das Register anwendet, das $\psi$ enthält, wenn und nur wenn das steuernde Qubit den Wert $1$ hat. Im Allgemeinen werden solche kontrollierten Vorgänge in Schaltkreisdiagrammen durch das folgende Symbol beschrieben:
Hier gibt der schwarze Kreis das Quantenbit an, durch das das Gate kontrolliert wird, und ein vertikaler Draht gibt die unitäre Operation an, die angewendet wird, wenn das Kontroll-Qubit den Wert $1$ annimmt.
Für die besonderen Fälle, in denen $G=X$ und $G=Z$, die folgende Notation verwendet wird, um die kontrollierte Version der Tore zu beschreiben (beachten Sie, dass das kontrollierte X-Tor das CNOT-Tor ist):
Q# stellt Methoden zum automatischen Generieren der kontrollierten Version einer Operation bereit, sodass der Programmierer diese Operationen nicht selbst codieren muss. Ein Beispiel hierfür wird unten gezeigt:
operation PrepareSuperposition(qubit : Qubit) : Unit
is Ctl { // Auto-generate the controlled specialization of the operation
H(qubit);
}
Klassisch kontrollierte Tore
Quantentore können auch nach einer Messung angewendet werden, wo das Ergebnis der Messung als klassisches Kontrollbit fungiert.
Das folgende Symbol stellt ein klassisch kontrolliertes Tor dar, bei dem $G$ auf das klassische Kontrollbit angewendet wird, das wert $1$ ist:
Messungsoperator
Messvorgänge nehmen ein Qubit-Register, misst es und gibt das Ergebnis als klassische Informationen aus.
Eine Messungsoperation wird durch ein Messgerätsymbol dargestellt. Sie akzeptiert als Eingabe immer ein Qubit-Register (durch eine durchgezogene Linie dargestellt) und gibt klassische Informationen aus (durch eine doppelte Linie dargestellt). Insbesondere sieht das Symbol des Messvorgangs wie folgt aus:
In Q#, der Measure Operator implementiert den Messvorgang.
Beispiel: Unitäre Transformation
Ziehen Sie die unitäre Transformation $\text{ CNOT}_{01}(H\otimes 1)$ in Betracht. Diese Gatesequenz ist für Quantencomputing von grundlegender Bedeutung, da sie einen maximal verschränkten Zwei-Qubit-Zustand erzeugt:
$\mathrm{CNOT}_{01}(H\otimes 1)\ket{00}=\frac{1}{\sqrt{2}}\left(\ket{{00} + \ket{11}\right),$
Operationen mit dieser oder höherer Komplexität sind in Quantenalgorithmen und der Quantenfehlerkorrektur weit verbreitet.
Das Schaltungsdiagramm zum Erzeugen dieses maximal verschränkten Quantenzustands sieht folgendermaßen aus:
Das Symbol hinter dem Hadamard-Tor stellt ein CNOT-Tor dar, bei dem der schwarze Kreis das Steuerqubit angibt und das Kreuz innerhalb eines Kreises den target Qubit angibt. Diese Quantenschaltung wird als auf zwei Qubits (oder entsprechend zwei Register, die aus jeweils einem Qubit bestehen) wirkende Schaltung dargestellt.
Beispiel: Teleportation-Schaltkreisdiagramm
Die Quantenteleportation ist einer der besten Quantenalgorithmus zur Veranschaulichung von Schaltkreiskomponenten.
Die Quantenteleportation ist ein Protokoll, das es ermöglicht, einen Quantenzustand von einem Qubit in einen anderen zu übertragen, mit Hilfe eines geteilten verangten Zustands zwischen dem Absender und Empfänger und der klassischen Kommunikation zwischen ihnen.
Zu Lernzwecken heißt der Absender Alice, der Empfänger heißt Bob, und der qubit, der teleportiert werden soll, wird als Nachrichten-Qubit bezeichnet. Alice und Bob halten jeweils einen Qubit, und Alice hat ein zusätzliches Qubit, das ist der Nachrichten-Qubit.
Das folgende Schaltkreisdiagramm veranschaulicht das Teleportation-Protokoll:
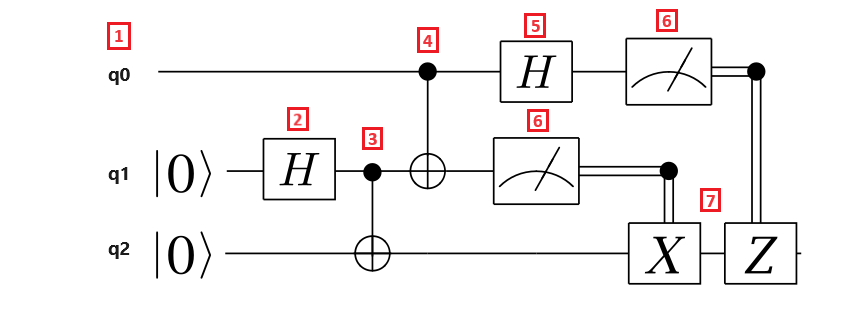
Lassen Sie uns die Schritte des Teleportationsprotokolls aufschlüsseln:
- Qubit register q0 is the message qubit, qubit register q1 is Alice's qubit, and qubit register q2 is Bob es qubit. Der Nachrichten-Qubit befindet sich in einem unbekannten Zustand, und Alice und Bobs Qubits befinden sich im $\ket{0}$ Zustand.
- Ein Hadamard-Tor wird auf Alices Qubit angewendet. Da sich das Qubit im $\ket{0}$ Zustand befindet, ist{2}}$\frac{1}{\sqrt{ der resultierende Zustand ( + \ket{1}\ket{{0} )$.
- Ein CNOT-Gate wird auf Alice und Bobs Qubits angewendet. Alices Qubit ist der Steuer-Qubit, und Bobs Qubit ist der target Qubit. Der resultierende Zustand ist $\frac{{1}{\sqrt{2}}(\ket{00} + \ket{{11})$. Alice und Bob teilen nun einen verangten Zustand.
- Ein CNOT-Gate wird auf den Nachrichten qubit und Alices Qubit angewendet. Da Alices Qubit auch mit Bobs Qubit verangt ist, ist der resultierende Zustand ein drei-qubit-verangter Zustand.
- Ein Hadamard-Gate wird auf das Nachrichten-Qubit angewendet.
- Alice misst ihre beiden Qubits und teilt den Messergebnissen Bob mit, was nicht in der Schaltung widerspiegelt wird. Die Messergebnisse sind zwei klassische Bits, die die Werte 00, 01, 10 oder 11 annehmen können.
- Zwei klassisch kontrollierte Pauli-Tore X und Z werden abhängig vom Ergebnisbitwert $1$ auf Bobs Qubit angewendet. Der resultierende Zustand ist der ursprüngliche Nachrichten qubit-Zustand.