Theorie des Grover-Suchalgorithmus
Dieser Artikel bietet eine ausführliche theoretische Erläuterung der mathematischen Prinzipien, die dem Grover-Algorithmus zugrunde liegen.
Eine praktische Implementierung des Grover-Algorithmus zur Lösung mathematischer Probleme finden Sie im Suchalgorithmus von Implement Grover.
Problembeschreibung
Der Algorithmus von Grover beschleunigt die Lösung für unstrukturierte Datensuchen (oder Suchprobleme), die Suche in weniger Schritten als jeder klassische Algorithmus ausführen könnte. Jede Suchaufgabe kann mit einer abstrakten Funktion $f(x)$ formuliert werden, die Suchelemente $x$ akzeptiert. Wenn das Element $x$ eine Lösung für die Suchaufgabe ist, dann ist $f(x)=1$. Wenn das Element $x$ keine Lösung ist, dann ist $f(x)=0$. Das Suchproblem besteht darin, nach jedem Element $x_0$ zu suchen, für das $f(x_0)=1$ ist.
In der Tat, jedes Problem, mit dem Sie überprüfen können, ob ein bestimmter Wert $x$ eine gültige Lösung ist (ein &Quot; Ja oder kein Problem") kann in Bezug auf das Suchproblem formuliert werden. Hier einige Beispiele:
- Boolesche Sättigungsproblem: Ist der Satz boolescher Werte $x$ eine Interpretation (eine Zuordnung von Werten zu Variablen), die die angegebene boolesche Formel erfüllt?
- Problem mit Dem Verkäufer: Beschreibt $x$ die kürzeste mögliche Schleife, die alle Städte verbindet?
- Datenbanksuchproblem: Enthält die Datenbanktabelle einen Datensatz $x$?
- Ganzzahlige Faktorisierungsproblem: Ist die feste Zahl $N$ divisierbar durch die Zahl $x$?
Das durch den Grover-Algorithmus zu lösenden Problem kann wie folgt ausgedrückt werden: Suche für eine klassische Funktion $f(x):\{0,1\}^n \rightarrow\{0,1\}$, in der $n$ die Bit-Größe des Suchraums ist, eine Eingabe $x_0$, für die $f(x_0)=1$ ist. Die Komplexität des Algorithmus wird anhand der Häufigkeit der Verwendungen der Funktion $f(x)$ gemessen. Herkömmlicherweise muss $f(x)$ im schlechtesten Fall insgesamt $N-1$ Male ausgewertet werden, wobei $N=2^n$ gilt und alle Möglichkeiten ausprobiert werden. Nach $N-1$ Elementen steht fest, dass es sich um das letzte Element handeln muss. Mit dem Grover-Quantenalgorithmus kann dieses Problem viel schneller gelöst werden, da er eine quadratische Beschleunigung ermöglicht. Quadratisch bedeutet hier, dass nur ungefähr $\sqrt{N}$ Auswertungen statt $N$ Auswertungen erforderlich sind.
Übersicht über den Algorithmus
Angenommen, es sind $N=2^n$ geeignete Elemente für die Suchaufgabe vorhanden, und sie werden indiziert, indem jedem Element eine ganze Zahl zwischen $0$ und $N-1$ zugewiesen wird. Nehmen wir außerdem an, dass es $M$ unterschiedliche gültige Eingaben gibt, sodass $M$ Eingaben vorhanden sind, für die $f(x)=1$ gilt. Die Schritte des Algorithmus lauten dann wie folgt:
- Er beginnt mit einem Register von $n$ Qubits, die mit dem Zustand $\ket{0}$ initiiert werden.
- Bereiten Sie das Register in einer einheitlichen Superposition vor, indem Sie $H$ auf jedes Qubit im Register anwenden: $$|\text{register}\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x\rangle$$
- Wenden Sie die folgenden Vorgänge auf das Register $N_{\text{Optimalzeiten}}$ an:
- Das Phasenorakel $O_f$, das die bedingte Phasenverschiebung $–1$ für die Lösungselemente anwendet.
- Wenden Sie $H$ auf jedes Qubit im Register an.
- Die bedingte Phasenverschiebung $–1$ auf jeden Berechnungsbasiszustand mit Ausnahme von $\ket{0}$. Dies kann durch die unitäre Operation $-O_0$ dargestellt werden, da $O_0$ nur die bedingte Phasenverschiebung auf $\ket{0}$ darstellt.
- Wenden Sie $H$ auf jedes Qubit im Register an.
- Messen Sie das Register, um den Index eines Elements zu erhalten, das eine Lösung mit sehr hoher Wahrscheinlichkeit ist.
- Überprüfen Sie, ob es sich um eine gültige Lösung handelt. Falls nicht, starten Sie erneut.
$N_\text{optimal}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{{2}\right\rfloor$ ist die optimale Anzahl von Iterationen, die die Wahrscheinlichkeit erhöht, durch Messen des Registers das richtige Element zu erhalten.
Hinweis
Die gemeinsame Anwendung der Schritte 3.b, 3.c und 3.d ist in der Literatur üblicherweise als Grover-Diffusionsoperator bekannt.
Die gesamte unitäre Operation, die auf das Register angewendet wird, lautet:
$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$
Schrittweises Verfolgen des Zustands des Registers
Zur Veranschaulichung des Prozesses verfolgen wir die mathematischen Transformationen des Zustands des Registers in einem einfachen Fall, in dem nur zwei Qubits vorhanden sind und das gültige Element $\ket{01} lautet.$
Das Register hat am Anfang den folgenden Zustand: $$|\text{register}\rangle=|00\rangle$$
Nach dem Anwenden von $H$ auf jedes Qubit lautet der Zustand des Registers: $$|\text{register}\rangle=\frac{{1}{\sqrt{{4}}\sum_{i \in \{0,1\}^2}|i\rangle=\frac12(\ket{00}+\ket{01}+\ket{10}+\ket{11})$$
Anschließend wird das Phasenorakel angewendet, um Folgendes abzurufen: $$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}+\ket{{11})$$
$H$ wirkt dann erneut auf jedes Qubit, mit dem Ergebnis: $$|\text{register}\rangle=\frac12(\ket{{00}+\ket{{01}-\ket{{10}+\ket{{11})$$
Jetzt wird die bedingte Phasenverschiebung auf jeden Zustand angewendet, mit Ausnahme von $\ket{00}$$$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}-\ket{{11})$$
Die erste Grover-Iteration wird dann beendet, indem erneut $H$ angewendet wird, um Folgendes zu erhalten: $$|\text{register}\rangle=\ket{{01}$$
Bei Ausführung der obigen Schritte wird das gültige Element mit nur einer Iteration gefunden. Wie Sie später sehen werden, liegt dies daran, dass für N=4 und ein einzelnes gültiges Element $N_\text{optimal}=1$.
Geometrische Erklärung
Um den Grover-Algorithmus zu begreifen, untersuchen wir ihn aus geometrischer Sicht. $\ket{\text{}}$ sei die Superposition aller Zustände, die keine Lösung für das Suchproblem darstellen. Angenommen, es gibt $M$ gültige Lösungen:
$$\ket{\text{bad}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$
Der Zustand $\ket{\text{good}}$ wird als Superposition aller Zustände definiert, die eine Lösung für das Suchproblem darstellen:
$$\ket{\text{good}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$
Da good und bad sich gegenseitig ausschließen, weil ein Element nicht gleichzeitig gültig und ungültig sein kann, sind die Zustände $\ket{\text{good}}$ und $\ket{\text{bad}}$ orthogonal. Beide Zustände bilden die orthogonale Basis einer Ebene im Vektorraum. Diese Ebene kann zum Visualisieren des Algorithmus verwendet werden.
Angenommen, $\ket{\psi}$ ist ein beliebiger Zustand in der Ebene, die von $\ket{\text{good}}$ und $\ket{\text{bad}}$ gebildet wird. Jeder Zustand in dieser Ebene kann wie folgt ausgedrückt werden:
$$\ket{\psi}=\alpha\ket{\text{good}} + \beta\ket{\text{bad}}$$
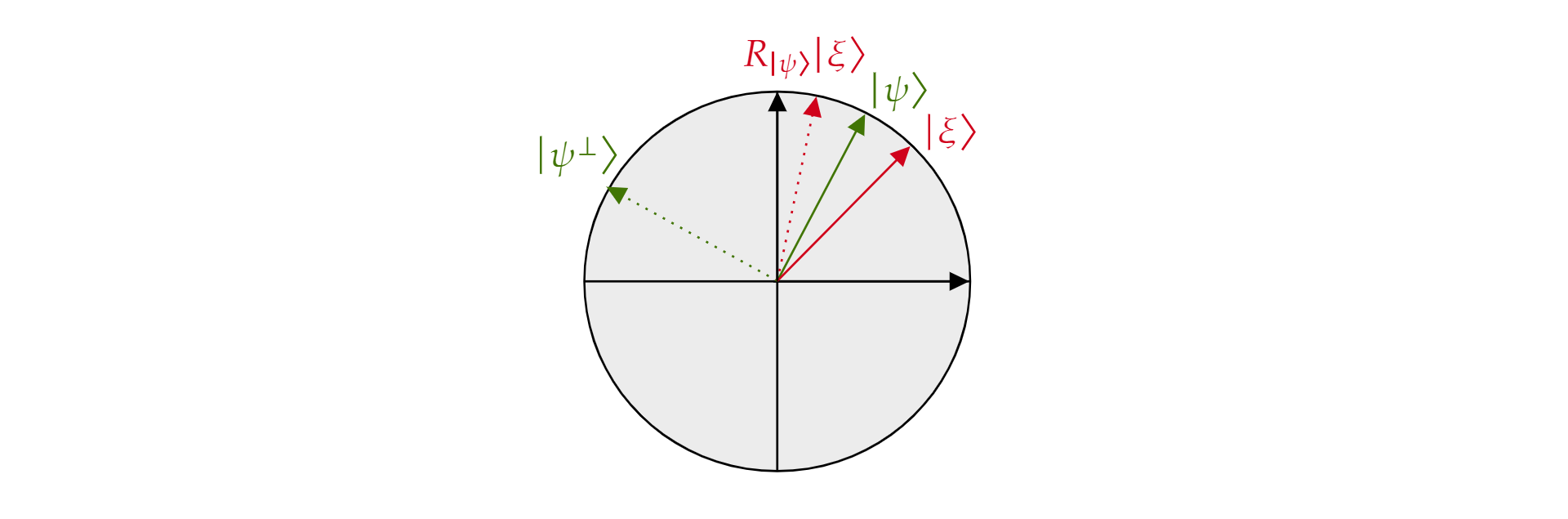
wobei $\alpha$ und $\beta$ reelle Zahlen sind. Jetzt führen wir den Reflexionsoperator $R_{\ket{\psi}}$ ein, wobei $\ket{\psi}$ ein beliebiger Qubitzustand in der Ebene ist. Der Operator ist wie folgt definiert:
$$R_{\ket{\psi}}=2\ket{\psi}\bra{\psi}-\mathcal{I}$$
Er wird als Reflexionsoperator für $\ket{\psi}$ bezeichnet, da er geometrisch als Reflexion um die Richtung $\ket{\psi}$ interpretiert werden kann. Um ihn zu ermitteln, verwenden Sie die orthogonale Basis der von $\ket{\psi}$ gebildeten Ebene und die orthogonale Ergänzung $\ket{\psi^{\perp}}$. Jeder Zustand $\ket{\xi}$ der Ebene lässt sich in eine solche Basis zerlegen:
$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$
Bei Anwendung des Operators $R_{\ket{\psi}}$ auf $\ket{\xi}$:
$$R_{\ket{\psi}}\ket{\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$
Der Operator $R_\ket{\psi}$ bewirkt eine Umkehrung der orthogonalen Ergänzung in $\ket{\psi}$, lässt jedoch die Komponente $\ket{\psi}$ unverändert. Somit ist $R_\ket{\psi}$ eine Reflexion um $\ket{\psi}$.
Der Grover-Algorithmus beginnt nach der ersten Anwendung von $H$ auf jedes Qubit mit einer einheitlichen Superposition aller Zustände. Dies kann wie folgt ausgedrückt werden:
$$\ket{\text{all}}=\sqrt{\frac{M}{N}}\ket{\text{good}} + \sqrt{\frac{N-M}{N}}\ket{\text{bad}}$$
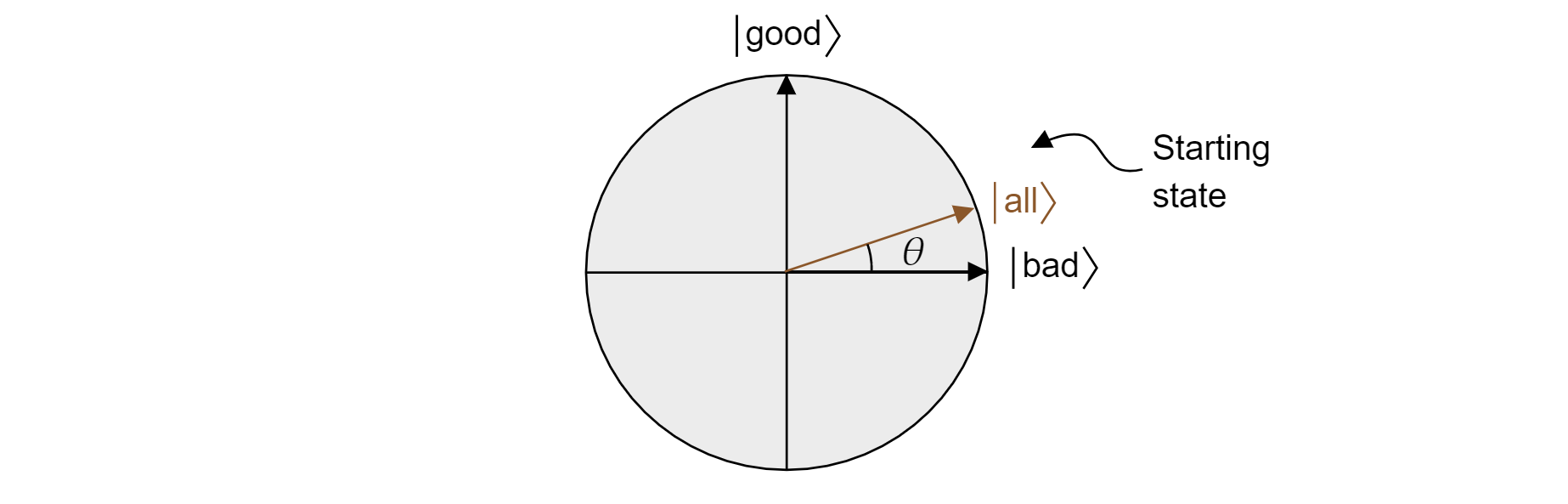
Und somit ist der Zustand in der Ebene vorhanden. Beachten Sie, dass die Wahrscheinlichkeit, ein richtiges Ergebnis zu erhalten, beim Messen der gleichen Superposition nur $|\braket{\text{gut}|{\text{alle}}}|^2=M/N$ ist, was Sie von einer zufälligen Vermutung erwarten würden.
Mit dem Orakel $O_f$ wird jeder Lösung des Suchproblems eine negative Phase hinzugefügt. Es lässt sich somit als Reflexion um die Achse $\ket{\text{bad}}$ ausdrücken:
$$O_f = R_{\ket{\text{bad}}}= 2\ket{\text{bad}}\bra{\text{bad}} - \mathcal{I}$$
Analog dazu ist die bedingte Phasenverschiebung $O_0$ eine umgekehrte Reflexion um den Zustand $\ket{0}$:
$$O_0 = R_{\ket{0}}= -2\ket{{0}\bra{0} + \mathcal{I}$$
Davon ausgehend lässt sich einfach nachweisen, dass die Grover-Diffusionsoperation $-H^{\otimes n} O_0 H^{\otimes n}$ eine Reflexion um den Zustand $\ket{all}$ ist. Die entsprechende Formel lautet:
$$-H^{\otimes n} O_0 H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{{0}H^{\otimes n} -H^{\otimes n}\mathcal{I}H^{\otimes n}= 2\ket{\text{all}}\bra{\text{all}} - \mathcal{I}= R_{\ket{\text{all}}}$$
Es wurde gezeigt, dass jede Iteration des Grover-Algorithmus aus den beiden Reflexionen $R_\ket{\text{bad}}$ und $R_\ket{\text{all}}$ besteht.
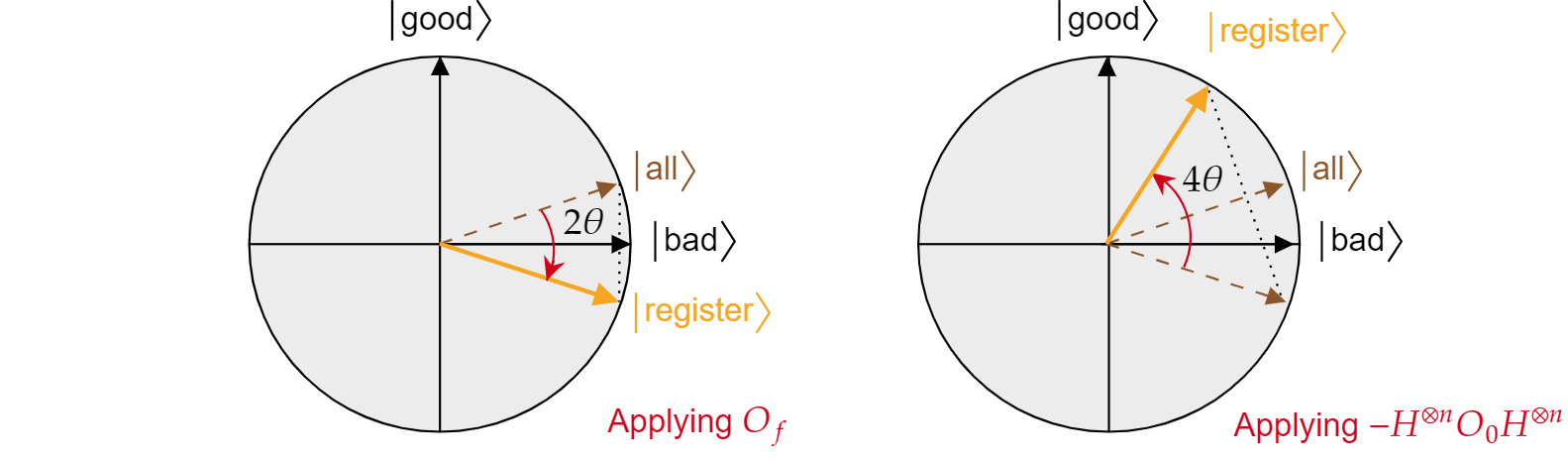
Die kombinierte Auswirkung jeder Grover-Iteration ist eine Drehung um den Winkel $2\theta$ gegen den Uhrzeigersinn. Glücklicherweise lässt sich der Winkel $ \theta$ einfach ermitteln. Da $\theta$ nur der Winkel zwischen $\ket{\text{all}}$ und $\ket{\text{bad}}$ ist, kann der Winkel über das Skalarprodukt ermittelt werden. Da bekannt ist, dass $\cos{\theta}=\braket{\text{all}|\text{bad}}$ gilt, muss $\braket{\text{all}|\text{bad}}$ berechnet werden. Aus der Aufteilung von $\ket{\text{all}}$ in $\ket{\text{bad}}$ und $\ket{\text{good}}$ folgt:
$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$
Der Winkel zwischen dem Zustand des Registers und dem $\ket{\text{guten}}$ Zustand nimmt bei jeder Iteration ab, was zu einer höheren Wahrscheinlichkeit zur Messung eines gültigen Ergebnisses führt. Um diese Wahrscheinlichkeit zu berechnen, müssen Sie lediglich ein gutes}|\text{Register}}|^2$ berechnen$|\braket{\text{. Der Winkel zwischen $\ket{\text{good}}$ und $\ket{\text{register}}$$\gamma (k)$ wird angegeben, wobei $k$ für die Iterationsanzahl steht:
$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$
Daher lautet die Erfolgswahrscheinlichkeit:
$$P(\text{success}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$
Optimale Anzahl von Iterationen
Da die Erfolgswahrscheinlichkeit als Funktion der Anzahl von Iterationen ausgedrückt werden kann, lässt sich die optimale Anzahl $N_{\text{optimal}}$ von Iterationen ermitteln, indem die kleinste positive ganze Zahl berechnet wird, die für die Funktion für die Erfolgswahrscheinlichkeit zu einer Maximierung führt (näherungsweise).
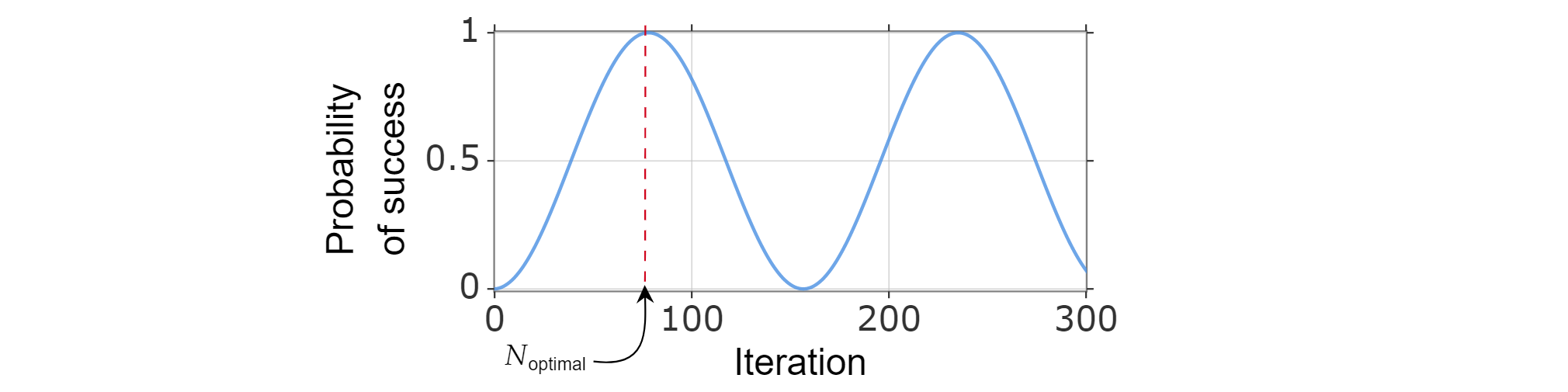
Da bekannt ist, dass $\sin^2{x}$ das erste Maximum für $x=\frac{\pi erreicht}{2}$, gilt Folgendes:
$$\frac{\pi}{{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$
Dies ergibt:
$$k_{\text{optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 =\frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N}\right)$$
Für den letzten Schritt gilt $\arccos \sqrt{1-x}=\sqrt{x} + O(x^{3/2})$.
Daher können Sie N_Optimal auswählen, um N_\text{optimal\left}=\lfloor \frac{\pi{4}\sqrt{\frac{}{N}{M}}-{1}{2}\frac{\right\rfloor$ zu sein.$$}$\text{
Komplexitätsanalyse
Basierend auf der vorherigen Analyse sind $O\left(\sqrt{\frac{N}{M}}\right)$ Abfragen des Orakels $O_f$ erforderlich, um ein gültiges Element zu finden. Kann der Algorithmus jedoch hinsichtlich der Zeitkomplexität effizient implementiert werden? $O_0$ basiert auf der Berechnung boolescher Operationen für $n$ Bits und kann mithilfe von $O(n)$ Gates implementiert werden. Es sind auch zwei Ebenen mit $n$ Hadamard-Gates vorhanden. Beide Komponenten erfordern daher nur $O(n)$ Gates pro Iteration. Aus $N=2^n$ folgt $O(n)=O(log(N))$. Wenn $O\left(\sqrt{\frac{N}{M}}\right)$ Iterationen und $O(log(N))$ Gates pro Iteration erforderlich sind, beträgt somit die Gesamtzeitkomplexität (ohne Berücksichtigung der Orakelimplementierung) $O\left(\sqrt{\frac{N}{M}}log(N)\right)$.
Die Gesamtkomplexität des Algorithmus hängt letztendlich von der Komplexität der Implementierung des Oracle $O_f$ ab. Wenn eine Funktionsauswertung auf einem Quantencomputer viel komplizierter ist als auf einem klassischen Computer, wird die Gesamtalgorithmuslaufzeit im Quantenfall länger sein, obwohl technisch weniger Abfragen verwendet werden.
References
Weitere Informationen über den Grover-Algorithmus finden Sie in den folgenden Quellen:
- Ursprünglicher Aufsatz von Lov K. Grover
- Abschnitt "Quantensuchalgorithmen" von Nielsen, M. A. &Ampere; Chuang, I. L. (2010). Quantum Computation and Quantum Information
- Grover-Algorithmus auf Arxiv.org