พัฒนา ประเมิน และให้คะแนนแบบจําลองการคาดการณ์สําหรับยอดขายในซูเปอร์สโตร์
บทช่วยสอนนี้แสดงตัวอย่างแบบ end-to-end ของเวิร์กโฟลว์ Synapse Data Science ใน Microsoft Fabric สถานการณ์สมมติจะสร้างแบบจําลองการคาดการณ์ที่ใช้ข้อมูลยอดขายในอดีตเพื่อคาดการณ์ยอดขายตามหมวดหมู่ผลิตภัณฑ์ในร้านชั้นบนสุด
การคาดการณ์เป็นสินทรัพย์สําคัญในการขาย ซึ่งจะรวมข้อมูลในอดีตและวิธีการทํานายเพื่อให้ข้อมูลเชิงลึกในแนวโน้มในอนาคต การคาดการณ์สามารถวิเคราะห์ยอดขายในอดีตเพื่อระบุรูปแบบ และเรียนรู้จากพฤติกรรมของผู้บริโภคเพื่อปรับกลยุทธ์สินค้าคงคลัง การผลิต และการตลาดให้เหมาะสม วิธีการเชิงรุกนี้ช่วยเพิ่มความสามารถในการปรับตัว การตอบสนอง และประสิทธิภาพโดยรวมของธุรกิจในตลาดแบบไดนามิก
บทช่วยสอนนี้ครอบคลุมขั้นตอนเหล่านี้:
- โหลดข้อมูล
- ใช้การวิเคราะห์ข้อมูลการสํารวจเพื่อทําความเข้าใจและประมวลผลข้อมูล
- ฝึกแบบจําลองการเรียนรู้ของเครื่องด้วยแพคเกจซอฟต์แวร์โอเพนซอร์สและติดตามการทดลองด้วย MLflow และคุณลักษณะการล็อกอัตโนมัติ Fabric
- บันทึกแบบจําลองการเรียนรู้ของเครื่องขั้นสุดท้ายและคาดการณ์
- แสดงประสิทธิภาพของแบบจําลองด้วยการแสดงภาพ Power BI
ข้อกําหนดเบื้องต้น
รับ การสมัครใช้งาน Microsoft Fabric หรือลงทะเบียนสําหรับ Microsoft Fabric รุ่นทดลองใช้ฟรี
ลงชื่อเข้าใช้ Microsoft Fabric
ใช้ตัวสลับประสบการณ์การใช้งานที่ด้านล่างซ้ายของหน้าหลักของคุณเพื่อเปลี่ยนเป็น Fabric

- หากจําเป็น ให้สร้าง Microsoft Fabric lakehouse ตามที่อธิบายไว้ใน สร้างเลคเฮ้าส์ใน Microsoft Fabric
ติดตามในสมุดบันทึก
คุณสามารถเลือกหนึ่งในตัวเลือกเหล่านี้เพื่อติดตามในสมุดบันทึกได้:
- เปิดและเรียกใช้สมุดบันทึกที่มีอยู่ภายในในประสบการณ์วิทยาศาสตร์ข้อมูล Synapse
- อัปโหลดสมุดบันทึกของคุณจาก GitHub ไปยังประสบการณ์วิทยาศาสตร์ข้อมูล Synapse
เปิดสมุดบันทึกที่มีอยู่แล้วภายใน
ตัวอย่าง การคาดการณ์ยอดขาย สมุดบันทึกจะมาพร้อมกับบทช่วยสอนนี้
เมื่อต้องการเปิดสมุดบันทึกตัวอย่างสําหรับบทช่วยสอนนี้ ให้ทําตามคําแนะนําใน เตรียมระบบของคุณสําหรับบทช่วยสอนวิทยาศาสตร์ข้อมูล
ตรวจสอบให้แน่ใจว่า แนบ lakehouse เข้ากับ สมุดบันทึกก่อนที่คุณจะเริ่มเรียกใช้โค้ด
นําเข้าสมุดบันทึกจาก GitHub
AIsample - Superstore Forecast.ipynb notebook มาพร้อมกับบทช่วยสอนนี้
เมื่อต้องการเปิดสมุดบันทึกที่มาพร้อมกับบทช่วยสอนนี้ ให้ทําตามคําแนะนําใน เตรียมระบบของคุณสําหรับบทช่วยสอนวิทยาศาสตร์ข้อมูล การนําเข้าสมุดบันทึกไปยังพื้นที่ทํางานของคุณ
ถ้าคุณต้องการคัดลอกและวางโค้ดจากหน้านี้ สร้างสมุดบันทึกใหม่
ตรวจสอบให้แน่ใจว่า แนบ lakehouse เข้ากับ สมุดบันทึกก่อนที่คุณจะเริ่มเรียกใช้โค้ด
ขั้นตอนที่ 1: โหลดข้อมูล
ชุดข้อมูลประกอบด้วย 9,995 อินสแตนซ์ของยอดขายของผลิตภัณฑ์ต่าง ๆ นอกจากนี้ยังมีแอตทริบิวต์ 21 รายการ ตารางนี้มาจากไฟล์ Superstore.xlsx ที่ใช้ในสมุดบันทึกนี้:
| ID แถว | รหัสคําสั่งซื้อ | วันที่สั่งซื้อ | วันที่จัดส่ง | โหมดการจัดส่ง | รหัสลูกค้า | ชื่อลูกค้า | ปล้อง | ประเทศ | เมือง | สภาพ | รหัสไปรษณีย์ | บริเวณ | รหัสผลิตภัณฑ์ | ประเภท | Sub-Category | ชื่อผลิตภัณฑ์ | ขาย | ปริมาณ | ส่วนลด | กําไร |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | US-2015-108966 | 2015-10-11 | 2015-10-18 | คลาสมาตรฐาน | SO-20335 | Sean O'Donnell | ผู้บริโภค | สหรัฐอเมริกา | ฟอร์ตลอเดอร์เดล | ฟลอริดา | 33311 | ใต้ | FUR-TA-10000577 | เครื่องเรือน | ตาราง | Bretford CR4500 Series ตารางสี่เหลี่ยมบาง ๆ | 957.5775 | 5 | 0.45 | -383.0310 |
| 11 | CA-2014-115812 | 2014-06-09 | 2014-06-09 | คลาสมาตรฐาน | คลาสมาตรฐาน | โบรสีนา ฮอฟฟแมน | ผู้บริโภค | สหรัฐอเมริกา | ลอสแอนเจลิส | แคลิฟอร์เนีย | 90032 | ตะวันตก | FUR-TA-10001539 | เครื่องเรือน | ตาราง | ตารางการประชุมสี่เหลี่ยม Chromcraft | 1706.184 | 9 | 0.2 | 85.3092 |
| 31 | US-2015-150630 | 2015-09-17 | 2015-09-21 | คลาสมาตรฐาน | TB-21520 | แทรซี่ บลูมสไตน์ | ผู้บริโภค | สหรัฐอเมริกา | ฟิลาเดลเฟีย | เพนซิลวาเนีย | 19140 | ตะวันออก | OFF-EN-10001509 | อุปกรณ์สํานักงาน | ซอง จดหมาย | ซองจดหมายผูกสตริงโพลี | 3.264 | 2 | 0.2 | 1.1016 |
กําหนดพารามิเตอร์เหล่านี้เพื่อให้คุณสามารถใช้สมุดบันทึกนี้กับชุดข้อมูลที่แตกต่างกันได้:
IS_CUSTOM_DATA = False # If TRUE, the dataset has to be uploaded manually
IS_SAMPLE = False # If TRUE, use only rows of data for training; otherwise, use all data
SAMPLE_ROWS = 5000 # If IS_SAMPLE is True, use only this number of rows for training
DATA_ROOT = "/lakehouse/default"
DATA_FOLDER = "Files/salesforecast" # Folder with data files
DATA_FILE = "Superstore.xlsx" # Data file name
EXPERIMENT_NAME = "aisample-superstore-forecast" # MLflow experiment name
ดาวน์โหลดชุดข้อมูลและอัปโหลดไปยัง lakehouse
รหัสนี้จะดาวน์โหลดเวอร์ชันสาธารณะของชุดข้อมูล และจากนั้นเก็บไว้ใน Fabric lakehouse:
สําคัญ
อย่าลืม เพิ่มเลคเฮาส์ ลงในสมุดบันทึกก่อนที่คุณจะเรียกใช้ มิฉะนั้น คุณจะได้รับข้อผิดพลาด
import os, requests
if not IS_CUSTOM_DATA:
# Download data files into the lakehouse if they're not already there
remote_url = "https://synapseaisolutionsa.blob.core.windows.net/public/Forecast_Superstore_Sales"
file_list = ["Superstore.xlsx"]
download_path = "/lakehouse/default/Files/salesforecast/raw"
if not os.path.exists("/lakehouse/default"):
raise FileNotFoundError(
"Default lakehouse not found, please add a lakehouse and restart the session."
)
os.makedirs(download_path, exist_ok=True)
for fname in file_list:
if not os.path.exists(f"{download_path}/{fname}"):
r = requests.get(f"{remote_url}/{fname}", timeout=30)
with open(f"{download_path}/{fname}", "wb") as f:
f.write(r.content)
print("Downloaded demo data files into lakehouse.")
ตั้งค่าการติดตามการทดลอง MLflow
Microsoft Fabric จะจับค่าของพารามิเตอร์อินพุตและเมตริกเอาต์พุตของแบบจําลองการเรียนรู้ของเครื่องขณะที่คุณฝึกโดยอัตโนมัติ การดําเนินการนี้จะขยายความสามารถในการล็อกอัตโนมัติของ MLflow จากนั้นข้อมูลจะถูกบันทึกไปยังพื้นที่ทํางานซึ่งคุณสามารถเข้าถึงและแสดงภาพด้วย MLflow API หรือการทดลองที่สอดคล้องกันในพื้นที่ทํางาน เมื่อต้องการเรียนรู้เพิ่มเติมเกี่ยวกับ autologging ดู Autologging ใน Microsoft Fabric
เมื่อต้องการปิดการล็อกโดยอัตโนมัติของ Microsoft Fabric ในเซสชันสมุดบันทึก ให้เรียกใช้ mlflow.autolog() และตั้งค่า disable=True:
# Set up MLflow for experiment tracking
import mlflow
mlflow.set_experiment(EXPERIMENT_NAME)
mlflow.autolog(disable=True) # Turn off MLflow autologging
อ่านข้อมูลดิบจากเลคเฮ้าส์
อ่านข้อมูลดิบจากส่วน Files ของเลคเฮ้าส์ เพิ่มคอลัมน์เพิ่มเติมสําหรับส่วนวันที่ที่แตกต่างกัน ข้อมูลเดียวกันถูกใช้เพื่อสร้างตารางส่วนที่แตกต่างที่มีการแบ่งพาร์ติชัน เนื่องจากข้อมูลดิบถูกจัดเก็บเป็นไฟล์ Excel คุณต้องใช้ pandas เพื่ออ่าน:
import pandas as pd
df = pd.read_excel("/lakehouse/default/Files/salesforecast/raw/Superstore.xlsx")
ขั้นตอนที่ 2: ดําเนินการวิเคราะห์ข้อมูลเชิงสํารวจ
นําเข้าไลบรารี
ก่อนการวิเคราะห์ใด ๆ ให้นําเข้าไลบรารีที่จําเป็น:
# Importing required libraries
import warnings
import itertools
import numpy as np
import matplotlib.pyplot as plt
warnings.filterwarnings("ignore")
plt.style.use('fivethirtyeight')
import pandas as pd
import statsmodels.api as sm
import matplotlib
matplotlib.rcParams['axes.labelsize'] = 14
matplotlib.rcParams['xtick.labelsize'] = 12
matplotlib.rcParams['ytick.labelsize'] = 12
matplotlib.rcParams['text.color'] = 'k'
from sklearn.metrics import mean_squared_error,mean_absolute_percentage_error
แสดงข้อมูลดิบ
ตรวจสอบชุดย่อยของข้อมูลด้วยตนเองเพื่อให้เข้าใจชุดข้อมูลได้ดีขึ้นและใช้ฟังก์ชัน display เพื่อพิมพ์ DataFrame นอกจากนี้ มุมมอง Chart ยังสามารถแสดงภาพชุดย่อยของชุดข้อมูลได้อย่างง่ายดาย
display(df)
สมุดบันทึกนี้เน้นไปที่การคาดการณ์ยอดขายประเภท Furniture เป็นหลัก ซึ่งเร่งความเร็วการคํานวณ และช่วยแสดงประสิทธิภาพของแบบจําลอง อย่างไรก็ตาม สมุดบันทึกนี้ใช้เทคนิคที่สามารถปรับเปลี่ยนได้ คุณสามารถขยายเทคนิคเหล่านั้นเพื่อทํานายยอดขายของผลิตภัณฑ์ประเภทอื่น ๆ ได้
# Select "Furniture" as the product category
furniture = df.loc[df['Category'] == 'Furniture']
print(furniture['Order Date'].min(), furniture['Order Date'].max())
ประมวลผลข้อมูลล่วงหน้า
สถานการณ์ทางธุรกิจในโลกแห่งความจริงมักจําเป็นต้องคาดการณ์ยอดขายในสามประเภทที่แตกต่างกัน:
- หมวดหมู่ผลิตภัณฑ์เฉพาะ
- ประเภทลูกค้าเฉพาะ
- ชุดข้อมูลเฉพาะของประเภทผลิตภัณฑ์และประเภทลูกค้า
ก่อนอื่น ให้ปล่อยคอลัมน์ที่ไม่จําเป็นเพื่อทําการประมวลผลข้อมูลล่วงหน้า บางคอลัมน์ (Row ID, Order ID,Customer ID, และ Customer Name) ไม่จําเป็นเนื่องจากไม่มีผลกระทบ เราต้องการคาดการณ์ยอดขายโดยรวมทั่วทั้งรัฐและภูมิภาคสําหรับหมวดหมู่ผลิตภัณฑ์เฉพาะ (Furniture) ดังนั้นเราสามารถวางคอลัมน์ State, Region, Country, Cityและ Postal Code เมื่อต้องการคาดการณ์ยอดขายสําหรับตําแหน่งที่ตั้งหรือหมวดหมู่เฉพาะ คุณอาจจําเป็นต้องปรับปรุงขั้นตอนการประมวลผลล่วงหน้าตามนั้น
# Data preprocessing
cols = ['Row ID', 'Order ID', 'Ship Date', 'Ship Mode', 'Customer ID', 'Customer Name',
'Segment', 'Country', 'City', 'State', 'Postal Code', 'Region', 'Product ID', 'Category',
'Sub-Category', 'Product Name', 'Quantity', 'Discount', 'Profit']
# Drop unnecessary columns
furniture.drop(cols, axis=1, inplace=True)
furniture = furniture.sort_values('Order Date')
furniture.isnull().sum()
ชุดข้อมูลมีโครงสร้างเป็นรายวัน เราต้องสุ่มตัวอย่างบนคอลัมน์ Order Dateเนื่องจากเราต้องการพัฒนาแบบจําลองเพื่อคาดการณ์ยอดขายเป็นรายเดือน
ก่อนอื่น จัดกลุ่มประเภท Furniture ตาม Order Date จากนั้นคํานวณผลรวมของคอลัมน์ Sales สําหรับแต่ละกลุ่มเพื่อกําหนดยอดขายทั้งหมดสําหรับแต่ละค่า Order Date ที่ไม่ซ้ํากัน สุ่มตัวอย่างคอลัมน์ Sales ที่มีความถี่ในการ MS เพื่อรวบรวมข้อมูลตามเดือน สุดท้าย ให้คํานวณค่ายอดขายเฉลี่ยสําหรับแต่ละเดือน
# Data preparation
furniture = furniture.groupby('Order Date')['Sales'].sum().reset_index()
furniture = furniture.set_index('Order Date')
furniture.index
y = furniture['Sales'].resample('MS').mean()
y = y.reset_index()
y['Order Date'] = pd.to_datetime(y['Order Date'])
y['Order Date'] = [i+pd.DateOffset(months=67) for i in y['Order Date']]
y = y.set_index(['Order Date'])
maximim_date = y.reset_index()['Order Date'].max()
แสดงให้เห็นถึงผลกระทบของ Order Date ต่อ Sales สําหรับหมวดหมู่ Furniture:
# Impact of order date on the sales
y.plot(figsize=(12, 3))
plt.show()
ก่อนการวิเคราะห์ทางสถิติใด ๆ คุณต้องนําเข้าโมดูล statsmodels Python ซึ่งมีคลาสและฟังก์ชันสําหรับการประมาณค่าของแบบจําลองทางสถิติจํานวนมาก นอกจากนี้ยังมีชั้นเรียนและฟังก์ชันในการดําเนินการทดสอบทางสถิติและการสํารวจข้อมูลทางสถิติ
import statsmodels.api as sm
ดําเนินการวิเคราะห์ทางสถิติ
ชุดข้อมูลเวลาจะติดตามองค์ประกอบข้อมูลเหล่านี้ในช่วงเวลาที่กําหนด เพื่อกําหนดการเปลี่ยนแปลงขององค์ประกอบเหล่านั้นในรูปแบบชุดข้อมูลเวลา:
ระดับ: คอมโพเนนต์พื้นฐานที่แสดงค่าเฉลี่ยสําหรับช่วงเวลาเฉพาะ
แนวโน้ม: อธิบายว่าชุดข้อมูลเวลาลดลง คงค่าคงที่ หรือเพิ่มขึ้นเมื่อเวลาผ่านไป
Seasonality: อธิบายสัญญาณเป็นครั้งคราวในชุดข้อมูลเวลา และค้นหาการเกิดขึ้นแบบวงจรที่ส่งผลกระทบต่อรูปแบบชุดข้อมูลเวลาที่เพิ่มขึ้นหรือลดลง
เสียง/ที่เหลือ : หมายถึงความผันผวนแบบสุ่มและความผันผวนในข้อมูลอนุกรมเวลาที่แบบจําลองไม่สามารถอธิบายได้
ในโค้ดนี้ คุณสังเกตองค์ประกอบเหล่านั้นสําหรับชุดข้อมูลของคุณหลังจากการประมวลผลล่วงหน้า:
# Decompose the time series into its components by using statsmodels
result = sm.tsa.seasonal_decompose(y, model='additive')
# Labels and corresponding data for plotting
components = [('Seasonality', result.seasonal),
('Trend', result.trend),
('Residual', result.resid),
('Observed Data', y)]
# Create subplots in a grid
fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(12, 7))
plt.subplots_adjust(hspace=0.8) # Adjust vertical space
axes = axes.ravel()
# Plot the components
for ax, (label, data) in zip(axes, components):
ax.plot(data, label=label, color='blue' if label != 'Observed Data' else 'purple')
ax.set_xlabel('Time')
ax.set_ylabel(label)
ax.set_xlabel('Time', fontsize=10)
ax.set_ylabel(label, fontsize=10)
ax.legend(fontsize=10)
plt.show()
พล็อตจะอธิบายกาล แนวโน้ม และเสียงรบกวนในข้อมูลการคาดการณ์ คุณสามารถจับรูปแบบพื้นฐานและพัฒนาแบบจําลองที่ทําให้การทํานายที่ถูกต้องยืดหยุ่นต่อความผันผวนแบบสุ่มได้
ขั้นตอนที่ 3: ฝึกและติดตามแบบจําลอง
หลังจากที่คุณมีข้อมูลที่พร้อมใช้งานแล้ว ให้กําหนดแบบจําลองการคาดการณ์ ในสมุดบันทึกนี้ ใช้แบบจําลองการคาดการณ์ที่เรียกว่า ค่าเฉลี่ยเคลื่อนที่แบบรวมตามฤดูกาลด้วยปัจจัยที่ไม่ธรรมดา (SARIMAX) SARIMAX ได้รวมส่วนประกอบ autoregressive (AR) และค่าเฉลี่ยเคลื่อนที่ (MA) ความแตกต่างตามฤดูกาล และตัวคาดการณ์ภายนอกเพื่อให้การพยากรณ์ที่ถูกต้องและยืดหยุ่นสําหรับชุดข้อมูลเวลา
คุณยังใช้ MLflow และ Fabric autologging เพื่อติดตามการทดลอง ที่นี่โหลดตารางเดลต้าจากเลคเฮ้าส์ คุณอาจใช้ตารางเดลต้าอื่น ๆ ที่พิจารณาว่าเลคเฮาส์เป็นแหล่งข้อมูล
# Import required libraries for model evaluation
from sklearn.metrics import mean_squared_error, mean_absolute_percentage_error
ปรับแต่ง hyperparameters
SARIMAX คํานึงถึงพารามิเตอร์ที่เกี่ยวข้องกับโหมดค่าเฉลี่ยเคลื่อนที่แบบรวมอัตโนมัติ (ARIMA) (p, d, q) และเพิ่มพารามิเตอร์กาล (P, D, Q, s) อาร์กิวเมนต์แบบจําลอง SARIMAX เหล่านี้เรียกว่า ลําดับ
พารามิเตอร์ลําดับ:
p: ลําดับของคอมโพเนนต์ AR ที่แสดงจํานวนการสังเกตที่ผ่านมาในชุดข้อมูลเวลาที่ใช้ในการคาดการณ์ค่าปัจจุบันโดยทั่วไปพารามิเตอร์นี้ควรเป็นจํานวนเต็มที่ไม่ใช่ค่าลบ ค่าทั่วไปอยู่ในช่วงของ
0ถึง3แม้ว่าจะสามารถมีค่าที่สูงขึ้นได้ แต่จะขึ้นอยู่กับลักษณะของข้อมูลเฉพาะ ค่าpที่สูงกว่าจะระบุหน่วยความจําของค่าในแบบจําลองที่ยาวขึ้นd: ลําดับความแตกต่าง แสดงจํานวนครั้งที่ชุดข้อมูลเวลาจําเป็นต้องมีความแตกต่าง เพื่อให้ได้ความเป็นนิ่งพารามิเตอร์นี้ควรเป็นจํานวนเต็มที่ไม่ใช่ค่าลบ ค่าทั่วไปอยู่ในช่วงของ
0ถึง2ค่าdของ0หมายความว่า ชุดข้อมูลเวลาเป็นแบบนิวๆ อยู่แล้ว ค่าที่สูงขึ้นแสดงถึงจํานวนของการดําเนินงานที่แตกต่างกันที่จําเป็นเพื่อให้นิ่งq: ลําดับของคอมโพเนนต์ MA ที่แสดงจํานวนคําข้อผิดพลาดเสียงรบกวนสีขาวที่ผ่านมาที่ใช้เพื่อคาดการณ์ค่าปัจจุบันพารามิเตอร์นี้ควรเป็นจํานวนเต็มที่ไม่ใช่ค่าลบ ค่าทั่วไปอยู่ในช่วงของ
0ถึง3แต่อาจจําเป็นต้องมีค่าที่สูงกว่าสําหรับชุดข้อมูลเวลาที่แน่นอน ค่าqที่สูงขึ้นบ่งบอกถึงการพึ่งพาเงื่อนไขข้อผิดพลาดในอดีตที่แข็งแกร่งกว่าเพื่อทําการคาดการณ์
พารามิเตอร์คําสั่งซื้อตามฤดูกาล:
-
P: ลําดับตามฤดูกาลของคอมโพเนนต์ AR คล้ายกับpแต่สําหรับส่วนตามฤดูกาล -
D: ลําดับตามฤดูกาลของความแตกต่างคล้ายกับdแต่สําหรับส่วนตามฤดูกาล -
Q: ลําดับตามฤดูกาลของส่วนประกอบ MA คล้ายกับqแต่สําหรับส่วนตามฤดูกาล -
s: จํานวนขั้นตอนเวลาต่อรอบตามฤดูกาล (ตัวอย่างเช่น 12 สําหรับข้อมูลรายเดือนที่มีกาลรายปี)
# Hyperparameter tuning
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
print('Examples of parameter combinations for Seasonal ARIMA...')
print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[1]))
print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[2]))
print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[3]))
print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[4]))
SARIMAX มีพารามิเตอร์อื่น ๆ:
enforce_stationarity: แบบจําลองควรบังคับใช้สเตชันนาริตี้ในข้อมูลอนุกรมเวลาก่อนที่จะพอดีกับแบบจําลอง SARIMAX หรือไม่ถ้า
enforce_stationarityถูกตั้งค่าเป็นTrue(ค่าเริ่มต้น) จะระบุว่าแบบจําลอง SARIMAX ควรบังคับใช้สเตชันนารีในข้อมูลอนุกรมเวลา จากนั้นแบบจําลอง SARIMAX จะใช้ความแตกต่างกับข้อมูลโดยอัตโนมัติเพื่อทําให้เป็นแบบนิ่งตามที่ระบุโดยคําสั่งdและDก่อนที่จะปรับแบบจําลองให้เหมาะสม นี่เป็นแนวทางปฏิบัติทั่วไปเนื่องจากแบบจําลองชุดข้อมูลเวลาจํานวนมากรวมถึง SARIMAX สันนิษฐานว่าข้อมูลเป็นแบบอยู่กับที่สําหรับชุดข้อมูลเวลาทั่วไป (ตัวอย่างเช่นมีแนวโน้มหรือกาล) เป็นแนวทางปฏิบัติที่ดีในการตั้งค่า
enforce_stationarityเป็นTrueและให้แบบจําลอง SARIMAX จัดการกับความแตกต่างเพื่อให้เกิดความแน่นอน สําหรับชุดข้อมูลเวลาแบบประจําเครื่อง (ตัวอย่างเช่น ชุดข้อมูลที่ไม่มีแนวโน้มหรือฤดูกาล) ให้ตั้งค่าenforce_stationarityเป็นFalseเพื่อหลีกเลี่ยงความแตกต่างที่ไม่จําเป็นenforce_invertibility: ควบคุมว่าแบบจําลองควรบังคับใช้ความผกผันกับพารามิเตอร์ที่ประเมินในระหว่างกระบวนการปรับให้เหมาะสมหรือไม่ถ้า
enforce_invertibilityถูกตั้งค่าเป็นTrue(ค่าเริ่มต้น) แสดงว่าแบบจําลอง SARIMAX ควรบังคับใช้ความผกผันบนพารามิเตอร์โดยประมาณ ความสามารถในการสลับเปลี่ยนเพื่อให้แน่ใจว่าแบบจําลองได้รับการกําหนดไว้อย่างดีและสัมประสิทธิ์ AR และ MA โดยประมาณนั้นอยู่ภายในช่วงของสเตชันนาติการบังคับใช้ความสามารถในการแสดงแทนตัวช่วยให้แน่ใจว่าแบบจําลอง SARIMAX เป็นไปตามข้อกําหนดทางทฤษฎีสําหรับแบบจําลองชุดข้อมูลเวลาที่เสถียร นอกจากนี้ยังช่วยป้องกันปัญหาเกี่ยวกับการประมาณค่าแบบจําลองและความเสถียร
ค่าเริ่มต้นคือแบบจําลอง AR(1) ซึ่งจะอ้างอิงถึง (1, 0, 0) อย่างไรก็ตาม เป็นการทั่วไปที่จะลองการรวมกันของพารามิเตอร์คําสั่งซื้อและพารามิเตอร์คําสั่งซื้อตามฤดูกาลที่แตกต่างกัน และประเมินประสิทธิภาพของแบบจําลองสําหรับชุดข้อมูล ค่าที่เหมาะสมอาจแตกต่างจากชุดข้อมูลหนึ่งไปยังอีกชุดข้อมูลหนึ่ง
การกําหนดค่าที่เหมาะสมที่สุดมักจะเกี่ยวข้องกับการวิเคราะห์ฟังก์ชัน autocorrelation (ACF) และฟังก์ชันความสัมพันธ์อัตโนมัติบางส่วน (PACF) ของข้อมูลอนุกรมเวลา ซึ่งมักจะเกี่ยวข้องกับการใช้เกณฑ์การเลือกแบบจําลอง - ตัวอย่างเช่น เกณฑ์ข้อมูลที่เรียกกันว่า (AIC) หรือเกณฑ์ข้อมูล Bayesian (BIC)
ปรับแต่งค่า hyperparameters:
# Tune the hyperparameters to determine the best model
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(y,
order=param,
seasonal_order=param_seasonal,
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit(disp=False)
print('ARIMA{}x{}12 - AIC:{}'.format(param, param_seasonal, results.aic))
except:
continue
หลังจากการประเมินผลลัพธ์ก่อนหน้า คุณสามารถกําหนดค่าสําหรับทั้งพารามิเตอร์คําสั่งซื้อและพารามิเตอร์คําสั่งซื้อตามฤดูกาลได้ ตัวเลือกคือ order=(0, 1, 1) และ seasonal_order=(0, 1, 1, 12)ซึ่งเสนอ AIC ต่ําสุด (ตัวอย่างเช่น 279.58) ใช้ค่าเหล่านี้เพื่อฝึกแบบจําลอง
ฝึกแบบจําลอง
# Model training
mod = sm.tsa.statespace.SARIMAX(y,
order=(0, 1, 1),
seasonal_order=(0, 1, 1, 12),
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit(disp=False)
print(results.summary().tables[1])
รหัสนี้แสดงภาพการคาดการณ์ชุดข้อมูลเวลาสําหรับข้อมูลการขายเฟอร์นิเจอร์ ผลลัพธ์การลงจุดจะแสดงทั้งข้อมูลที่สังเกตการณ์และการคาดการณ์ล่วงหน้าหนึ่งขั้นตอน โดยมีพื้นที่แรเงาสําหรับช่วงความเชื่อมั่น
# Plot the forecasting results
pred = results.get_prediction(start=maximim_date, end=maximim_date+pd.DateOffset(months=6), dynamic=False) # Forecast for the next 6 months (months=6)
pred_ci = pred.conf_int() # Extract the confidence intervals for the predictions
ax = y['2019':].plot(label='observed')
pred.predicted_mean.plot(ax=ax, label='One-step ahead forecast', alpha=.7, figsize=(12, 7))
ax.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], color='k', alpha=.2)
ax.set_xlabel('Date')
ax.set_ylabel('Furniture Sales')
plt.legend()
plt.show()
# Validate the forecasted result
predictions = results.get_prediction(start=maximim_date-pd.DateOffset(months=6-1), dynamic=False)
# Forecast on the unseen future data
predictions_future = results.get_prediction(start=maximim_date+ pd.DateOffset(months=1),end=maximim_date+ pd.DateOffset(months=6),dynamic=False)
ใช้ predictions เพื่อประเมินประสิทธิภาพของแบบจําลอง โดยเปรียบเทียบกับค่าจริง ค่า predictions_future บ่งชี้การคาดการณ์ในอนาคต
# Log the model and parameters
model_name = f"{EXPERIMENT_NAME}-Sarimax"
with mlflow.start_run(run_name="Sarimax") as run:
mlflow.statsmodels.log_model(results,model_name,registered_model_name=model_name)
mlflow.log_params({"order":(0,1,1),"seasonal_order":(0, 1, 1, 12),'enforce_stationarity':False,'enforce_invertibility':False})
model_uri = f"runs:/{run.info.run_id}/{model_name}"
print("Model saved in run %s" % run.info.run_id)
print(f"Model URI: {model_uri}")
mlflow.end_run()
# Load the saved model
loaded_model = mlflow.statsmodels.load_model(model_uri)
ขั้นตอนที่ 4: ให้คะแนนแบบจําลองและบันทึกการคาดการณ์
รวมค่าจริงเข้ากับค่าที่คาดการณ์ไว้เพื่อสร้างรายงาน Power BI จัดเก็บผลลัพธ์เหล่านี้ไว้ในตารางภายในเลคเฮ้าส์
# Data preparation for Power BI visualization
Future = pd.DataFrame(predictions_future.predicted_mean).reset_index()
Future.columns = ['Date','Forecasted_Sales']
Future['Actual_Sales'] = np.NAN
Actual = pd.DataFrame(predictions.predicted_mean).reset_index()
Actual.columns = ['Date','Forecasted_Sales']
y_truth = y['2023-02-01':]
Actual['Actual_Sales'] = y_truth.values
final_data = pd.concat([Actual,Future])
# Calculate the mean absolute percentage error (MAPE) between 'Actual_Sales' and 'Forecasted_Sales'
final_data['MAPE'] = mean_absolute_percentage_error(Actual['Actual_Sales'], Actual['Forecasted_Sales']) * 100
final_data['Category'] = "Furniture"
final_data[final_data['Actual_Sales'].isnull()]
input_df = y.reset_index()
input_df.rename(columns = {'Order Date':'Date','Sales':'Actual_Sales'}, inplace=True)
input_df['Category'] = 'Furniture'
input_df['MAPE'] = np.NAN
input_df['Forecasted_Sales'] = np.NAN
# Write back the results into the lakehouse
final_data_2 = pd.concat([input_df,final_data[final_data['Actual_Sales'].isnull()]])
table_name = "Demand_Forecast_New_1"
spark.createDataFrame(final_data_2).write.mode("overwrite").format("delta").save(f"Tables/{table_name}")
print(f"Spark DataFrame saved to delta table: {table_name}")
ขั้นตอนที่ 5: แสดงภาพใน Power BI
รายงาน Power BI แสดงข้อผิดพลาดเปอร์เซ็นต์แบบสัมบูรณ์ (MAPE) ค่าเฉลี่ยของ 16.58 เมตริก MAPE กําหนดความแม่นยําของวิธีการคาดการณ์ ซึ่งแสดงถึงความแม่นยําของปริมาณที่คาดการณ์เมื่อเปรียบเทียบกับปริมาณจริง
MAPE เป็นเมตริกที่ตรงไปตรงมา MAPE 10% แสดงว่าค่าเบี่ยงเบนเฉลี่ยระหว่างค่าที่คาดการณ์และค่าจริงคือ 10%โดยไม่คํานึงว่าค่าเบี่ยงเบนเป็นบวกหรือค่าลบ มาตรฐานของค่า MAPE ที่น่าปรารถนาแตกต่างกันไปในแต่ละอุตสาหกรรม
เส้นสีน้ําเงินอ่อนในกราฟนี้แสดงถึงค่ายอดขายจริง เส้นสีน้ําเงินเข้มแสดงถึงค่ายอดขายที่คาดการณ์ไว้ การเปรียบเทียบยอดขายจริงและยอดขายที่คาดการณ์ไว้แสดงให้เห็นว่าแบบจําลองทํานายยอดขายสําหรับหมวดหมู่ Furniture ได้อย่างมีประสิทธิภาพในช่วงหกเดือนแรกของปี 2023
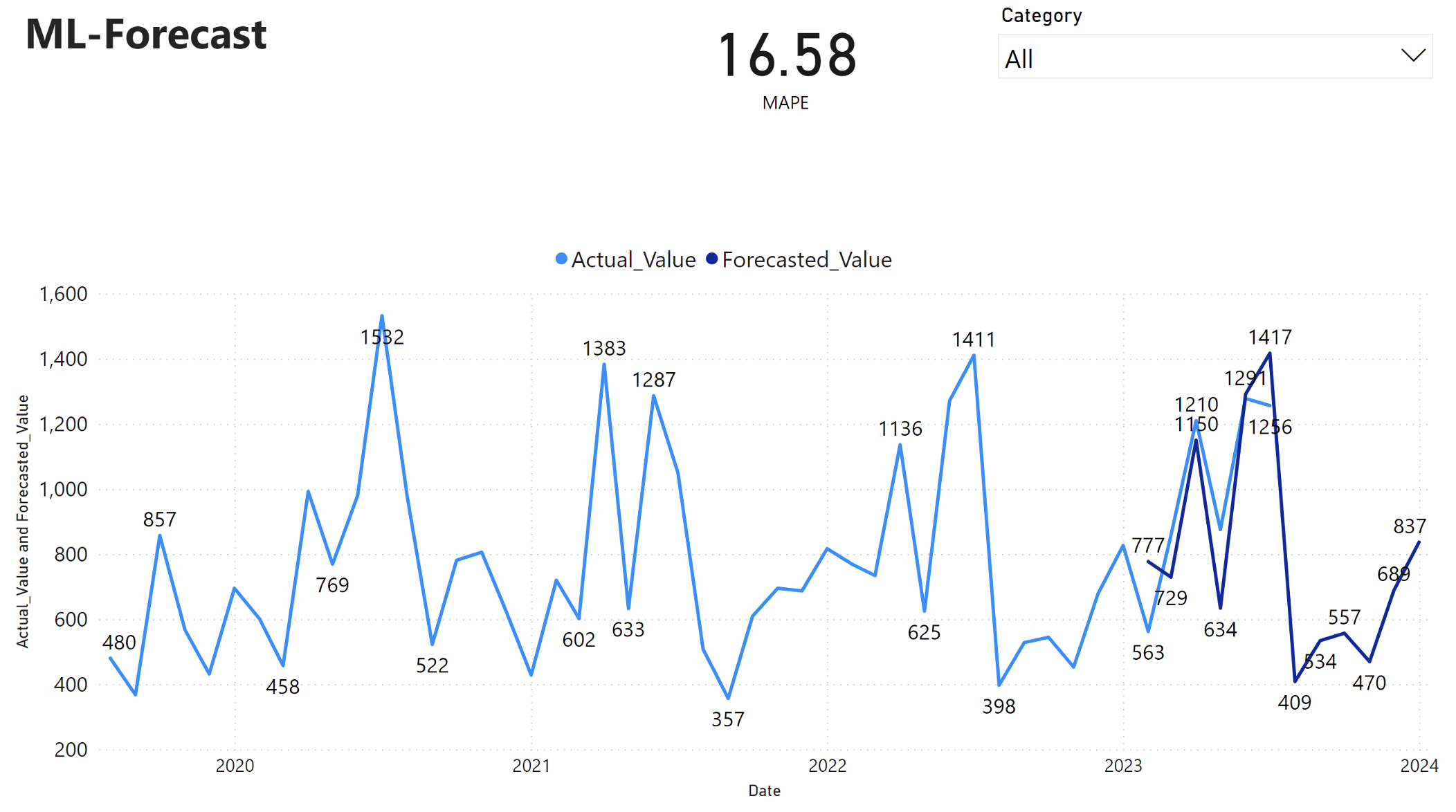
จากการสังเกตการณ์นี้ เราสามารถมั่นใจในความสามารถในการคาดการณ์ของแบบจําลอง สําหรับยอดขายโดยรวมในหกเดือนที่ผ่านมาของปี 2023 และขยายเป็น 2024 ความเชื่อมั่นนี้สามารถให้ข้อมูลการตัดสินใจเชิงกลยุทธ์เกี่ยวกับการจัดการสินค้าคงคลัง การจัดซื้อวัตถุดิบ และข้อควรพิจารณาที่เกี่ยวข้องกับธุรกิจอื่น ๆ
เนื้อหาที่เกี่ยวข้อง
- วิธีใช้สมุดบันทึก Microsoft Fabric
- แบบจําลองการเรียนรู้ของเครื่อง ใน Microsoft Fabric
- แบบจําลองการเรียนรู้ของเครื่อง Train
- การทดลองการเรียนรู้ของเครื่อง ใน Microsoft Fabric