Testhypotes med t-test
Viktigt
Stödet för Machine Learning Studio (klassisk) upphör den 31 augusti 2024. Vi rekommenderar att du byter till Azure Machine Learning innan dess.
Från och med den 1 december 2021 kan du inte längre skapa nya Machine Learning Studio-resurser (klassisk). Du kan fortsätta att använda befintliga Machine Learning Studio-resurser (klassisk) till och med den 31 augusti 2024.
- Se information om hur du flyttar maskininlärningsprojekt från ML Studio (klassisk) till Azure Machine Learning.
- Läs mer om Azure Machine Learning.
Dokumentationen om ML Studio (klassisk) håller på att dras tillbaka och kanske inte uppdateras i framtiden.
Jämför medelvärden från två kolumner med hjälp av ett t-test
Kategori: Statistiska funktioner
Anteckning
Gäller endast för: Machine Learning Studio (klassisk)
Liknande dra och släpp-moduler finns i Azure Machine Learning designer.
Modulöversikt
Den här artikeln beskriver hur du använder testhypotesen Med t-Test-modulen i Machine Learning Studio (klassisk) för att generera poäng för tre typer av t-tester:
- T-test med enkla exempel
- Parat t-test
- Obetalt t-test
I allmänhet hjälper ett t-test dig att jämföra om två grupper har olika medel. Anta till exempel att du utvärderar studiedata för patienter som fick läkemedels-A jämfört med patienter som fick läkemedel B, och du måste jämföra ett mått för återställningsfrekvensen för båda grupperna. Nollhypotesen förutsätter att återställningsfrekvensen är densamma i båda grupperna, och dessutom att värdena för återställningsfrekvensen har en normal fördelning i båda två grupperna.
Genom att använda testhypotes med t-Test och ange kolumnerna som innehåller återställningshastigheter som indata kan du få poäng som anger om skillnaden är meningsfull, vilket skulle innebära att nollhypotesen ska avvisas. Testet tar hänsyn till faktorer som hur stor skillnaden är mellan värdena, storleken på urvalet (större är bättre) och hur stor standardavvikelsen är (lägre är bättre).
Genom att granska resultaten av testhypotesen med hjälp av t-Test-modulen kan du avgöra om nollhypotesen är TRUE eller FALSE och granska förtroendepoängen (P) från t-testet.
Så här väljer du ett t-test
Välj ett exempel på ett t-test när dessa villkor gäller:
Du har ett enda urval av poäng.
Alla poäng är oberoende av varandra.
Samplingsfördelningen för xˉ är normal.
I allmänhet används t-test med ett enda exempel för att jämföra ett genomsnittligt värde med ett känt tal.
Välj ett parkopplat t-test när dessa villkor gäller:
Du har ett matchningspar med poäng. Du kan till exempel ha två olika mått per person eller matchade par av individer (till exempel en man och hustru).
Varje poängpar är oberoende av vartannat par.
Samplingsfördelningen av d är normal.
Ett parkopplat t-test är användbart när du jämför relaterade fall. Genom att medelvärdet av skillnaderna mellan poängen för de kopplade fallen kan du avgöra om den totala skillnaden är statistiskt signifikant.
Välj ett obetalt t-test när dessa villkor gäller:
Du har två oberoende resultatexempel. Det vill säger att det inte finns någon grund för att parkoppla poäng i exempel 1 med dem i exempel 2.
Alla poäng i ett exempel är oberoende av alla andra poäng i exemplet.
Samplingsfördelningen för x1- x2 är normal.
Alternativt kan du uppfylla kravet att variansen mellan grupperna är ungefär lika stor.
Så här konfigurerar du testhypotes med t-test
Använd en enda datauppsättning som indata. Kolumnerna som du jämför måste finnas i samma datauppsättning.
Om du behöver jämföra kolumner från olika datauppsättningar kan du isolera varje kolumn att jämföra med hjälp av Välj kolumner i datauppsättning och sedan sammanfoga dem till en datauppsättning med hjälp av Lägg till kolumner.
Lägg till testhypotesen med hjälp av t-Test-modulen i experimentet.
Du hittar den här modulen i kategorin Statistiska funktioner i Studio (klassisk).
Lägg till den datauppsättning som innehåller kolumnen eller kolumnerna som du vill analysera.
Bestäm vilken typ av t-test som är lämplig för dina data. Se Så här väljer du ett t-test.
Enkelt exempel: Om du använder ett enda exempel anger du följande parametrar:
Null-hypotes μ: Ange det värde som ska användas som null-hypotesiserat medelvärde för exemplet. Detta anger det förväntade medelvärdet som exempelvärdet ska testas mot.
Målkolumn: Använd kolumnväljaren för att välja en enda numerisk kolumn för testning.
Hypotestyp: Välj ett enstjärts- eller tvåstjärtstest. Standardvärdet är ett tvåsidigt test. Det här är den vanligaste typen av test, där den förväntade fördelningen är symmetrisk runt noll.
Alternativet One Tail GT är ett enkelsidigt alternativ som är större än testet. Det här testet ger mer kraft för att identifiera en effekt i en riktning, genom att inte testa effekten i den andra riktningen.
Alternativet One Tail LT ger ett enkelsidigt mindre än test.
α: Ange en konfidensfaktor. Det här värdet används för att utvärdera värdet för P (modulens första utdata). Om p är lägre än konfidensfaktorn avvisas nollhypotesen.
PairedSamples: Om du jämför två exempel från samma population anger du följande parametrar:
Null-hypotes μ: Ange ett värde som representerar exempelskillnaden mellan exempelparet.
Målkolumn: Använd kolumnväljaren för att välja de två numeriska kolumnerna som ska testas.
Hypotestyp: Välj antingen ett enstjärts- eller tvåstjärtstest. Standardvärdet är ett tvåsidigt test.
α: Ange konfidensfaktorn. Det här värdet används för att utvärdera värdet för P (modulens första utdata)> Om p är lägre än konfidensfaktorn avvisas nollhypotesen.
UnpairedSamples: Om du jämför två omdefinierade exempel anger du följande parametrar:
- Anta lika varians: Avmarkera det här alternativet när exemplen kommer från olika populationer.
- Null-hypotes μ1: Ange medelvärdet för den första kolumnen.
- Null-hypotes μ2: Ange medelvärdet för den andra kolumnen.
- Målkolumner: Använd kolumnväljaren för att välja två numeriska kolumner att testa.
- Hypotestyp: Ange om testet är enstjärt eller tvåstjärt. Standardvärdet är ett tvåsidigt test.
- α: Ange konfidensfaktorn. Det här värdet används för att utvärdera värdet för P (modulens första utdata)> Om p är lägre än konfidensfaktorn avvisas nollhypotesen.
Kör experimentet.
Resultat
Utdata från modulen är en datauppsättning som innehåller t-testresultaten och en transformering som du kan spara om du vill för att tillämpa på den här eller en annan datauppsättning med hjälp av Tillämpa transformering.
Datamängden med poäng innehåller dessa värden, oavsett vilken typ av t-test du använde:
- En sannolikhetspoäng som anger konfidensen för nollhypotesen
- Ett värde som anger om nollhypotesen ska avvisas
Tips
Kom ihåg att målet är att avgöra om du kan avvisa nollhypotesen. Poängen 0 innebär inte att du bör acceptera nollhypotesen: det innebär att du inte har tillräckligt med data och behöver undersökas ytterligare.
Tekniska anteckningar
Modulen namnger automatiskt utdatakolumnerna enligt följande konventioner, beroende på vilken typ av t-test som valdes och om resultatet var att avvisa eller acceptera nollhypotesen.
Med angivna indatakolumner med namn {0} och {1}skapar modulen följande namn:
| Kolumner | SingleSampleSet | PairedSamples | UnpairedSamples |
|---|---|---|---|
| Utdatakolumn P | P_ss({0}) | P_ps({0}, {1}) | P_us({0}, {1}) |
| Utdatakolumnen RejectH0 | RejectH0_ss({0})" | RejectH0_ps({0}, {1}) | RejectH0_us({0}, {1}) |
Hur poäng beräknas
Den här modulen beräknar och använder exempelstandardavvikelsen. därför används (n-1) ekvationen i nämnaren.
Beräkningspoäng för ett test med ett enda exempel
Med tanke på ett enskilt urval av poäng, alla oberoende av varandra och en normal fördelning, beräknas poängen på följande sätt:
Ta följande indata:
- En enda kolumn med värden från datauppsättningen
- Parametern nollhypotes (H0) μ0
- Konfidenspoängen som anges av α
Extrahera antalet exempel (n).
Beräkna medelvärdet av exempeldata.
Beräkna standardavvikelsen (s) för exempeldata.
Beräkna t och frihetsgrader (df):
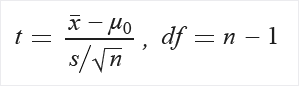
Extrahera sannolikhet P från distributionstabellen T med hjälp av t och df.
Beräkningspoäng för ett parkopplat t-test
Med tanke på en matchad uppsättning poäng, där varje par är oberoende av det andra och en normal fördelning i varje uppsättning, beräknas poängen på följande sätt:
Ta följande indata:
- Två kolumner med värden från datauppsättningen
- Parametern nullhypotes (H0) d0
- Konfidenspoängen som anges av α
Extrahera ett visst antal exempelpar (n).
Beräkna medelvärdet av skillnader för exempeldata:
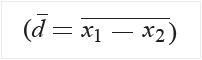
Beräkna standardavvikelsen för skillnader (sd).
Beräkna t och frihetsgrader (df):
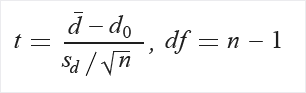
Extrahera sannolikhet (P) från distributionstabellen (T) med hjälp av t och df.
Beräkningspoäng för ett obetalt t-test
Med tanke på två oberoende urval av poäng, med en normal fördelning av värden i varje exempel, beräknas poängen på följande sätt:
Ta följande indata:
- En datauppsättning som innehåller två kolumner med
doubles - Parametern nollhypotes (H0) (d0)
- Konfidenspoängen som anges av α
- En datauppsättning som innehåller två kolumner med
Extrahera ett antal exempel i varje grupp, n1 och n2.
Beräkna medelvärdena för var och en av exempeluppsättningarna.
Beräkna standardavvikelsen för varje grupp som s1 och s2.
Beräkna t och frihetsgrader (df):
Alternativt kan du uppfylla kravet på att variansen mellan grupperna är ungefär lika stor, enligt följande:
Beräkna den poolade standardavvikelsen först:
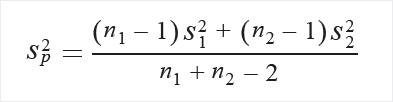
Om det inte finns något antagande om variansjämlikhet beräknar du på följande sätt:
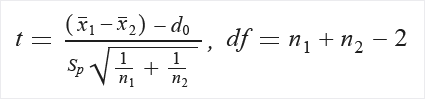
Extrahera P från distributionstabellen (T) med hjälp av t och df.
Beräkna nollhypotesen
Sannolikheten för nollhypotesen, som betecknas som P, beräknas på följande sätt:
Om P < α anger du flaggan Avvisa till Sant.
Om P ≥ α anger du flaggan Avvisa till Falskt.
Förväntade indata
| Namn | Typ | Description |
|---|---|---|
| Datamängd | Datatabell | Indatauppsättning |
Modulparametrar
| Name | Intervall | Typ | Standardvärde | Description |
|---|---|---|---|---|
| Hypotestyp | Valfri | Hypotesen | Tvåstjärt | Elevens t-test nollhypotestyp |
| Null-hypotes μ | Valfri | Float | 0.0 | För T-test med ett enda exempel är det null-hypotesiserade medelvärdet för exemplet För det kopplade t-testet är exempelskillnaden |
| Målkolumner | Valfri | ColumnSelection | Ingen | Markeringsmönster för målkolumner |
| Anta lika varianser | Valfri | Boolesk | Sant | Anta att varianserna för två exempel är lika med Gäller endast för obetalda exempel |
| Null-hypotes μ1 | Valfri | Float | 0.0 | Null-hypotesiserat medelvärde för det första exemplet |
| Α | [0.0;1.0] | Float | 0,95 | Konfidensfaktor (om P är lägre än konfidensfaktorn avvisas nollhypotesen) |
Utdata
| Namn | Typ | Description |
|---|---|---|
| P | Datatabell | En sannolikhetspoäng som anger konfidensen för nollhypotesen |
| Avvisa H0 | Datatabell | Värde som anger om nollhypotesen ska avvisas |
Undantag
| Undantag | Description |
|---|---|
| Fel 0003 | Ett undantag inträffar om en eller flera indata är null eller tomma. |
| Fel 0008 | Ett undantag inträffar om parametern inte ligger inom intervallet. |
| Fel 0017 | Ett undantag inträffar om en eller flera angivna kolumner har en typ som inte stöds av den aktuella modulen. |
| Fel 0020 | Ett undantag inträffar om antalet kolumner i vissa datauppsättningar som skickas till modulen är för litet. |
| Fel 0021 | Ett undantag inträffar om antalet rader i vissa datauppsättningar som skickas till modulen är för litet. |
| Fel 0031 | Ett undantag inträffar om antalet kolumner i kolumnuppsättningen är mindre än vad som behövs. |
| Fel 0032 | Ett undantag inträffar om argumentet inte är ett tal. |
| Fel 0033 | Ett undantag inträffar om argumentet är oändligt. |
En lista över fel som är specifika för Studio-moduler (klassiska) finns i Machine Learning Felkoder.
En lista över API-undantag finns i Machine Learning REST API-felkoder.