Utvärdera sannolikhetsfunktionen
Viktigt
Stödet för Machine Learning Studio (klassisk) upphör den 31 augusti 2024. Vi rekommenderar att du byter till Azure Machine Learning innan dess.
Från och med den 1 december 2021 kan du inte längre skapa nya Machine Learning Studio-resurser (klassisk). Du kan fortsätta att använda befintliga Machine Learning Studio-resurser (klassisk) till och med den 31 augusti 2024.
- Se information om hur du flyttar maskininlärningsprojekt från ML Studio (klassisk) till Azure Machine Learning.
- Läs mer om Azure Machine Learning.
Dokumentationen om ML Studio (klassisk) håller på att dras tillbaka och kanske inte uppdateras i framtiden.
Passar en angiven sannolikhetsfördelningsfunktion till en datauppsättning
Kategori: Statistiska funktioner
Anteckning
Gäller endast för: Machine Learning Studio (klassisk)
Liknande dra och släpp-moduler finns i Azure Machine Learning designer.
Modulöversikt
Den här artikeln beskriver hur du använder modulen Utvärdera sannolikhetsfunktion i Machine Learning Studio (klassisk) för att beräkna statistiska mått som beskriver en kolumns fördelning, till exempel Bernoulli-, Pareto- eller Poisson-distributionerna.
Om du vill använda den här modellen ansluter du en datauppsättning som innehåller minst en kolumn med numeriska värden och väljer en sannolikhetsfördelning att testa. Modulen returnerar en datatabell som innehåller värden från den angivna sannolikhetsfunktionen.
Du kan beräkna något av dessa värden för den valda sannolikhetsfördelningen:
- kumulativ distributionsfunktion (cdf)
- invertera kumulativ fördelningsfunktion (InverseCdf)
- sannolikhetsdensitetsfunktion (Pdf)
Varför är sannolikhetsfördelningen användbar?
När du utvärderar dina data mot en sannolikhetsfördelning mappar du kolumnvärden mot en uppsättning värden med kända egenskaper. Genom att veta om dina data motsvarar en av dessa välkända distributioner kanske du kan härleda andra egenskaper för dina data. I allmänhet kan du få bättre förutsägelser från en modell när du kan identifiera den distribution som passar bäst för data.
Frågan om vilken sannolikhetsfördelningsfunktion som ska användas beror på vilka data och variabler som mäts. Vissa fördelningar är till exempel utformade för att beskriva sannolikheter för diskreta värden. andra är endast avsedda för användning med kontinuerliga numeriska variabler. För vissa fördelningar måste du också veta i förväg ett förväntat medelvärde, frihetsgrader och så vidare. Mer information finns i Sannolikhetsfördelningar som stöds
Så här konfigurerar du funktionen Utvärdera sannolikhet
Alla alternativ ändras beroende på vilken typ av sannolikhetsfördelning du vill beräkna. Om du ändrar sannolikhetsfördelningsmetoden återställs andra val som du kan ha gjort.
Se därför till att välja alternativet Distribution först!
Den datauppsättning som används som indata ska innehålla numeriska data. Andra typer av data ignoreras.
För varje analys kan du använda en enda sannolikhetsfördelningsmetod. Om du vill beräkna en annan sannolikhetsfördelning lägger du till en separat instans av modulen för varje distribution som du tänker testa.
Lägg till modulen Utvärdera sannolikhetsfunktion i experimentet. Du hittar den här modulen i kategorin Statistiska funktioner i Machine Learning Studio (klassisk).
Anslut en datauppsättning som innehåller minst en kolumn med tal.
Använd alternativet Distribution för att välja den typ av sannolikhetsfördelning som du vill beräkna. Se Sannolikhetsfördelningar som stöds för en lista över alternativ och deras argument.
Ange alla parametrar som krävs av fördelningen.
Välj en av tre statistik att skapa: den kumulativa fördelningsfunktionen (cdf), den inverterade kumulativa distributionsfunktionen (InverseCdf) eller funktionen Sannolikhetsdensitet (pdf).
Se avsnittet Tekniska anteckningar för definitioner.
Använd kolumnväljaren för att välja vilka kolumner som den valda sannolikhetsfördelningen ska beräknas för.
Alla kolumner som du väljer måste ha en numerisk datatyp.
Dataområdet i kolumnen måste också vara giltigt med tanke på den valda sannolikhetsfunktionen. Annars kan ett fel eller ett NaN-resultat inträffa.
För glesa kolumner bearbetas inte alla värden som motsvarar bakgrunds nollor.
Använd alternativet Resultatläge för att ange hur resultatet ska matas ut. Du kan ersätta kolumnvärden med sannolikhetsfördelningsvärdena, lägga till de nya värdena i datauppsättningen eller bara returnera sannolikhetsfördelningsvärdena.
Kör experimentet eller högerklicka på modulen Utvärdera sannolikhetsfunktion och klicka på Kör valt.
Resultat
Följande tabell innehåller ett exempel på resultat, med hjälp av alternativet Lägg till , i en kolumn med en enda temperatur från exempeldatauppsättningen Forest Fires .
| temp | StandardNormal.Cdf(temp) | StandardNormal.Pdf(temp) | FFisher.cdf(temp | FFisher.cdf(temp |
|---|---|---|---|---|
| 8.2 | 1 | 1 | 0.984774 | 0.004349 |
| 18 | 1 | 1 | 0.997896 | 0.000311 |
| 14.6 | 1 | 1 | 0.996352 | 0.000648 |
| 8.3 | 1 | 1 | 0.985201 | 0.004187 |
| 11,4 | 1 | 1 | 0.993147 | 0.001502 |
Rubrikerna för de genererade kolumnerna innehåller sannolikhetsfördelningen som användes.
Om du inte är säker på vilken sannolikhetsfördelning som sannolikt passar dina data kan du skapa ett snabbt diagram med kumulativ fördelning och sannolikhetstäthet för valfri numerisk kolumn.
- Högerklicka på datauppsättningen eller modulens utdata och välj Visualisera.
- Välj kolumnen av intresse och välj kumulativ fördelning eller sannolikhetstäthet i histogramfönstret.
- Ett diagram över fördelningen, som följande, läggs ovanpå histogrammet som representerar data.
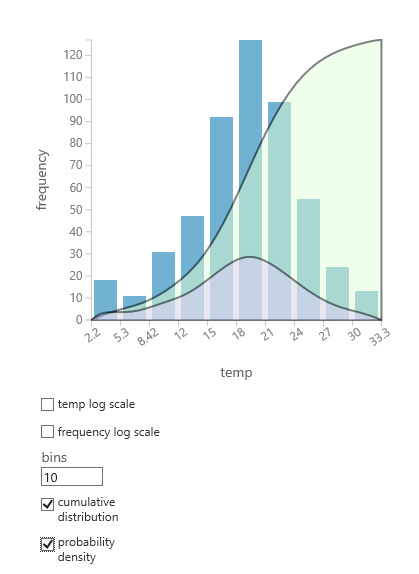
Sannolikhetsfördelningar som stöds
Modulen Utvärdera sannolikhetsfunktion stöder följande fördelningar:
Bernoulli
Bernoulli-fördelningen är en fördelning över binära värden: med andra ord modellerar den förväntade fördelningen när endast två värden är möjliga.
Om du vill beräkna väljer du Bernoulli och anger följande alternativ:
- Sannolikheten för att lyckas
Parametern p anger sannolikheten för att en 1 genereras. Ange ett tal (float) mellan 0,0 och 1,0 som anger sannolikheten för att lyckas. Standardvärdet är 0,5.
Beta
Betadistributionen är en kontinuerlig univariate-distribution.
Om du vill beräkna väljer du Beta och anger följande alternativ:
Form
Ange ett värde för att ändra formen på fördelningen.En formparameter är en parameter för en sannolikhetsfördelning som inte definierar dess plats eller skala. När du anger ett värde för formen ändrar parametern därför formen på fördelningen i stället för att flytta, sträcka ut eller krympa den.
Värdet måste vara ett tal (
double). Standardvärdet är 1.0.Skalning
Ange ett tal som ska användas för att skala fördelningen.Genom att tillämpa ett skalningsvärde på fördelningen kan du krympa eller sträcka ut det.
Standardvärdet är 1,0. Värdena måste vara positiva tal.
Övre gräns
Ange ett tal (double) som representerar den övre gränsen för fördelningen. Standardvärdet är 1.0.Nedre gräns
Ange ett tal (double) som representerar den nedre gränsen för fördelningen. Standardvärdet är 0,0.
Binomial
Binomialfördelningen är en diskret univariate-distribution. Binomialfördelningen används för att modellera antalet lyckade resultat i ett exempel. Ersättning används vid sampling. För sampling utan ersättning använder du hypergeometrisk fördelning.
Om du vill beräkna väljer du Binomial och anger följande alternativ:
Sannolikheten att lyckas
Ange ett tal (float) mellan 0,0 och 1,0 som anger sannolikheten för att lyckas. Standardvärdet är 0,5.Antal utvärderingsversioner
Ange antalet utvärderingsversioner.Använd ett
integer, med ett minsta värde på 1. Standardvärdet är 3.
Cauchy
Kauchyfördelningen är en symmetrisk kontinuerlig sannolikhetsfördelning.
Om du vill beräkna väljer du Cauchy och anger följande alternativ:
Plats
Skriv ett tal (double) som representerar platsen för det 0:e elementet.Genom att ange ett värde för parametern Location kan du flytta sannolikhetsfördelningen uppåt eller nedåt i en numerisk skala.
Standardvärdet är 0,0.
ChiSquare
Chi2-fördelningen är en summa av kvadraterna av k oberoende, standard, normala, slumpmässiga variabler.
Om du vill beräkna väljer du ChiSquare och anger följande alternativ:
- Antal frihetsgrader Ange ett tal (
double) för att ange frihetsgrader. Standardvärdet är 1.0.
ChiSquareRightTailed
Det här alternativet ger en högersidig chi2-fördelning.
Om du vill beräkna väljer du ChiSquareRightTailed och anger följande alternativ:
- Antal frihetsgrader
Ange ett tal (double) för att ange frihetsgrader. Standardvärdet är 1.0.
Exponentiellt
Den exponentiella fördelningen är en fördelning över de verkliga talen som parametriseras med en icke-negativ parameter.
Om du vill beräkna väljer du Exponentiell och anger följande alternativ:
- Lambda
Ange ett tal (double) som ska användas som lambda-parameter. Standardvärdet är 1.0.
FFisher
Genererar sannolikheten för Fisher-statistiken för ett urval, även kallat Fisher F-fördelning. Den här fördelningen är tvåsidig.
Om du vill beräkna väljer du FFisher och anger följande alternativ:
Täljare frihetsgrader
Ange ett tal (double) för att ange de frihetsgrader som används i täljaren. Standardvärdet är 3.0.Frihetsgrader för nämnare
Ange ett tal (double) för att ange de frihetsgrader som används i nämnaren. Standardvärdet är 6.0.
FFisherRightTailed
Skapar en högersidig Fisher-distribution. Fisher-distributionen är också känd som Fisher F-distribution, Snedecor-distribution eller Fisher-Snedecor distribution. Den här specifika formen av fördelningen är högersidig.
Om du vill beräkna väljer du FFisherRightTailed och anger följande alternativ:
Täljare frihetsgrader
Ange ett tal (double) för att ange de frihetsgrader som används i täljaren. Standardvärdet är 3.0.Frihetsgrader för nämnare
Ange ett tal (double) för att ange de frihetsgrader som används i nämnaren. Standardvärdet är 6.0.
Gamma
Gammafördelningen är en familj av kontinuerliga sannolikhetsfördelningar med två parametrar. Chi-squared är till exempel ett specialfall för gammafördelningen.
Om du vill beräkna väljer du Gamma och anger följande alternativ:
Skalning
Ange ett värde som ska användas för att skala distributionen.Genom att tillämpa ett skalningsvärde på fördelningen kan du krympa eller sträcka ut det.
Standardvärdet är 1,0. Värdena måste vara positiva tal.
Plats
Skriv ett tal (double) som representerar platsen för det 0:e elementet.Genom att ange ett värde för parametern Location kan du flytta sannolikhetsfördelningen uppåt eller nedåt i en numerisk skala.
Standardvärdet är 0,0.
GeneralizedExtremeValues
Skapar en distribution som utvecklats för att hantera extrema värden. Den generaliserade extremvärdesfördelningen (GEV) är faktiskt en grupp med kontinuerliga sannolikhetsfördelningar som kombinerar Gumbel-, Fréchet- och Weibull-fördelningarna (även kallade extremfördelningar av typen I, II och III).
Mer information om extremvärdesteori finns i den här artikeln på Wikipedia: Fisher-Tippet-Gnedenko-teorem.
Om du vill beräkna väljer du GeneralizedExtremeValues och anger följande alternativ:
Form
Ange ett värde för att ändra formen på fördelningen.En formparameter är en parameter för en sannolikhetsfördelning som inte definierar dess plats eller skala. När du anger ett värde för formen ändrar parametern därför formen på fördelningen i stället för att flytta, sträcka ut eller krympa den.
Värdet måste vara ett tal (
double). Standardvärdet är 1.0.Skalning
Ange ett värde som ska användas för att skala distributionen.Genom att tillämpa ett skalningsvärde på fördelningen kan du krympa eller sträcka ut det.
Standardvärdet är 1,0. Värdena måste vara positiva tal.
Plats
Skriv ett tal (double) som representerar platsen för det 0:e elementet.Genom att skriva ett värde för parametern Location (Plats ) kan du flytta sannolikhetsfördelningen uppåt eller nedåt i en numerisk skala.
Standardvärdet är 0,0.
Geometriska
Den geometriska fördelningen är en fördelning över positiva heltal som parametriseras med ett positivt reellt tal.
Om du vill beräkna väljer du Geometrisk och anger följande alternativ:
- Sannolikheten att lyckas
Ange ett tal (float) mellan 0,0 och 1,0 som anger sannolikheten för att lyckas. Standardvärdet är 0,5.
Anteckning
Den här implementeringen av den geometriska fördelningen genererar inga nollor.
GumbelMax
Gumbel-fördelningen är en av flera extrema värdefördelningar. Alternativet GumbelMax implementerar fördelningen Maximal extrem värdetyp 1.
Om du vill beräkna väljer du GumbelMax och anger följande alternativ:
Skalning
Ange ett värde som ska användas för att skala distributionen.Genom att tillämpa ett skalningsvärde på fördelningen kan du krympa eller sträcka ut det.
Standardvärdet är 1,0. Värdena måste vara positiva tal.
Plats
Skriv ett tal (double) som representerar platsen för det 0:e elementet.Genom att skriva ett värde för parametern Location (Plats ) kan du flytta sannolikhetsfördelningen uppåt eller nedåt i en numerisk skala.
Standardvärdet är 0,0.
GumbelMin
Gumbel-fördelningen är en av flera extrema värdefördelningar. Gumbel-fördelningen kallas även för fördelningen minsta extrema värde (SEV) eller fördelningen minsta extrema värde (typ I). Alternativet GumbelMin implementerar fördelningen Minsta extrema värdetyp 1.
Om du vill beräkna väljer du GumbelMin och måste ange följande alternativ:
Skalning
Ange ett värde som ska användas för att skala distributionen.Genom att tillämpa ett skalningsvärde på fördelningen kan du krympa eller sträcka ut det.
Standardvärdet är 1,0. Värdena måste vara positiva tal.
Plats
Skriv ett tal (double) som representerar platsen för det 0:e elementet.Genom att skriva ett värde för parametern Location (Plats ) kan du flytta sannolikhetsfördelningen uppåt eller nedåt i en numerisk skala.
Standardvärdet är 0,0.
Hypergeometri
Den hypergeometriska fördelningen är en diskret sannolikhetsfördelning som beskriver antalet lyckade resultat i en sekvens med n-dragningar från en begränsad population utan ersättning, precis som binomialfördelningen beskriver antalet lyckade dragningar med ersättning.
Om du vill beräkna väljer du Hypergeometric och anger följande alternativ:
Number of samples
Skriv ett heltal som anger antalet exempel som ska användas. Standardvärdet är 9.Antal lyckade
Ange ett heltal som definierar värdet för lyckat resultat. Standardvärdet är 24.Befolkningsstorlek
Ange populationens storlek som ska användas när du beräknar den hypergeometriska fördelningen.
Laplace
Laplace-fördelningen är en fördelning över de verkliga talen, parametriserade med ett medelvärde och med en skalningsparameter.
Om du vill beräkna väljer du Laplace-distribution och anger följande alternativ:
Skalning
Ange ett värde som ska användas för att skala distributionen.Genom att tillämpa ett skalningsvärde på fördelningen kan du krympa eller sträcka ut det.
Standardvärdet är 1,0. Värdena måste vara positiva tal.
Plats
Skriv ett tal (double) som representerar platsen för det 0:e elementet.Genom att skriva ett värde för parametern Location (Plats ) kan du flytta sannolikhetsfördelningen uppåt eller nedåt i en numerisk skala.
Standardvärdet är 0,0.
Logistiska
Den logistiska distributionen liknar den normala fördelningen, men den har ingen gräns till vänster om fördelningen. Den logistiska distributionen används i logistisk regression och neurala nätverksmodeller och för modellering av biovetenskapliga data.
Om du vill beräkna väljer du Logistik och anger följande alternativ:
Skalning
Ange ett värde som ska användas för att skala distributionen.Genom att tillämpa ett skalningsvärde på fördelningen kan du krympa eller sträcka ut det.
Standardvärdet är 1,0. Värdena måste vara positiva tal.
Menar
Skriv ett tal (double)som anger det uppskattade medelvärdet för fördelningen. Standardvärdet är 0,0.
Lognormala
Den lognormala fördelningen är en kontinuerlig univariate-distribution.
Om du vill beräkna väljer du Lognormal och anger följande alternativ:
Menar
Ange ett tal (double) som anger det uppskattade medelvärdet för fördelningen. Standardvärdet är 0,0.Standardavvikelsen
Ange ett positivt tal (double) som anger den uppskattade standardavvikelsen för fördelningen. Standardvärdet är 1.0.
NegativeBinomial
Den negativa binomialfördelningen är en fördelning över de naturliga talen med två parametrar (r, p). I det specialfall som r är ett heltal kan du tolka fördelningen som antalet svansar före detförsta huvudet när sannolikheten för huvudet är p.
Om du vill beräkna väljer du NegativeBinomial och anger följande alternativ:
Sannolikheten att lyckas
Ange ett tal (float) mellan 0,0 och 1,0 som anger sannolikheten för att lyckas. Standardvärdet är 0,5.Antal lyckade
Skriv ett heltal som anger värdet för lyckat resultat. Standardvärdet är 24.
Normal
Den normala fördelningen kallas även gaussiska fördelningen.
Om du vill beräkna väljer du Normal och anger följande alternativ:
Menar
Ange ett tal (double) som anger det uppskattade medelvärdet för fördelningen. Standardvärdet är 0,0.Standardavvikelsen
Ange ett positivt tal (double) som anger den uppskattade standardavvikelsen för fördelningen. Standardvärdet är 1.0.
Pareto
Pareto-fördelningen är en sannolikhetsfördelning för power-law som sammanfaller med sociala, vetenskapliga, geofysiska, aktuariella och många andra typer av observerbara fenomen.
Om du vill beräkna väljer du Pareto och anger följande alternativ:
Form
Ange ett värde (valfritt) för att ändra formen på fördelningen.En formparameter är en parameter för en sannolikhetsfördelning som inte definierar dess plats eller skala. När du anger ett värde för formen ändrar parametern därför formen på fördelningen i stället för att flytta, sträcka ut eller krympa den.
Värdet måste vara ett tal (
double). Standardvärdet är 1.0.Skalning
Ange ett värde (valfritt) för att ändra distributionens skala. Genom att tillämpa ett skalningsvärde på fördelningen kan du krympa eller sträcka ut det.Värdet måste vara ett tal (
double). Standardvärdet är 1.0.
Poisson
I den här implementeringen används Knuths -metod för att generera Poisson-distribuerade slumpmässiga variabler. Mer information om Poisson-fördelningen finns i Poisson Regression.
Om du vill beräkna väljer du Poisson och anger följande alternativ:
- Menar
Ange ett tal (double) som anger det uppskattade medelvärdet för fördelningen. Standardvärdet är 0,0.
Rayleigh
Rayleigh-fördelningen är en kontinuerlig sannolikhetsfördelning. Som ett exempel på hur den uppstår kommer vindhastigheten att ha en Rayleigh-fördelning om komponenterna i den tvådimensionella vindhastighetsvektorn är okorrelerade och normalt fördelade med samma varians.
Om du vill beräkna väljer du Rayleigh och anger följande alternativ:
- Nedre gräns
Ange ett tal (double) som representerar den nedre gränsen för fördelningen. Standardvärdet är 0,0.
StandardNormal
Det här alternativet ger standardnormalfördelning, utan några andra parametrar.
Om du vill beräkna väljer du StandardNormal och väljer kolumnerna.
TStudent
Det här alternativet implementerar univariate Students t-distribution.
Om du vill beräkna väljer du TStudent och anger följande alternativ:
- Antal frihetsgrader
Ange ett tal (double) för att ange frihetsgrader. Standardvärdet är 1.0.
TStudentRightTailed
Implementerar univariate Students t-distribution med hjälp av en högerstjärt.
Om du vill beräkna väljer du TStudentRightTailed och anger följande alternativ:
- Antal frihetsgrader
Ange ett tal (double) för att ange frihetsgrader. Standardvärdet är 1.0.
TStudentTwoTailed
Implementerar en tvåsidig students t-distribution.
Om du vill beräkna väljer du TStudentTwoTailed och anger följande alternativ:
- Antal frihetsgrader
Ange ett tal (double) för att ange frihetsgrader. Standardvärdet är 1.0.
Enhetlig
Den enhetliga fördelningen kallas även för den rektangulära fördelningen.
Om du vill beräkna väljer du Enhetlig och anger följande alternativ:
Nedre gräns
Ange ett tal (double) som representerar den lägre gränsen för fördelningen. Standardvärdet är 0,0.Övre gräns
Ange ett tal (double) som representerar den övre gränsen för fördelningen. Standardvärdet är 1.0.
Weibull
Weibull-distributionen används ofta inom tillförlitlighetsteknik. Du kan använda dess Shape-parameter för att modellera många andra distributioner.
Om du vill beräkna väljer du Weibull och anger följande alternativ:
Form
Ange ett värde (valfritt) för att ändra formen på fördelningen.En formparameter är en parameter för en sannolikhetsfördelning som inte definierar dess plats eller skala. När du anger ett värde för formen ändrar parametern därför formen på fördelningen i stället för att flytta, sträcka ut eller krympa den.
Värdet måste vara ett tal (
double). Standardvärdet är 1.0.Skalning
Ange ett värde (valfritt) för att ändra distributionens skala. Genom att tillämpa ett skalningsvärde på fördelningen kan du krympa eller sträcka ut det.Värdet måste vara ett tal (
double). Standardvärdet är 1.0.
Tekniska anteckningar
Det här avsnittet innehåller implementeringsinformation, tips och svar på vanliga frågor.
Implementeringsdetaljer
Den här modulen stöder alla distributioner som finns i biblioteket öppen källkod MATH.NET Numeriska. Mer information finns i dokumentationen för biblioteket Math.Net.Numerics.Distribution .
Högersidiga och tvåsidiga distributioner visas som separata distributioner, inte som parametriserade versioner av basdistributioner. Det aktuella beteendet är att bevara kompatibiliteten med Excel.
Definitioner
Den här modulen stöder beräkning av något av dessa värden för den angivna distributionen:
cdf, eller den kumulativa fördelningsfunktionen
Returnerar sannolikheten för en sammansatt händelse, definierad som summan av ocurrences när den slumpmässiga variabeln tar ett värde som är mindre än ett visst värde x.
Med andra ord besvaras frågan: "Hur vanliga är exempel som är mindre än eller lika med det här värdet?"
Den här funktionen kan användas med både kontinuerliga och diskreta numeriska variabler.
InverseCdf eller den invertera kumulativa fördelningsfunktionen
Returnerar värdet som är associerat med ett specifikt kumulativt sannolikhetsvärde (cdf).
Med andra ord svarar den på frågan: "Vad är värdet för x där cdf-funktionen returnerar den kumulativa sannolikheten y?"
pdf eller sannolikhetsfunktionen
Beskriver den relativa sannolikheten för att en slumpmässig variabel ska vara ett specifikt värde.
Med andra ord svarar den på frågan: "Hur vanliga är prover med exakt det här värdet?"
Förväntade indata
| Namn | Typ | Description |
|---|---|---|
| Datamängd | Datatabell | Indatauppsättning |
Modulparametrar
| Name | Intervall | Typ | Standardvärde | Description |
|---|---|---|---|---|
| Distribution | Valfri | Sannolikhetsfördelning | StandardNormal | Välj den typ av sannolikhetsfördelning som ska genereras. |
| Metod | Valfri | ProbabilityDistributionMethod | Cdf | Välj den metod som ska användas vid beräkning av den valda sannolikhetsfördelningen. Alternativen är den kumulativa distributionsfunktionen (cdf), den inverterade kumulativa fördelningsfunktionen (InverseCdf) och sannolikhetsfunktionen eller massfunktionen (pdf). |
| Negativ binomial distributionsmetod | Valfri | ProbabilityDistributionMethodForNegativeBinomial | Cdf | Om du väljer den negativa binomialfördelningen anger du den metod som används för att utvärdera distributionen. |
| Sannolikheten för att lyckas | [0.0;1.0] | Float | 0,5 | Ange ett värde som ska användas som sannolikhet för att lyckas. |
| Form | Valfri | Float | 1.0 | Skriv ett värde som ändrar distributionens form. |
| Skala | >=0,0 | Float | 1.0 | Ange ett värde som ändrar skalan för fördelningen för att expandera eller krympa den i storlek. |
| Antal utvärderingsversioner | >=1 | Integer | 3 | Ange antalet utvärderingsversioner. |
| Nedre gräns | Valfri | Float | 0.0 | Ange ett tal som ska användas som den lägre gränsen för fördelningen |
| Övre gräns | Valfri | Float | 1.0 | Ange ett tal som ska användas som den övre gränsen för fördelningen |
| Location | Valfri | Float | 0.0 | Ange platsen för nollelementet i fördelningen. |
| Antal frihetsgrader | Valfri | Float | 1.0 | Ange antalet frihetsgrader. |
| Täljare frihetsgrader | Valfri | Float | 3.0 | Ange antalet frihetsgrader i täljaren. |
| Nämnare frihetsgrader | Valfri | Float | 6.0 | Ange antalet frihetsgrader i nämnaren. |
| Lambda | >=0,0 | Float | 1.0 | Ange ett värde för lambda-parametern. |
| Number of samples | Valfri | Integer | 9 | Ange antalet exempel. |
| Antal lyckade | Valfri | Integer | 24 | Ange ett värde som ska användas som antal lyckade. |
| Befolkningsstorlek | Valfri | Integer | 52 | Ange populationens storlek. |
| Medelvärde | Valfri | Float | 0.0 | Ange det uppskattade medelvärdet. |
| Standardavvikelse | >=0,0 | Float | 1.0 | Ange den uppskattade standardavvikelsen. |
| Kolumnuppsättning | Valfri | ColumnSelection | Välj de kolumner som sannolikhetsfördelningen ska beräknas för. | |
| Resultatläge | Valfri | OutputTo | ResultOnly | Ange hur resultaten ska sparas i utdatauppsättningen. Alternativen är att lägga till nya kolumner, ersätta befintliga kolumner eller endast mata ut resultatet. |
Utdata
| Namn | Typ | Description |
|---|---|---|
| Resultatdatauppsättning | Datatabell | Utdatauppsättning |
Undantag
En fullständig lista över felmeddelanden finns i Modulfelkoder.
| Undantag | Description |
|---|---|
| Fel 0017 | Ett undantag inträffar om en eller flera angivna kolumner har en typ som inte stöds av den aktuella modulen. |
En lista över fel som är specifika för Studio-moduler (klassiska) finns i Machine Learning Felkoder.
En lista över API-undantag finns i Machine Learning REST API-felkoder.