Поделиться через

Применение преобразований в Direct2D

  • Статья

В рисовании с помощью Direct2Dмы увидели, что метод ID2D1RenderTarget::FillEllipse рисует эллипс, ориентированный по осям x и y. Но предположим, что вы хотите нарисовать эллипс, наклоненный под углом?

изображение, показывающее наклонный эллипс.

С помощью преобразований можно изменить фигуру следующими способами.

  • Поворот вокруг точки.
  • Масштабирование.
  • Перемещение (смещение в направлении X или Y).
  • Скос (также известный как сдвиг).

Преобразование — это математическая операция, которая сопоставляет набор точек с новым набором точек. Например, на следующей схеме показан треугольник, повернутый вокруг точки P3. После применения поворота точка P1 сопоставляется с P1', точка P2 сопоставляется с P2', а точка P3 сопоставляется с самой собой.

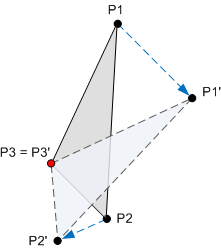
схему, показывющую поворот вокруг точки.

Преобразования реализуются с помощью матриц. Тем не менее, вам не нужно понимать математику матриц, чтобы использовать их. Если вы хотите узнать больше о математике, см. в приложении : Преобразования матрицы.

Чтобы применить преобразование в Direct2D, вызовите метод ID2D1RenderTarget::SetTransform. Этот метод принимает D2D1_MATRIX_3X2_F структуру, которая определяет преобразование. Эту структуру можно инициализировать, вызвав методы в классе D2D1::Matrix3x2F. Этот класс содержит статические методы, возвращающие матрицу для каждого типа преобразования:

Например, следующий код применяет поворот на 20 градусов вокруг точки (100, 100).

pRenderTarget->SetTransform(
    D2D1::Matrix3x2F::Rotation(20, D2D1::Point2F(100,100)));

Преобразование применяется ко всем последующим операциям рисования, пока не вызовете SetTransform. Чтобы удалить текущее преобразование, вызовите SetTransform с матрицей удостоверений. Чтобы создать матрицу удостоверений, вызовите функцию Matrix3x2F::Identity.

pRenderTarget->SetTransform(D2D1::Matrix3x2F::Identity());

Рисование стрелок часов

Давайте воспользуемся преобразованиями, преобразовав нашу программу круг в аналоговые часы. Это можно сделать, добавив линии для рук.

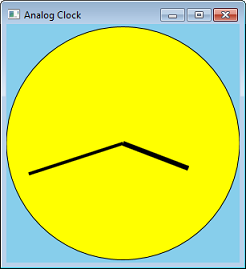
снимок экрана аналоговой программы часов.

Вместо вычисления координат для линий можно вычислить угол, а затем применить преобразование поворота. В следующем коде показана функция, которая рисует одну часовую руку. Параметр fAngle дает угол руки в градусах.

void Scene::DrawClockHand(float fHandLength, float fAngle, float fStrokeWidth)
{
    m_pRenderTarget->SetTransform(
        D2D1::Matrix3x2F::Rotation(fAngle, m_ellipse.point)
            );

    // endPoint defines one end of the hand.
    D2D_POINT_2F endPoint = D2D1::Point2F(
        m_ellipse.point.x,
        m_ellipse.point.y - (m_ellipse.radiusY * fHandLength)
        );

    // Draw a line from the center of the ellipse to endPoint.
    m_pRenderTarget->DrawLine(
        m_ellipse.point, endPoint, m_pStroke, fStrokeWidth);
}

Этот код рисует вертикальную линию, начиная с центра циферблата и заканчивая точкой конечной точки. Линия поворачивается вокруг центра эллипса с помощью преобразования вращения. Центральная точка поворота — это центр эллипса, который формирует циферблат часов.

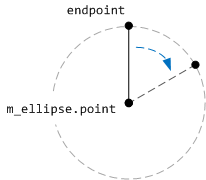
схему, показывающую вращение часовой стрелки.

В следующем коде показано, как рисуется весь циферблат часов.

void Scene::RenderScene()
{
    m_pRenderTarget->Clear(D2D1::ColorF(D2D1::ColorF::SkyBlue));

    m_pRenderTarget->FillEllipse(m_ellipse, m_pFill);
    m_pRenderTarget->DrawEllipse(m_ellipse, m_pStroke);

    // Draw hands
    SYSTEMTIME time;
    GetLocalTime(&time);

    // 60 minutes = 30 degrees, 1 minute = 0.5 degree
    const float fHourAngle = (360.0f / 12) * (time.wHour) + (time.wMinute * 0.5f);
    const float fMinuteAngle =(360.0f / 60) * (time.wMinute);

    DrawClockHand(0.6f,  fHourAngle,   6);
    DrawClockHand(0.85f, fMinuteAngle, 4);

    // Restore the identity transformation.
    m_pRenderTarget->SetTransform( D2D1::Matrix3x2F::Identity() );
}

Вы можете скачать полный проект Visual Studio из примера Пример часов Direct2D. (Просто для удовольствия, загружаемая версия добавляет радиальный градиент к циферблату часов.)

Объединение преобразований

Четыре основных преобразования можно объединить путем умножения двух или более матриц. Например, следующий код объединяет поворот с переводом.

const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(20);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(40, 10);

pRenderTarget->SetTransform(rot * trans);

Класс Matrix3x2F предоставляетоператора*() для умножения матрицы. Порядок умножения матриц важен. Установка преобразования (M × N) означает "Применить M первым, а затем N". Например, ниже приводится вращение, за которым следует перевод:

схему, на которой показан поворот, за которым следует перевод.

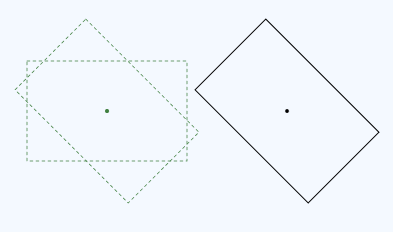
Ниже приведен код для этого преобразования:

const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(rot * trans);

Теперь сравните это преобразование с преобразованием в обратном порядке: сначала перемещение, затем вращение.

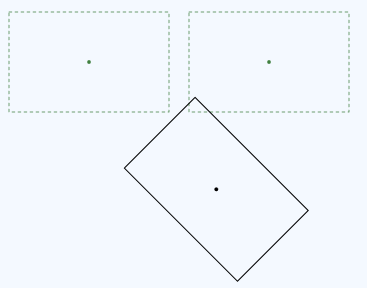
схему, на которой показан перевод, за которым следует поворот.

Поворот выполняется вокруг центра исходного прямоугольника. Ниже приведен код для этого преобразования.

D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(trans * rot);

Как видно, матрицы одинаковы, но порядок операций изменился. Это происходит потому, что умножение матрицы не является коммутативным: M × N ≠ N × M.

Далее

Приложение . Матрицные преобразования