Поделиться через

Предварительно вычисляемая передача radiance (Direct3D 9)

  • Статья

Использование предварительно вычисляемой передачи сияния

В интересных сценах присутствует несколько форм сложности, в том числе моделирование среды освещения (то есть модели освещения площади и точечно-направленного), а также смоделирование глобальных эффектов (например, тени, межрефлексии, подповерхностное рассеяние). Традиционные методы интерактивной отрисовки моделировают ограниченную сложность. PRT обеспечивает эти эффекты с некоторыми значительными ограничениями:

  • Объекты считаются жесткими (т. е. без деформаций).
  • Это объектно-ориентированный подход (если объекты не перемещаются вместе, эти глобальные эффекты не поддерживаются между ними).
  • Смоделировано только низкочастотное освещение (в результате чего возникают мягкие тени). Для высокочастотных огней (резкие тени) придется использовать традиционные методы.

PRT требует одно из следующих, но не оба:

  • Модели с высоким уровнем тесселяции и vs_1_1
  • ps_2_0

Стандартное диффузное освещение и PRT

Следующий рисунок отображается с использованием традиционной (n · l) модели освещения. Резкие тени можно включить с помощью другого прохода и некоторой формы техники затенения (карты глубины тени или объемы теней). Добавление нескольких огней потребует либо нескольких проходов (если требуется использовать тени), либо более сложных шейдеров с традиционными методами.

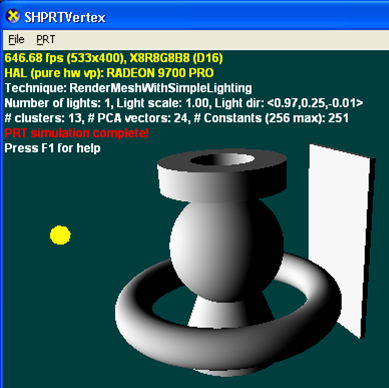
снимок экрана: иллюстрация, отображаемая с использованием традиционной модели освещения

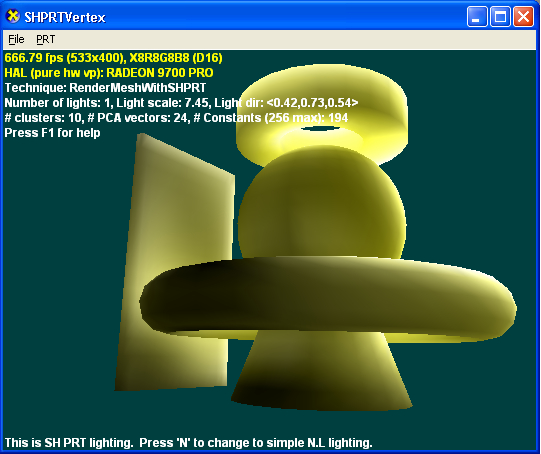
Следующая иллюстрация отрисовывается с помощью PRT с использованием наилучшего приближения к одному направленному свету, который он может разрешить. Это приводит к мягким тени, которые было бы трудно производить с помощью традиционных методов. Так как PRT всегда моделирует полные среды освещения, добавляя несколько огней или используя карту среды, вы будете изменять только значения (но не количество) констант, используемых шейдером.

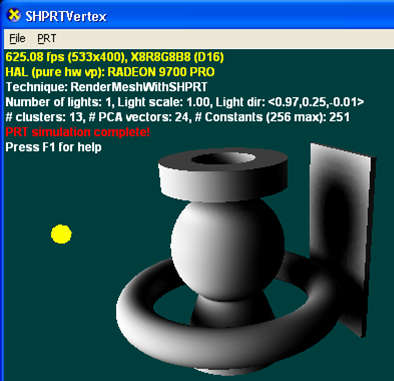
Снимок экрана: иллюстрация, отображаемая с помощью prt

PRT с интерфлексиями

Прямое освещение достигает поверхности непосредственно от света. Межрефлексии — это свет, достигающий поверхности после отскакивания от какой-то другой поверхности несколько раз. PRT может моделировать это поведение, не изменяя производительность во время выполнения, просто запустив симулятор с разными параметрами.

На следующем рисунке используется только прямой PRT (0 отказов без межрефлексий).

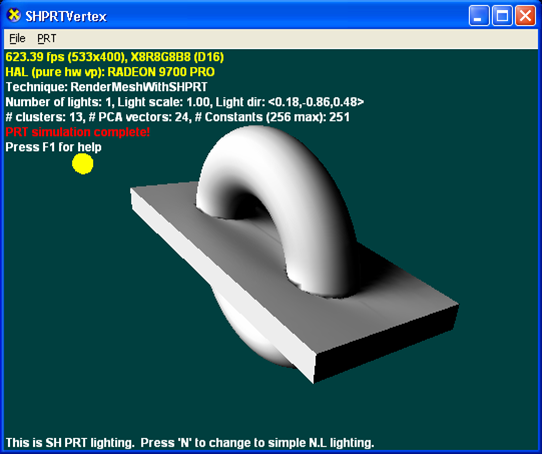
Снимок экрана: иллюстрация, отображаемая только с использованием прямого prt

Следующий рисунок создан с использованием PRT с интерфлексиями (2 отскакивания с интерфлексиями).

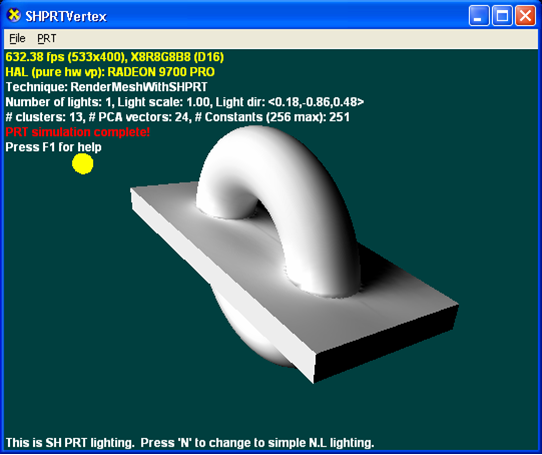
Снимок экрана: иллюстрация, отображаемая с помощью prt с интерфлексиями

PRT с подповерхностным рассеяние

Подповерхностное рассеяние — это метод, который моделирует прохождение света через определенные материалы. Например, нажмите на ладони освещенный фонарик. Свет от фонарика проходит через вашу руку, отскакивает вокруг (меняя цвет в процессе), и выходит с другой стороны руки. Это также можно смоделировать с помощью простых изменений в симуляторе и без изменений в среде выполнения.

На следующем рисунке показано PRT с подповерхностным рассеяние.

снимок экрана: иллюстрация, отображаемая с помощью prt с подповерхностным рассеяние

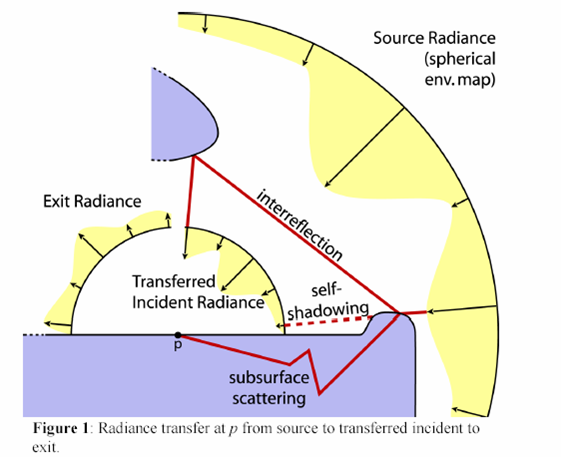
Принцип работы PRT

Следующие термины полезны для понимания принципов работы PRT, как показано на следующей схеме.

Исходное сияние. Исходное сияние представляет среду освещения в целом. В PRT произвольное окружение аппроксимируется с помощью сферической гармонической основы - это освещение считается удаленным относительно объекта (то же предположение, что и с картами среды).

Выходное сияние: выходное сияние — это свет, исходящий из точки на поверхности из любого возможного источника (отраженное сияние, подповерхностное рассеяние, излучение).

Векторы передачи. Векторы передачи сопоставляют сияние источника с исходящим сиянием и предварительно вычисляются в автономном режиме с помощью сложной имитации переноса света.

Схема работы prt

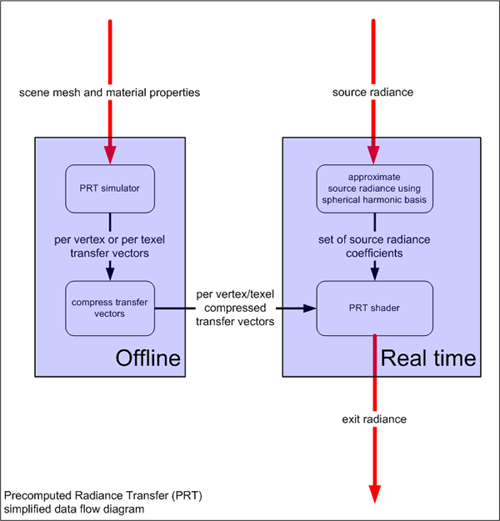
PRT разделяет процесс отрисовки на два этапа, как показано на следующей схеме:

  1. Дорогостоящее моделирование переноса легких данных предварительно вычисляет коэффициенты передачи, которые можно использовать во время выполнения.
  2. Относительно легкий этап времени выполнения сначала приблизит среду освещения с использованием сферической гармонической основы, а затем использует эти коэффициенты освещения и предварительно вычисляемые коэффициенты передачи (с этапа 1) с простым шейдером, что приводит к выходу сияния (свет покидает объект).

Схема потока данных prt

Использование API PRT

  1. Вычисление векторов передачи с помощью одного из вычислений... методы ID3DXPRTEngine.

    Для непосредственной работы с этими векторами передачи требуется значительный объем памяти и вычислений шейдера. Сжатие значительно сокращает объем памяти и необходимых вычислений шейдера.

    Окончательные значения освещения вычисляются в вершинном шейдере, который реализует следующее сжатое уравнение отрисовки.

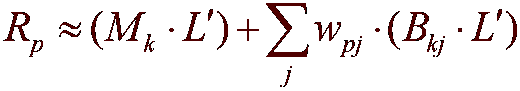
    уравнение отрисовки prt

    Где:

    Параметр Описание
    Rp Один канал выходного сияния в вершине p и вычисляется на каждой вершине сетки.
    Mk Среднее значение для кластера k. Это вектор коэффициентов Order².
    k Идентификатор кластера для вершины p.
    L' Приближение исходного сияния к базовым функциям SH. Это вектор коэффициентов Order².
    j Целое число, которое суммирует по количеству векторов PCA.
    wpj Jth PCA вес для точки p. Это один коэффициент.
    Bkj Базовый вектор Jth PCA для кластера k. Это вектор коэффициентов Order².

     

    Извлечение... методы ID3DXPRTCompBuffer предоставляют доступ к сжатым данным из имитации.

  2. Вычисление исходного сияния.

    В API есть несколько вспомогательных функций для обработки различных распространенных сценариев освещения.

    Функция Назначение
    D3DXSHEvalDirectionalLight Приближение к обычному направленному свету.
    D3DXSHEvalSphericalLight Приблизительные локальные сферические источники света. (Обратите внимание, что PRT работает только с удаленными средами освещения.)
    D3DXSHEvalConeLight Приблизительный источник света в удаленной области. Примером может быть солнце (очень маленький угол конуса).
    D3DXSHEvalHemisphereLight Оценивает свет, представляющий собой линейную интерполяцию между двумя цветами (по одному на каждом полюсе сферы).

     

  3. Вычисление сияния выхода.

    Теперь уравнение 1 необходимо вычислять в каждой точке с помощью вершины или пиксельного шейдера. Перед оценкой шейдера необходимо предварительно вычислить константы и загрузить их в таблицу констант (дополнительные сведения см. в демонстрационном примере PRT ). Сам шейдер является простой реализацией этого уравнения.

    struct VS_OUTPUT
{
    float4 Position   : POSITION;   // vertex position 
    float2 TextureUV  : TEXCOORD0;  // vertex texture coordinates 
    float4 Diffuse    : COLOR0;     // vertex diffuse color
};

VS_OUTPUT Output;   
Output.Position = mul(vPos, mWorldViewProjection);

float4 vExitR = float4(0,0,0,0);
float4 vExitG = float4(0,0,0,0);
float4 vExitB = float4(0,0,0,0);

for (int i=0; i < (NUM_PCA_VECTORS/4); i++) 
{
   vExitR += vPCAWeights[i] * 
       vClusteredPCA[iClusterOffset+i+1+(NUM_PCA_VECTORS/4)*0];
   vExitG += vPCAWeights[i] * 
       vClusteredPCA[iClusterOffset+i+1+(NUM_PCA_VECTORS/4)*1];
   vExitB += vPCAWeights[i] * 
       vClusteredPCA[iClusterOffset+i+1+(NUM_PCA_VECTORS/4)*2];
}

float4 vExitRadiance = vClusteredPCA[iClusterOffset];
vExitRadiance.r += dot(vExitR,1);
vExitRadiance.g += dot(vExitG,1);
vExitRadiance.b += dot(vExitB,1);

Output.Diffuse = vExitRadiance;

Ссылки

Дополнительные сведения о PRT и сферической гармонике см. в следующих статьях:

Precomputed Radiance Transfer for Real-Time Rendering in Dynamic, 
Low-Frequency Lighting Environments 
P.-P. Sloan, J. Kautz, J. Snyder
SIGGRAPH 2002 

Clustered Principal Components for Precomputed Radiance Transfer 
P.-P. Sloan, J. Hall, J. Hart, J. Snyder 
SIGGRAPH 2003 

Efficient Evaluation of Irradiance Environment Maps 
P.-P. Sloan 
ShaderX 2,  W. Engel 

Spherical Harmonic Lighting: The Gritty Details 
R. Green 
GDC 2003 

An Efficient Representation for Irradiance Environment Maps 
R. Ramamoorthi, P. Hanrahan 

A Practical Model for Subsurface Light Transport 
H. W. Jensen, S. R. Marschner, M. Levoy, and P. Hanrahan 
SIGGRAPH 2001 

Bi-Scale Radiance Transfer 
P.-P. Sloan, X. Liu, H.-Y. Shum, J. Snyder
SIGGRAPH 2003 

Fast, Arbitrary BRDF Shading for Low-Frequency Lighting Using Spherical 
Harmonics 
J. Kautz, P.-P. Sloan, J. Snyder
12th Eurographics Workshop on Rendering 

Precomputing Interactive Dynamic Deformable Scenes 
D. James, K. Fatahalian 
SIGGRAPH 2003 

All-Frequency Shadows Using Non-linear Wavelet Lighting Approximation 
R. Ng, R. Ramamoorth, P. Hanrahan 
SIGGRAPH 2003 

Matrix Radiance Transfer 
J. Lehtinen, J. Kautz
SIGGRAPH 2003 

Math World 
E. W. Weisstein, Wolfram Research, Inc. 

Quantum Theory of Angular Momentum 
D. A. Varshalovich, A.N. Moskalev, V.K. Khersonskii

Дополнительные разделы

Уравнения PRT (Direct3D 9)

Представление PRT с текстурами (Direct3D 9)

ID3DXPRTBuffer

ID3DXPRTCompBuffer

ID3DXPRTEngine

ID3DXTextureGutterHelper

Предварительно вычисляемые функции передачи сияния

Математические функции