Кубит в квантовых вычислениях
Как и бит, который является основным объектом информации в классических вычислениях, кубит (квантовый бит) является основным объектом информации в квантовых вычислениях. Для разъяснения этой аналогии в этой статье рассматривается простейший пример: одиночный кубит.
Представление кубита
В то время как бит (или двоичная цифра) может иметь значение $0$ или $1$, кубит может иметь значение $0$, $1$ или квантовую суперпозицию $0$ и $1$.
Состояние одиночного кубита можно описать с помощью двумерного вектора-столбца единичной нормы, то есть сумма квадратов его записей должна равняться $ 1 $. Этот вектор, называемый вектором квантового состояния, содержит всю информацию, необходимую для описания однокубитной квантовой системы, точно так же, как один бит содержит всю информацию, необходимую для описания состояния двоичной переменной. Основы векторов и матриц в квантовых вычислениях см. в разделе "Вектор" и "Матрицы".
Любой двумерный вектор-столбец с реальными или комплексными числами и нормой $1$ представляет возможное квантовое состояние кубита. Таким образом, $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ представляет состояние кубита, если $\alpha$ и $\beta$ являются комплексными числами, удовлетворяющими условию $|\alpha|^2 + |\beta|^2 = 1$. Некоторые примеры допустимых векторов квантовых состояний, представляющих кубиты, включают
$$\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \end{bmatrix}, \begin{bmatrix}\frac{{1}{\sqrt{2}}\\\frac{{1}{\sqrt{2}}\end{bmatrix}, \begin{bmatrix}\frac{1}{\sqrt{{2}}\\\frac{{-1}{\sqrt{2}}\end{bmatrix}, \text{ и }\begin{bmatrix}\frac{1}{\sqrt{{2}}\\\frac{i}{\sqrt{2}}\end{bmatrix}.$$
Векторы квантовых состояний $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ и $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ приобретают особое значение. Эти два вектора образуют базу для векторного пространства, описывающего состояние кубита. Это означает, что любой вектор квантового состояния может быть записан как сумма этих базовых векторов. В частности, вектор $\begin{bmatrix} x \\ y \end{bmatrix}$ может быть записан как $x \begin{bmatrix} 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Хотя любой поворот этих векторов будет служить вполне допустимой базой для кубита, выбран именно этот и назван вычислительной базой.
Эти два квантовых состояния выбраны для соответствия двум состояниям классического бита, а именно $0$ и $1$. Обычно выбирают
$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \qquad 1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix},$$
хотя противоположный выбор также допустим. Таким образом, из-за неограниченного количества возможных векторов однокубитных квантовых состояний только два из них соответствуют состояниям классических битов, чего нельзя сказать об остальных квантовых состояниях.
Измерение кубита
При объяснении того, как можно представить кубит, можно получить некоторое представление о том, что представляют собой эти состояния, обсудив концепцию измерения. Измерение является реализацией идеи "изучения" кубита, позволяющей моментально свернуть квантовое состояние в одно или два классических состояния $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ или $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. При измерении кубита, заданного с помощью вектора квантового состояния $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ получаем значение $0$ с вероятностью $|\alpha|^2$ и значение $1$ с вероятностью $|\beta|^2$. При значении $0$ новым состоянием кубита является $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$; при значении $1$ его состоянием является $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Обратите внимание, что сумма этих вероятностей равна $1$ из-за условия нормализации $|\alpha|^2 + |\beta|^2 = 1$.
Свойства измерения также означают, что общий знак вектора квантового состояния не имеет значения. Инвертирование вектора эквивалентно $\alpha\rightстрелке -\alpha$ и $\beta\rightстрелке -\beta$. Так как вероятность измерения $0$ и $1$ зависит от квадрата терминов, вставка таких знаков совершенно не влияет на вероятности. Такие этапы обычно называются "глобальными", и в более общих случаях они могут иметь вид $e^{i \phi}$, а не просто $\pm 1$.
Последнее важное свойство измерения заключается в том, что оно не обязательно приводит к повреждению всех векторов квантовых состояний. Если в начале у нас есть кубит в состоянии $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$, что соответствует классическому состоянию $0$, в результате измерения этого состояния мы всегда будем получать $0$ и квантовое состояние останется без изменений. В этом смысле, если присутствуют только классические биты (например, кубиты со значениями $\begin{bmatrix}1 \\ 0 \end{bmatrix}$ или $\begin{bmatrix}0 \\ 1 \end{bmatrix}$), то измерение не приводит к повреждению системы. Это означает, что можно реплицировать классические данные и управлять ими на квантовом компьютере точно так же, как на классическом компьютере. Однако возможность хранить информацию в обоих состояниях одновременно создает преимущество квантовых вычислений перед возможностями классических вычислений, а также снижает вероятность того, что квантовые компьютеры будут копировать квантовые данные без разбора, см. также раздел Теорема о запрете клонирования.
Визуализация кубитов и преобразований с помощью области Blockh
Кубиты можно также представить в $3$D, используя сферу Блоха. Сфера Блоха является одним из методов описание однокубитного квантового состояния (которое является двухмерным комплексным вектором) в виде трехмерного вещественнозначного вектора. Это важно, поскольку метод позволяет визуализировать однокубитные состояния и, таким образом, продолжать рассуждения, что может оказать неоценимую помощь в понимании многокубитных состояний (для которых, к сожалению, сфера Блоха не подходит). Сферу Блоха можно представить следующим образом:
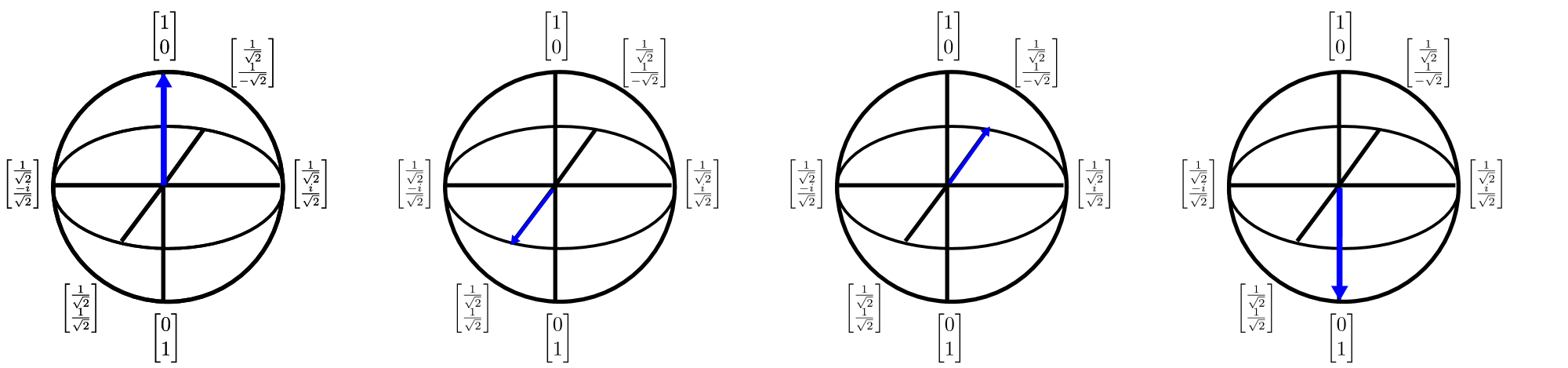
Стрелки на этой схеме показывают направление, в котором указывает вектор квантового состояния, и каждое изменение стрелки можно представить как поворот относительно одной из основных осей. Рассмотрение квантовых вычислений как последовательности поворотов является многообещающей догадкой, однако эту догадку сложно применить в разработке и описании алгоритмов. Q# упрощает эту проблему за счет создания языка для описания таких поворотов.
Однокубитные операции
Квантовые компьютеры обрабатывают данные путем применения универсального набора квантовых ворот, которые могут эмулировать любой поворот вектора квантового состояния. Это понятие универсальности является аналогом универсальности для традиционных (например, классических) вычислений, когда набор ворот считается универсальным, если каждое преобразование входных битов может быть выполнено с использованием цепи ограниченной длины. В квантовых вычислениях допустимые преобразования, которые можно выполнять с кубитами, являются унитарными преобразованиями и измерениями. Смежная операция или комплексно сопряженное транспонирование имеет критически важное значение для квантовых вычислений, так как оно необходимо для инвертирования квантовых преобразований.
Операции с одним кубитом или однокубитные квантовые ворота можно классифицировать по двум категориям: ворота Clifford и ворота, отличные от Клиффорда. Не Клиффорд ворота состоят только из $$T-ворота (также известный $как \pi/8$ ворота).
$$T=\begin{bmatrix} 1 amp; 0 0 &\\ amp; e^{i\pi/4\end{bmatrix}}.& $$
Стандартный набор однокубитных ворот Clifford, включенный по умолчанию в Q#, include
$$H=\frac{{2}}\begin{bmatrix}{1}{\sqrt{ 1 & \\ 1 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 0 \\ amp; i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 && 1 \\&ам; 0 \end{bmatrix}= HT^4H,$$
$$Y =\begin{bmatrix} 0 amp; -i \\ & 0 &\end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1& 0\\ 0&-1 \end{bmatrix}=T^4. $$
Здесь операции $X$, $Y$ и $Z$ используются особенно часто и называются операторами Паули по имени их создателя Вольфганга Паули. Эти операции можно использовать вместе с неклиффордскими воротами ($T$-ворота) для аппроксимации любого унитарного преобразования с одним кубитом.
Показанные выше ворота относятся к числу наиболее популярных простейших ворот для описания операций на логическом уровне стека (представьте логический уровень в качестве уровня квантового алгоритма), однако часто бывает удобнее рассмотреть менее простые операции на уровне алгоритма, например операции ближе к уровню описания функции. К счастью, Q# также содержит методы, доступные для реализации унитарных объектов более высокого уровня, которые, в свою очередь, позволяют реализовать высокоуровневые алгоритмы без явного разложения всех элементов до ворот Клиффорда и $ T $ -ворот.
Простейшей из таких базовых операций является однокубитный поворот. Обычно рассматриваются три однокубитных поворота: $R_x$, $R_y$ и $R_z$. Например, чтобы визуализировать действие поворота $R_x(\theta)$, представьте, что большой палец правой руки указывает в направлении оси $x$ в сфере Блоха, а поворот вектора – это поворот руки на угол $\theta/2$ радианов. Этот сложный для понимания коэффициент $2$ возникает из того факта, что если отрисовать ортогональные векторы в сфере Блоха, они будут удалены друг от друга на $180^\circ$, хотя на самом деле геометрически они удалены друг от друга на $90^\circ$. Соответствующие унитарные матрицы:
\begin{выравнивание*}& R_z(\theta) = e^{-i\theta Z/2}=\begin{bmatrix} e^{-i\theta/2&}amp; 0 0\\& amp; e^{i\theta/2\end{bmatrix}}, \\& R_x(\theta) e^{-i\theta X/2=} HR_z(\theta)H =\begin{bmatrix} \cos(\theta/2) amp; -i\sin(\theta/2)\\ -i\sin(\theta/2&) & \cos(\theta/2) \end{bmatrix}, \\& = R_y(\theta) e^{-i\theta Y/2=} SHR_z(\theta)HS^ \cos(=\begin{bmatrix}\dagger\theta/2) amp; -\sin(\theta/2)\\ \sin(\theta/2) && \cos(\theta/2) \end{bmatrix}. = \end{align*}
Любые три поворота можно объединить для выполнения произвольного поворота в трех измерениях, и это можно увидеть в сфере Блоха: любую унитарную матрицу можно также записать в виде последовательности трех поворотов. В частности, для каждой унитарной матрицы $U$ существует $\alpha,\beta,\gamma,\delta$ такое, что $U= e^{i\alpha} R_x(\beta)R_z(\gamma)R_x(\delta)$. Таким образом, $R_z(\theta)$ и $H$ также образуют универсальный набор ворот, хотя этот набор не является дискретным, поскольку $\theta$ может принимать любое значение. По этой причине и из-за приложений в квантовом моделировании такие непрерывные ворота крайне важны для квантовых вычислений, особенно на уровне разработки квантового алгоритма. Чтобы получить отказоустойчивую аппаратную реализацию, в конечном итоге, они будут скомпилированы в дискретные последовательности ворот, которые приблизятся к этим поворотам.