Обозначения на схемах квантовых цепей

Иногда квантовые алгоритмы проще понять на схеме каналов, чем в эквивалентном письменном представлении матрицы. В этой статье объясняется, как читать схемы квантовых каналов и их соглашения.

Дополнительные сведения см. в статье "Визуализация схем квантовых каналов".

Чтение схем квантовых каналов

В квантовой цепи время течет слева направо. Квантовые ворота упорядочиваются в хронологическом порядке, при этом первыми к кубитам применяются крайние ворота слева.

Рассмотрим следующую схему квантовых каналов в качестве примера:

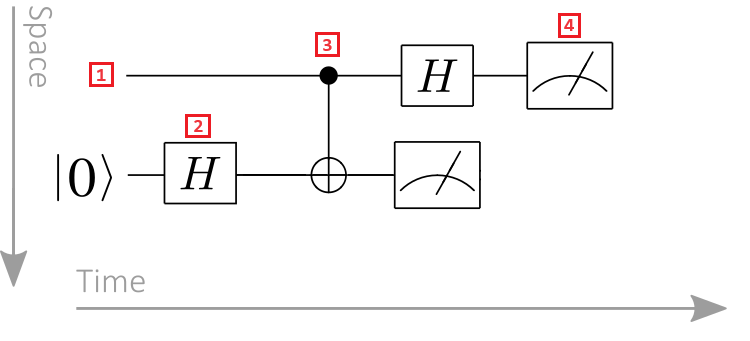
1. Регистр Кубита: регистры Кубита отображаются как горизонтальные линии, с каждой строкой, представляющей кубитов. Верхняя строка — кубитовая регистрация с меткой 0, вторая строка — это кубитовая регистрация с меткой 1 и т. д.
2. Квантовые ворота: квантовые операции представлены квантовыми воротами. Термин квантовый вентиль является аналогом классических логических вентилей. Ворота, действующие на один или несколько регистров кубита, обозначаются в виде прямоугольника. В этом примере символ представляет операцию Hadamard.
3. Контролируемые ворота: контролируемые ворота действуют на два или более кубитов. В этом примере символ представляет ворота CNOT. Черный круг представляет кубит элемента управления, а крест внутри круга представляет target кубит.
4. Операция измерения: символ измерения представляет операцию измерения. Операция измерения принимает регистр кубита в качестве входных и выходных данных классической информации.

Применение квантовых шлюзов

Так как время проходит слева направо, левый большинство ворот применяется сначала, например, действие следующего квантового канала является унитарной матрицей $CBA$.

Примечание.

Матричное умножение подчиняется противоположному правилу: сначала применяется крайняя матрица справа. Однако в схемах квантовых цепей сначала применяется крайние ворота слева. Это различие иногда может приводить к путанице, поэтому важно обратить внимание на это существенное различие между линейной алгебраической нотацией и схемами квантовых цепей.

Входы и выходы квантовых цепей

На схеме квантовых каналов провода, вводимые квантовыми воротами, представляют кубиты, входные в квантовые ворота, и провода, выходя из квантовых ворот, представляют кубиты, которые выводятся из квантовых ворот.

Число входных данных квантового шлюза равно количеству выходных данных квантовых ворот. Это связано с тем, что квантовые операции являются унитарными и, следовательно, обратимыми. Если квантовые ворота имеют больше выходных данных, чем входные данные, это не будет обратимо и, следовательно, не унитарным, что является противоречием.

По этой причине любой прямоугольник, нарисованный на схеме цепи, должен иметь одинаковое число проводов на входе и на выходе.

Операции с несколькими кубитами

Схемы многокубитных цепей составляются аналогично схемам однокубитных цепей. Например, двухкубитная унитарная операция $B$ может быть определена $как (H S\otimes X),$ поэтому эквивалентный квантовый канал имеет следующий тип:

Можно также рассмотреть $B$ как действие с одним двухкубитным регистром, а не с двумя однокубитными регистрами, в зависимости от контекста использования цепи.

Возможно, наиболее полезным свойством таких обобщенных схем цепей является то, что они позволяют описывать сложные квантовые алгоритмы на высоком уровне без необходимости их компиляции в фундаментальные ворота. Это означает, что можно разработать идеи о потоках данных в больших квантовых алгоритмах без необходимости изучения всех сведений о том, как работает каждая из подпрограмм в алгоритме.

Контролируемые ворота

Квантовые контролируемые ворота — это два кубита, которые применяют один кубитовый шлюз к target кубите, если контрольный кубит находится в определенном состоянии.

Например, рассмотрим квантовые управляемые ворота, обозначаемые $\Lambda(G),$ где значение одного кубита управляет применением $операции G$ . Управляемые ворота $\Lambda(G)$ можно понять, взглянув на следующий пример входных данных состояния продукта:

$\Lambda(G) (\alpha\ket{{0} + \beta\ket{1}) \ket{\psi}=\alpha\ket{{0}\ket{\psi} + \beta\ket{{1} G\ket{\psi}$

Другими словами, управляемые ворота применяют $G$ к регистру, содержащему $\psi$, если и только если управляющий кубит принимает значение $1$. Как правило, такие управляемые операции описаны на схемах каналов следующим символом:

Черным кружком обозначен квантовый бит, из которого идет управление воротами, а вертикальный провод обозначает унитарность, которая применяется, когда управляющий кубит принимает значение $1$.

В особых случаях, когда $G=X$ и $G=Z$, для описания управляемой версии ворот используется следующая нотация (обратите внимание, что контролируемые ворота X — это ворота CNOT):

Q# позволяет применять методы автоматического создания управляемой версии операции, которая освобождает программиста от необходимости писать код этих операций вручную. Такой пример приведен далее:

operation PrepareSuperposition(qubit : Qubit) : Unit
is Ctl { // Auto-generate the controlled specialization of the operation
    H(qubit);
}

Классически контролируемые ворота

Квантовые ворота также можно применять после измерения, где результат измерения действует как классический бит управления.

Следующий символ представляет классически контролируемый шлюз, где $G$ применяется к биту классического элемента управления значение $1$:

Оператор измерения

Операции измерения принимают регистр кубита, измеряет его и выводит результат в виде классической информации.

Операция измерения обозначается символом счетчика и всегда принимает в качестве входных данных регистр кубита (обозначается сплошной линией) и выводит классическую информацию (обозначается двойной линией). В частности, символ операции измерения выглядит следующим образом:

Measure В Q#операторе реализуется операция измерения.

Пример: унитарное преобразование

Рассмотрим унитарное преобразование $\text{ CNOT}_{01}(H\otimes 1)$. Эта последовательность ворот имеет основополагающее значение для квантовых вычислений, так как она создает максимально запутанное двухкубитное состояние:

$\mathrm{CNOT}_{01}(H\otimes 1)\ket{00}=\frac{1}{\sqrt{2}}\left(\ket{{00} + \ket{11}\right),$

Операции такой или более высокой сложности повсеместны в квантовых алгоритмах и исправлении квантовых ошибок.

Схема цепи для подготовки этого максимально запутанного квантового состояния:

Символ за воротами Hadamard представляет ворота CNOT, где черный круг указывает контрольный кубит и крест в круге указывает target кубит. Для работы этой квантовой цепи используются два кубита (или два регистра, состоящие из одного кубита).

Пример: схема канала телепортации

Квантовое телепортирование является одним из лучших квантовых алгоритмов для иллюстрации компонентов канала.

Квантовое телепортирование — это протокол, позволяющий передавать квантовое состояние из одного кубита в другой с помощью общего спутанного состояния между отправителем и получателем и классическим обменом данными между ними.

В целях обучения отправитель называется Алиса, получатель называется Бобом, а кубит, который должен быть телепортирован, называется кубитом сообщения. Алиса и Боб держат один кубит каждый, и Алиса имеет дополнительный кубит, который является кубитом сообщения.

На следующей схеме канала показан протокол телепортации:

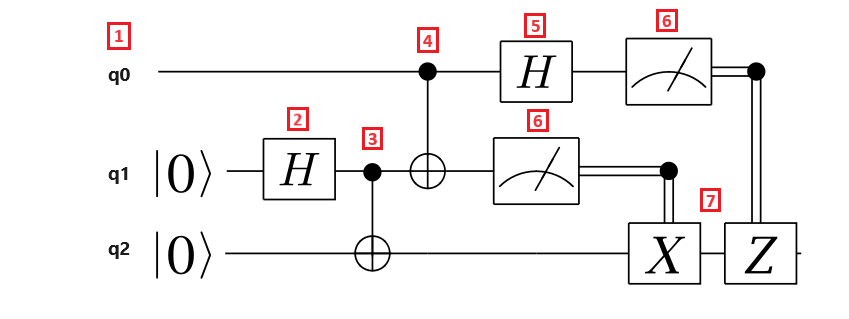
Давайте разберем шаги протокола телепортации:

1. Кубит регистр q0 является кубитом сообщения, кубит регистр q1 является кубитом Алисы, а кубит регистр q2 является кубитом Боба. Кубит сообщения находится в неизвестном состоянии, и Алиса и кубиты Боба находятся в $\ket{0}$ состоянии.
2. Ворота Hadamard применяются к кубитам Алисы. Так как кубит находится в $\ket{0}$ состоянии, итоговое состояние — $\frac{1}{\sqrt{{2}}(\ket{{0} + \ket{1})$.
3. Ворота CNOT применяются к Алисе и кубитам Боба. Кубит Алисы является контрольным кубитом, и кубит Боба является target кубитом. Итоговое состояние — $\frac{{1}{\sqrt{2}}(\ket{00} + \ket{{11})$. Алиса и Боб теперь разделяют запутанное состояние.
4. Шлюз CNOT применяется к кубитам сообщения и кубитом Алисы. Так как кубит Алисы также запутан с кубитом Боба, результирующее состояние является трехкубитным запутанным состоянием.
5. К кубитам сообщения применяется шлюз Hadamard.
6. Алиса измеряет ее два кубита и сообщает результаты измерения Бобу, который не отражается в цепи. Результаты измерения являются двумя классическими битами, которые могут принимать значения 00, 01, 10 или 11.
7. Два классически контролируемых шлюза Паули X и Z применяются к кубитам Боба в зависимости от значения $результата 1$. Итоговое состояние — исходное состояние кубита сообщения.

Связанный контент

• Квантовое запутание
• Алгоритм Гровера
• Квантовое промежуточное представление
• Векторы и матрицы