Avaliar a função de probabilidade
Importante
O suporte para o Estúdio de ML (clássico) terminará a 31 de agosto de 2024. Recomendamos a transição para o Azure Machine Learning até essa data.
A partir de 1 de dezembro de 2021, não poderá criar novos recursos do Estúdio de ML (clássico). Até 31 de agosto de 2024, pode continuar a utilizar os recursos existentes do Estúdio de ML (clássico).
- Consulte informações sobre projetos de machine learning em movimento de ML Studio (clássico) para Azure Machine Learning.
- Saiba mais sobre Azure Machine Learning.
A documentação do Estúdio de ML (clássico) está a ser descontinuada e poderá não ser atualizada no futuro.
Ajusta uma função de distribuição de probabilidade especificada a um conjunto de dados
Categoria: Funções Estatísticas
Nota
Aplica-se a: Machine Learning Studio (clássico) apenas
Módulos semelhantes de arrasto e queda estão disponíveis em Azure Machine Learning designer.
Visão geral do módulo
Este artigo descreve como usar o módulo de Função de Probabilidade avaliar em Machine Learning Studio (clássico), para calcular medidas estatísticas que descrevem a distribuição de uma coluna, como as distribuições de Bernoulli, Pareto ou Poisson.
Para utilizar este modelo, ligue um conjunto de dados que contenha pelo menos uma coluna de valores numéricos e escolha uma distribuição de probabilidade para testar. O módulo devolve uma tabela de dados que contém valores da função de probabilidade especificada.
Pode calcular qualquer um destes valores para a distribuição de probabilidades escolhida:
- função de distribuição cumulativa (cdf)
- função de distribuição cumulativa inversa (InverseCdf)
- função de densidade de probabilidade (Pdf)
Por que a distribuição de probabilidades é útil?
Quando avalia os seus dados com uma distribuição de probabilidades, está a mapear valores de colunas contra um conjunto de valores com propriedades conhecidas. Ao saber se os seus dados correspondem a uma destas distribuições bem conhecidas, poderá inferir outras propriedades dos seus dados. Em geral, pode obter melhores previsões a partir de um modelo quando pode identificar a distribuição que melhor se adequa aos dados.
A questão de qual função de distribuição de probabilidades depende dos dados e das variáveis que estão a ser medidas. Por exemplo, algumas distribuições são concebidas para descrever probabilidades de valores discretos; outros destinam-se a ser utilizados apenas com variáveis numéricas contínuas. Para algumas distribuições, também deve saber antecipadamente uma média esperada, graus de liberdade, etc. Para mais detalhes, consulte distribuições de probabilidades suportadas
Como configurar avaliar a função de probabilidade
Todas as opções mudam dependendo do tipo de distribuição de probabilidade que pretende calcular. Se alterar o método de distribuição de probabilidades, outras seleções que possa ter feito são reiniciadas.
Portanto, não se esqueça de escolher primeiro a opção Distribuição !
O conjunto de dados utilizado como entrada deve conter dados numéricos. Outros tipos de dados são ignorados.
Para cada análise, pode aplicar um único método de distribuição de probabilidade. Para calcular uma distribuição de probabilidade diferente, adicione uma instância separada do módulo para cada distribuição que pretende testar.
Adicione o módulo de função de probabilidade de avaliação à sua experiência. Pode encontrar este módulo na categoria Funções Estatísticas no Machine Learning Studio (clássico).
Ligação um conjunto de dados que contém pelo menos uma coluna de números.
Utilize a opção Distribuição para selecionar o tipo de distribuição de probabilidades que pretende calcular. Consulte as distribuições de probabilidades suportadas para obter uma lista de opções e os seus argumentos necessários.
Desa estada quaisquer parâmetros que sejam necessários pela distribuição.
Escolha uma das três estatísticas a criar: a função de distribuição cumulativa (cdf), a função de distribuição cumulativa inversa (InverseCdf)ou a função de densidade de probabilidade (pdf).
Consulte a secção de notas técnicas para definições.
Utilize o seletor de colunas para escolher as colunas sobre as quais calcular a distribuição de probabilidades selecionada.
Todas as colunas selecionadas devem ter um tipo de dado numérico.
O leque de dados na coluna também deve ser válido, dada a função de probabilidade selecionada. Caso contrário, poderá ocorrer um erro ou resultado naN.
Para colunas escassas, quaisquer valores que correspondam a zeros de fundo não serão processados.
Utilize a opção modo Resultado para especificar como obter os resultados. Pode substituir os valores da coluna pelos valores de distribuição de probabilidade, anexar os novos valores ao conjunto de dados ou devolver apenas os valores de distribuição de probabilidade.
Executar a experiência ou clicar com o botão direito no módulo de Função de Probabilidade de Avaliação e clique em Executar selecionado.
Resultados
A tabela a seguir contém um exemplo de resultados, utilizando a opção Apêndice , numa única coluna de temperatura do conjunto de dados da amostra de Incêndios Florestais .
| temp | StandardNormal.Cdf (temporário) | StandardNormal.Pdf(temporário) | FFisher.cdf (temporário | FFisher.cdf (temporário |
|---|---|---|---|---|
| 8.2 | 1 | 1 | 0.984774 | 0.004349 |
| 18 | 1 | 1 | 0.997896 | 0.000311 |
| 14.6 | 1 | 1 | 0.996352 | 0.000648 |
| 8.3 | 1 | 1 | 0.985201 | 0.004187 |
| 11,4 | 1 | 1 | 0.993147 | 0.001502 |
As rubricas das colunas geradas contêm a distribuição de probabilidades que foi utilizada.
Se não tiver a certeza de qual a distribuição de probabilidade suscetível de se adequar aos seus dados, pode criar um gráfico rápido de distribuição cumulativa e densidade de probabilidade para qualquer coluna numérica.
- Clique com o botão direito na saída do conjunto de dados ou no módulo e selecione Visualize.
- Selecione a coluna de interesse, e no painel Histogram, selecione distribuição cumulativa ou densidade de probabilidade.
- Um gráfico da distribuição, como o seguinte, é sobreposto no histograma que representa os dados.
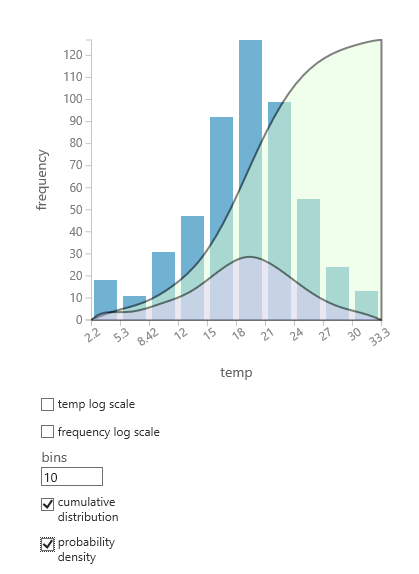
Distribuição de probabilidades suportadas
O módulo de Função de Probabilidade avaliar suporta as seguintes distribuições:
Rio Bernoulli
A distribuição de Bernoulli é uma distribuição sobre valores binários: por outras palavras, modela a distribuição esperada quando apenas dois valores são possíveis.
Para calcular, selecione Bernoulli e deseminete as seguintes opções:
- Probabilidade de sucesso
O parâmetro p especifica a probabilidade de um 1 ser gerado. Digite um número (float) entre 0.0 e 1.0 que especifica a probabilidade de sucesso. O padrão é .5.
Beta
A distribuição Beta é uma distribuição contínua de univariados.
Para calcular, selecione Beta e desa estale as seguintes opções:
Forma
Digite um valor para alterar a forma da distribuição.Um parâmetro de forma é qualquer parâmetro de uma distribuição de probabilidade que não define a sua localização ou escala. Portanto, quando introduz um valor para a forma, o parâmetro muda a forma da distribuição em vez de se mover, esticar ou encolher.
O valor deve ser um número (
double). O padrão é 1.0.Dimensionamento
Digite um número para utilizar para escalonar a distribuição.Aplicando um valor de escala à distribuição, pode encolher ou esticá-lo.
O valor predefinido é 1.0. Os valores devem ser números positivos.
Limite superior
Digite um número (double) que represente o limite superior da distribuição. O padrão é 1.0.Limite inferior
Digite um número (double) que represente o limite inferior da distribuição. O padrão é 0.0.
Binomial
A distribuição binomial é uma distribuição discreta e univariada. A distribuição binomial é usada para modelo o número de sucessos numa amostra. A substituição é utilizada durante a amostragem. Para amostragem sem substituição, utilize a distribuição Hypergeometric.
Para calcular, selecione Binomial e deseguite as seguintes opções:
Probabilidade de sucesso
Digite um número (float) entre 0.0 e 1.0 que indique a probabilidade de sucesso. O padrão é .5.Número de ensaios
Especifique o número de julgamentos.Utilize um
integer, com um valor mínimo de 1. O padrão é 3.
Cauchy
A distribuição cauchy é uma distribuição de probabilidade contínua simétrica.
Para calcular, selecione Cauchy e desa estale as seguintes opções:
Localização
Digite um número (double) que represente a localização do 0th elemento.Ao especificar um valor para o parâmetro Localização , pode deslocar a distribuição de probabilidade para cima ou para baixo numa escala numérica.
O padrão é 0.0.
Estação Chisquare
A distribuição chi-quadrada é uma soma dos quadrados de variáveis k independentes, padrão, normais e aleatórias.
Para calcular, selecione ChiSquare e deseguihe as seguintes opções:
- Número de graus de liberdade Digite um número (
double) para especificar os graus de liberdade. O padrão é 1.0.
ChiSquareRightTailed
Esta opção proporciona uma distribuição chi-quadrada de cauda direita.
Para calcular, selecione ChiSquareRight Tailed e desere as seguintes opções:
- Número de graus de liberdade
Digite um número (double) para especificar os graus de liberdade. O padrão é 1.0.
Exponencial
A distribuição exponencial é uma distribuição sobre os números reais parametrizados por um parâmetro não negativo.
Para calcular, selecione Exponencial e deseguite as seguintes opções:
- Rio Lambda
Digite um número (double) para usar como parâmetro lambda. O padrão é 1.0.
FFisher
Gera a probabilidade da estatística fisher para uma amostra, também conhecida como a distribuição F de Fisher. Esta distribuição é de duas caudas.
Para calcular, selecione FFisher e deseguite as seguintes opções:
Numeradores graus de liberdade
Digite um número (double) para especificar os graus de liberdade que são usados no numerador. O padrão é 3.0.Denominadores de liberdade
Digite um número (double) para especificar os graus de liberdade que são usados no denominador. O padrão é 6.0.
FFisherRightTailed
Cria uma distribuição de Fisher de cauda direita. A distribuição fisher também é conhecida como a distribuição de Fisher F, distribuição de Snedecor, ou distribuição Fisher-Snedecor. Esta forma particular de distribuição é de cauda direita.
Para calcular, selecione FFisherRight Tailed e desere as seguintes opções:
Numeradores graus de liberdade
Digite um número (double) para especificar os graus de liberdade que são usados no numerador. O padrão é 3.0.Denominadores de liberdade
Digite um número (double) para especificar os graus de liberdade que são usados no denominador. O padrão é 6.0.
Gama
A distribuição gama é uma família de distribuição contínua de probabilidades com dois parâmetros. Por exemplo, chi-quadrado é um caso especial da distribuição gama.
Para calcular, selecione Gama e desa estale as seguintes opções:
Dimensionamento
Digite um valor a utilizar para escalonar a distribuição.Aplicando um valor de escala à distribuição, pode encolher ou esticá-lo.
O valor predefinido é 1.0. Os valores devem ser números positivos.
Localização
Digite um número (double) que represente a localização do 0th elemento.Ao especificar um valor para o parâmetro Localização , pode deslocar a distribuição de probabilidade para cima ou para baixo numa escala numérica.
O padrão é 0.0.
GeneralizadosExtremeValues
Cria uma distribuição desenvolvida para lidar com valores extremos. A distribuição generalizada de valor extremo (GEV) é na verdade um grupo de distribuições contínuas de probabilidades que combina as distribuições gumbel, Fréchet e Weibull (também conhecidas como distribuição de valor extremo tipo I, II e III).
Para obter mais informações sobre a teoria do valor extremo, consulte este artigo na Wikipédia: teorema de Fisher-Tippet-Gnedenko.
Para calcular, selecione GeneralizedExtremeValues e desaprote as seguintes opções:
Forma
Digite um valor para alterar a forma da distribuição.Um parâmetro de forma é qualquer parâmetro de uma distribuição de probabilidade que não define a sua localização ou escala. Portanto, quando introduz um valor para a forma, o parâmetro muda a forma da distribuição em vez de se mover, esticar ou encolher.
O valor deve ser um número (
double). O padrão é 1.0.Dimensionamento
Digite um valor a utilizar para escalonar a distribuição.Aplicando um valor de escala à distribuição, pode encolher ou esticá-lo.
O valor predefinido é 1.0. Os valores devem ser números positivos.
Localização
Digite um número (double) que represente a localização do 0th elemento.Ao digitar um valor para o parâmetro Localização , pode deslocar a distribuição de probabilidade para cima ou para baixo numa escala numérica.
O padrão é 0.0.
Geométrico
A distribuição geométrica é uma distribuição sobre números inteiros positivos parametrizados por um número real positivo.
Para calcular, selecione Geométrico e deseguite as seguintes opções:
- Probabilidade de sucesso
Digite um número (float) entre 0.0 e 1.0 que indique a probabilidade de sucesso. O padrão é .5.
Nota
Esta implementação da distribuição geométrica não gera zeros.
GumbelMax
A distribuição gumbel é uma das várias distribuições de valor extremo. A opção GumbelMax implementa a distribuição máxima de valor extremo tipo 1.
Para calcular, selecione GumbelMax e desere nas seguintes opções:
Dimensionamento
Digite um valor a utilizar para escalonar a distribuição.Aplicando um valor de escala à distribuição, pode encolher ou esticá-lo.
O valor predefinido é 1.0. Os valores devem ser números positivos.
Localização
Digite um número (double) que represente a localização do 0th elemento.Ao digitar um valor para o parâmetro Localização , pode deslocar a distribuição de probabilidade para cima ou para baixo numa escala numérica.
O padrão é 0.0.
GumbelMin
A distribuição gumbel é uma das várias distribuições de valor extremo. A distribuição gumbel também é referida como a distribuição de menor valor extremo (SEV) ou a distribuição de menor valor extremo (Tipo I). A opção GumbelMin implementa a distribuição mínima de valor extremo tipo 1.
Para calcular, selecione GumbelMin e deve definir as seguintes opções:
Dimensionamento
Digite um valor a utilizar para escalonar a distribuição.Aplicando um valor de escala à distribuição, pode encolher ou esticá-lo.
O valor predefinido é 1.0. Os valores devem ser números positivos.
Localização
Digite um número (double) que represente a localização do 0th elemento.Ao digitar um valor para o parâmetro Localização , pode deslocar a distribuição de probabilidade para cima ou para baixo numa escala numérica.
O padrão é 0.0.
Hipergeométrico
A distribuição hipergeométrica é uma distribuição discreta de probabilidade que descreve o número de sucessos numa sequência de n draws de uma população finita sem substituição, assim como a distribuição binomial descreve o número de sucessos para sorteios com substituição.
Para calcular, selecione Hypergeometric e desenôs as seguintes opções:
Número de amostras
Digite um inteiro que indique o número de amostras a utilizar. O padrão é 9.Número de sucesso
Digite um inteiro que defina o valor para o sucesso. O padrão é 24.Tamanho da população
Especifique o tamanho da população a utilizar ao estimar a distribuição hipergeométrica.
Rio Laplace
A distribuição de Laplace é uma distribuição sobre os números reais, parametrizada por um parâmetro de escala e por um parâmetro de escala.
Para calcular, selecione a distribuição de Laplace e desem teça as seguintes opções:
Dimensionamento
Digite um valor a utilizar para escalonar a distribuição.Aplicando um valor de escala à distribuição, pode encolher ou esticá-lo.
O valor predefinido é 1.0. Os valores devem ser números positivos.
Localização
Digite um número (double) que represente a localização do 0th elemento.Ao digitar um valor para o parâmetro Localização , pode deslocar a distribuição de probabilidade para cima ou para baixo numa escala numérica.
O padrão é 0.0.
Logística
A distribuição logística é semelhante à distribuição normal, mas não tem limite no lado esquerdo da distribuição. A distribuição logística é utilizada em modelos de regressão logística e rede neural e para modelar dados de ciências da vida.
Para calcular, selecione Logística e desa estalem as seguintes opções:
Dimensionamento
Digite um valor a utilizar para escalonar a distribuição.Aplicando um valor de escala à distribuição, pode encolher ou esticá-lo.
O valor predefinido é 1.0. Os valores devem ser números positivos.
Média
Digite um número (double)que indique o valor médio estimado da distribuição. O padrão é 0.0.
Lognormal
A distribuição lognormal é uma distribuição contínua de univariados.
Para calcular, selecione Lognormal e deseguite as seguintes opções:
Média
Digite um número (double) que indique o valor médio estimado da distribuição. O padrão é 0.0.Desvio padrão
Digite um número positivo (double) que indique o desvio padrão estimado da distribuição. O padrão é 1.0.
NegativoBino
A distribuição binomial negativa é uma distribuição sobre os números naturais com dois parâmetros (r, p). No caso especial que r é um inteiro, pode interpretar a distribuição como o número de caudas antes da cabeça derth quando a probabilidade da cabeça é p.
Para calcular, selecione NegativeBinomial e desaprote as seguintes opções:
Probabilidade de sucesso
Digite um número (float) entre 0.0 e 1.0 que indique a probabilidade de sucesso. O padrão é .5.Número de sucesso
Digite um inteiro que especifique o valor para o sucesso. O padrão é 24.
Normal
A distribuição normal também é conhecida como a distribuição gaussiana.
Para calcular, selecione Normal e desa estale as seguintes opções:
Média
Digite um número (double) que indique o valor médio estimado da distribuição. O padrão é 0.0.Desvio padrão
Digite um número positivo (double) que indique o desvio padrão estimado da distribuição. O padrão é 1.0.
Rio Pareto
A distribuição de Pareto é uma distribuição de probabilidades de lei de poder que coincide com a distribuição social, científica, geofísica, atuarial, e muitos outros tipos de fenómenos observáveis.
Para calcular, selecione Pareto e desa estale as seguintes opções:
Forma
Digite um valor (opcional) para alterar a forma da distribuição.Um parâmetro de forma é qualquer parâmetro de uma distribuição de probabilidade que não define a sua localização ou escala. Portanto, quando introduz um valor para a forma, o parâmetro muda a forma da distribuição em vez de se mover, esticar ou encolher.
O valor deve ser um número (
double). O padrão é 1.0.Dimensionamento
Digite um valor (opcional) para alterar a escala da distribuição. Aplicando um valor de escala à distribuição, pode encolher ou esticá-lo.O valor deve ser um número (
double). O padrão é 1.0.
Poisson
Nesta implementação, o método de Knuth é usado para gerar variáveis aleatórias distribuídas por Poisson. Para obter mais informações sobre a distribuição de Poisson, consulte Poisson Regression.
Para calcular, selecione Poisson e desa estale as seguintes opções:
- Média
Digite um número (double) que indique o valor médio estimado da distribuição. O padrão é 0.0.
Rio Rayleigh
A distribuição de Rayleigh é uma distribuição contínua de probabilidades. Como exemplo de como surge, a velocidade do vento terá uma distribuição rayleigh se os componentes do vetor de velocidade do vento bidimensional não estiverem correlacionados e normalmente distribuídos com igual variação.
Para calcular, selecione Rayleigh e desa estale as seguintes opções:
- Limite inferior
Digite um número (double) que represente o limite inferior da distribuição. O padrão é 0.0.
StandardNormal
Esta opção proporciona a distribuição normal padrão, sem outros parâmetros.
Para calcular, selecione StandardNormal e selecione as colunas.
TStudent
Esta opção implementa a distribuição t do estudante univariado.
Para calcular, selecione TStudent e desacorra as seguintes opções:
- Número de graus de liberdade
Digite um número (double) para especificar os graus de liberdade. O padrão é 1.0.
TStudentRightTailed
Implementa a distribuição t do estudante univariado usando uma cauda direita.
Para calcular, selecione TStudentRightTailed e deseguihe as seguintes opções:
- Número de graus de liberdade
Digite um número (double) para especificar os graus de liberdade. O padrão é 1.0.
TStudentTwoTailed
Implementa a distribuição de t-distribuição de um estudante de duas caudas.
Para calcular, selecione TStudentTwoTailed e desacorra as seguintes opções:
- Número de graus de liberdade
Digite um número (double) para especificar os graus de liberdade. O padrão é 1.0.
Uniforme
A distribuição uniforme também é conhecida como a distribuição retangular.
Para calcular, selecione Uniforme e desa esta medida as seguintes opções:
Limite inferior
Digite um número (double) que represente o limite inferior da distribuição. O padrão é 0.0.Limite superior
Digite um número (double) que represente o limite superior da distribuição. O padrão é 1.0.
Weibull
A distribuição weibull é amplamente utilizada na engenharia de fiabilidade. Pode utilizar o seu parâmetro De Forma para modelo muitas outras distribuições.
Para calcular, selecione Weibull e deseguite as seguintes opções:
Forma
Digite um valor (opcional) para alterar a forma da distribuição.Um parâmetro de forma é qualquer parâmetro de uma distribuição de probabilidade que não define a sua localização ou escala. Portanto, quando introduz um valor para a forma, o parâmetro muda a forma da distribuição em vez de se mover, esticar ou encolher.
O valor deve ser um número (
double). O padrão é 1.0.Dimensionamento
Digite um valor (opcional) para alterar a escala da distribuição. Aplicando um valor de escala à distribuição, pode encolher ou esticá-lo.O valor deve ser um número (
double). O padrão é 1.0.
Notas técnicas
Esta secção contém detalhes de implementação, dicas e respostas a perguntas frequentes.
Detalhes de implementação
Este módulo suporta todas as distribuições fornecidas na biblioteca open source MATH.NET Numéricas. Para mais informações, consulte a documentação para a biblioteca Math.Net.Numerics.Distribution .
As distribuições de cauda direita e de duas caudas aparecem como distribuições separadas, e não como versões parametrizadas das distribuições de bases. O comportamento atual é preservar a compatibilidade com Excel.
Definições
Este módulo suporta o cálculo de qualquer um destes valores para a distribuição especificada:
cdf, ou a função de distribuição cumulativa
Devolve a probabilidade de um evento composto, definido como a soma das ocorrências quando a variável aleatória toma um valor menor do que algum valor específico x.
Por outras palavras, responde à pergunta: "Quão comuns são as amostras que são inferiores ou iguais a este valor?"
Esta função pode ser utilizada com variáveis numéricas contínuas e discretas.
InverseCdf, ou a função de distribuição cumulativa inversa
Devolve o valor associado a um valor de probabilidade cumulativo específico (cdf).
Por outras palavras, responde à pergunta: "Qual é o valor de x em que a função cdf devolve a probabilidade cumulativa y?"
pdf, ou a função de densidade de probabilidade
Descreve a probabilidade relativa de uma variável aleatória ser um valor específico.
Por outras palavras, responde à pergunta: "Quão comuns são as amostras exatamente a este valor?"
Entradas esperadas
| Nome | Tipo | Description |
|---|---|---|
| Conjunto de dados | Tabela de Dados | Conjunto de dados de entrada |
Parâmetros do módulo
| Nome | Intervalo | Tipo | Predefinição | Description |
|---|---|---|---|---|
| Distribuição | Qualquer | ProbabilidadeDistribução | StandardNormal | Selecione o tipo de distribuição de probabilidade para gerar. |
| Método | Qualquer | ProbabilidadeDistributionMethod | CDF | Selecione o método a utilizar no cálculo da distribuição de probabilidades selecionada. As opções são a função de distribuição cumulativa (cdf), a função de distribuição cumulativa inversa (InverseCdf) e a função de densidade de probabilidade ou função de massa (pdf). |
| Método de distribuição binomial negativo | Qualquer | ProbabilidadeDistributionMethodForNegativeBinomial | CDF | Se selecionar a distribuição binomial negativa, especifique o método utilizado para avaliar a distribuição. |
| Probabilidade de sucesso | [0.0;1.0] | Float | 0,5 | Digite um valor para usar como probabilidade de sucesso. |
| Forma | Qualquer | Float | 1.0 | Digite um valor que modifie a forma da distribuição. |
| Escala | >=0.0 | Float | 1.0 | Digite um valor que altera a escala da distribuição para expandi-la ou encolher em tamanho. |
| Número de ensaios | >=1 | Número inteiro | 3 | Especifique o número de julgamentos. |
| Limite inferior | Qualquer | Float | 0,0 | Digite um número para usar como o limite inferior da distribuição |
| Limite superior | Qualquer | Float | 1.0 | Digite um número para usar como limite superior da distribuição |
| Localização | Qualquer | Float | 0,0 | Digite a localização do elemento zero na distribuição. |
| Número de graus de liberdade | Qualquer | Float | 1.0 | Especifique o número de graus de liberdade. |
| Numeradores graus de liberdade | Qualquer | Float | 3.0 | Especificar o número de graus de liberdade no numerador. |
| Denominadores de liberdade | Qualquer | Float | 6,0 | Especificar o número de graus de liberdade no denominador. |
| Rio Lambda | >=0.0 | Float | 1.0 | Especifique um valor para o parâmetro Lambda. |
| Número de amostras | Qualquer | Número inteiro | 9 | Especifique o número de amostras. |
| Número de sucesso | Qualquer | Número inteiro | 24 | Digite um valor para usar como número de sucesso. |
| Tamanho da população | Qualquer | Número inteiro | 52 | Especificar o tamanho da população. |
| Média | Qualquer | Float | 0,0 | Digite o valor médio estimado. |
| Desvio padrão | >=0.0 | Float | 1.0 | Digite o desvio padrão estimado. |
| Conjunto de colunas | Qualquer | Seleção de Colunas | Escolha as colunas sobre as quais calcular a distribuição de probabilidades. | |
| Modo resultado | Qualquer | OutputTo | ResultadoSOnly | Especificar como os resultados serão guardados no conjunto de dados de saída. As opções são anexar novas colunas, substituir colunas existentes ou apenas obter os resultados. |
Saída
| Nome | Tipo | Description |
|---|---|---|
| Conjunto de dados de resultados | Tabela de Dados | Conjunto de dados de saída |
Exceção
Para obter uma lista completa de mensagens de erro, consulte códigos de erro do módulo.
| Exceção | Description |
|---|---|
| Erro 0017 | A exceção ocorre se uma ou mais colunas especificadas tiverem um tipo que não é suportado pelo módulo atual. |
Para obter uma lista de erros específicos dos módulos Studio (clássicos), consulte Machine Learning Códigos de Erro.
Para obter uma lista de exceções da API, consulte Machine Learning CÓDIGOs de Erro da API REST.