Correlação Linear compute
Importante
O suporte para o Estúdio de ML (clássico) terminará a 31 de agosto de 2024. Recomendamos a transição para o Azure Machine Learning até essa data.
A partir de 1 de dezembro de 2021, não poderá criar novos recursos do Estúdio de ML (clássico). Até 31 de agosto de 2024, pode continuar a utilizar os recursos existentes do Estúdio de ML (clássico).
- Consulte informações sobre projetos de machine learning em movimento de ML Studio (clássico) para Azure Machine Learning.
- Saiba mais sobre Azure Machine Learning.
A documentação do Estúdio de ML (clássico) está a ser descontinuada e poderá não ser atualizada no futuro.
Calcula a correlação linear entre os valores da coluna num conjunto de dados
Categoria: Funções Estatísticas
Nota
Aplica-se a: Machine Learning Studio (clássico) apenas
Módulos semelhantes de arrasto e queda estão disponíveis em Azure Machine Learning designer.
Visão geral do módulo
Este artigo descreve como usar o módulo de correlação linear compute no Machine Learning Studio (clássico), para calcular um conjunto de coeficientes de correlação Pearson para cada par possível de variáveis no conjunto de dados de entrada.
O coeficiente de correlação pearson, às vezes chamado teste R de Pearson, é um valor estatístico que mede a relação linear entre duas variáveis. Ao examinar os valores do coeficiente, pode inferir algo sobre a força da relação entre as duas variáveis, e se estão positivamente correlacionados ou negativamente correlacionados.
Como configurar a correlação linear
Antes de calcular o coeficiente de correlação, existem alguns pré-requisitos, tais como a limpeza dos seus dados e a verificação de que a relação entre as variáveis é adequada para este módulo. Também deve remover ou imputar valores em falta.
Aplicam-se as seguintes restrições ao utilizar este módulo:
O módulo de correlação linear compute pode processar apenas valores numéricos. Todos os outros tipos de valores, incluindo valores em falta, valores não numéricos e valores categóricos, são tratados como NaNs.
A correlação de Pearson é calculada para todas as colunas numéricas no conjunto de dados que são passadas como entrada. Certifique-se de excluir quaisquer colunas adequadas para esta análise.
A Correlação Linear computacional não pode ser utilizada com dados que têm valores em falta.
Passo 1: Determinar a linearidade
Se não se espera que as colunas que está a testar tenham algum tipo de relação linear, não faz sentido gerar este coeficiente. Portanto, é uma boa ideia testar as colunas primeiro, para ver se têm o tipo certo de dados e o tipo certo de distribuição em geral.
Existem várias formas de determinar se a relação entre as colunas é aproximadamente linear:
Crie um enredo disperso das variáveis em Studio (clássico), utilizando a opção Visualize no conjunto de dados. Clique numa das colunas variáveis numéricas, expanda visualizações e clique em comparar. Selecione uma variável diferente, e um enredo de dispersão é gerado automaticamente. Se um tipo diferente de enredo for gerado, significa que pelo menos uma coluna tem um tipo de dados diferente (não numérico).
Calcular uma equação de regressão para as duas variáveis. Existem muitos pacotes R que suportam isto, que você pode carregar e usar no módulo Executar R Script .
Passo 2: Limpar dados
Deve remover ou preencher valores em falta, remover ou cortar os outliers e certificar-se de que as colunas têm o tipo de dados adequado.
Certifique-se de verificar se existem espaços reservados e substitua este valor por outros valores apropriados antes de utilizar este módulo. Se as NaNs forem inseridas para valores em falta quando o conjunto de dados foi carregado a partir da fonte, pode causar um erro. Valores de espaço reservado, tais como 999 ou -1 também podem causar maus resultados.
Para preparar os seus dados, pode utilizar estes módulos:
Pode ajustar o tipo de dados das colunas utilizando Metadados de Edição. Certifique-se de que as colunas que pretende analisar estão marcadas como colunas de características.
Passo 3: Gerar o coeficiente
Adicione o módulo de correlação linear compute à sua experiência. Pode encontrar este módulo na categoria Funções Estatísticas no Machine Learning Studio (clássico).
Adicione o conjunto de dados que pretende analisar.
Recomendamos que adicione um módulo Select Columns in Dataset entre o conjunto de dados e o módulo de correlação linear compute , para remover colunas desnecessárias. Configure as Colunas Selecionadas no módulo Dataset para obter apenas as duas colunas numéricas para as quais pretende calcular coeficientes.
Caso contrário, o módulo de correlação linear compute pode gerar muitas colunas de NaNs.
Não há parâmetros para definir para este módulo. No entanto, falhará se as colunas que passa como entradas não satisfaçam os requisitos.
Execute a experimentação.
Resultados para duas colunas
Tendo em conta duas colunas de características, o módulo de correlação linear compute devolve o coeficiente de correlação do momento de correlação scalar Pearson (amostra). O coeficiente de correlação Pearson (muitas vezes denotado como r) varia em valor de +1 a -1.
+1indica uma forte relação linear positiva-1indica uma forte correlação linear negativa0não denota nenhuma relação linear entre as duas variáveis.
A interpretação dos coeficientes depende muito do problema que está a modelar e das variáveis que está a estudar. Assim, é importante compreender o contexto dos dados ao relatar e interpretar o coeficiente de correlação de Pearson.
Se tem a certeza de que as variáveis não estão relacionadas e, no entanto, o coeficiente de correlação da Pearson é fortemente positivo (r.5 > ou mais), deve investigar mais.
Se utilizar a correlação linear em duas variáveis que sabe estar perfeitamente correlacionada, e os valores do coeficiente não forem o que se espera, pode indicar um problema nos dados.
Resultados para mais de duas colunas
Dada uma matriz (isto é, mais de duas colunas de recurso), o módulo de correlação linear compute devolve um conjunto de correlações de momento do produto Pearson entre cada par de colunas de recurso.
Portanto, o resultado é uma tabela n x n contendo os coeficientes para cada combinação das colunas n . Se alguma coluna não cumprir os critérios, é devolvida uma NaN ("não um número") de volta.
Por exemplo, assuma que passou nas duas colunas numéricas wheel-base e curb-weight mais uma coluna categórica ( make do conjunto de dados de preços do Automóvel). O resultado é uma tabela 3x3 de coeficientes para todas as combinações possíveis das colunas de entrada:
make |
wheel-base |
curb-weight |
|---|---|---|
| Rio Nan | Rio Nan | Rio Nan |
| Rio Nan | 1 | 0.776386 |
| Rio Nan | 0.776386 | 1 |
Nesta tabela, entende-se que as filas representam cada uma das variáveismakewheel-base, e curb-weightpor essa ordem.
- O valor r para a correlação de
wheel-basesi mesmo é 1. - O valor r para a correlação de
wheel-basea quecurb-weighté de 0,776386. - Todas as correlações que envolvem a coluna
makeresultam em NaN, incluindo a correlação com si mesma, porquemakeé uma característica de corda.
Recomendamos que remova colunas não numéricas, para evitar tabelas complexas com muitos valores sem sentido.
Exemplos
Para ver como este módulo é usado em experiências de machine learning, consulte a Galeria Azure AI:
- Processamento e Análise de Dados: Esta amostra demonstra múltiplas técnicas para modificar os seus dados. A Correlação Linear compute é usada para identificar colunas de funcionalidades potenciais.
Notas técnicas
Esta secção contém detalhes de implementação, dicas e respostas a perguntas frequentes.
Detalhes de implementação
Se a coluna que é passada como entrada contiver escalares, as matrizes de entrada (x e y) são tratadas como vetores e a correlação de momento do produto Pearson é calculada da seguinte forma:
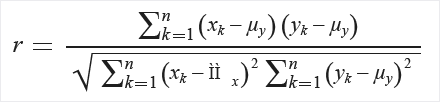
Nesta fórmula, cada matriz contém n elementos e os meios das amostras x e y são μx e μy respectivamente.
Para uma matriz, uma matriz de dados (X) é a entrada, na qual cada coluna representa um vetor de valores. A matriz de dados deve ser n-by-m. A saída é a matriz m-by-m, R como definido por
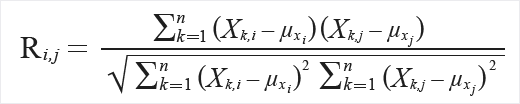
Nesta fórmula, o μx representa o valor médio da coluna xi. Os elementos em I,j sempre iguais 1, pois representam a correlação de um vetor com si mesmo.
Entradas esperadas
| Nome | Tipo | Description |
|---|---|---|
| Conjunto de dados | Tabela de Dados | Conjunto de dados de entrada |
Saídas
| Nome | Tipo | Description |
|---|---|---|
| Conjunto de dados de resultados | Tabela de Dados | Matriz de correlações |
Exceções
| Exceção | Description |
|---|---|
| Erro 0003 | A exceção ocorre se uma ou mais entradas forem nulas ou vazias. |
| Erro 0020 | A exceção ocorre se o número de colunas em alguns dos conjuntos de dados passados para o módulo for demasiado pequeno. |
| Erro 0021 | A exceção ocorre se o número de linhas em alguns dos conjuntos de dados passados para o módulo for demasiado pequeno. |
Para obter uma lista de erros específicos dos módulos Studio (clássicos), consulte Machine Learning Códigos de Erro.
Para obter uma lista de exceções da API, consulte Machine Learning CÓDIGOs de Erro da API REST.