Uso de uma matriz de cores para transformar uma única cor

O Windows GDI+ fornece as classes Image e Bitmap para armazenar e manipular imagens. Os objetos Image e Bitmap armazenam a cor de cada pixel como um número de 32 bits: 8 bits cada para vermelho, verde, azul e alfa. Cada um dos quatro componentes é um número de 0 a 255, sendo que 0 representa nenhuma intensidade e 255 representa intensidade total. O componente alfa especifica a transparência da cor: 0 é completamente transparente e 255 é totalmente opaca.

Um vetor de cor é uma tupla de 4 do formulário (vermelho, verde, azul, alfa). Por exemplo, o vetor de cor (0, 255, 0, 255) representa uma cor opaca que não tem nenhum vermelho nem azul, mas tem verde na intensidade total.

Outra convenção para representar cores usa o número 1 para intensidade máxima e o número 0 para intensidade mínima. Usando essa convenção, a cor descrita no parágrafo anterior seria representada pelo vetor (0, 1, 0, 1). O GDI+ usa a convenção de 1 como intensidade total quando executa transformações de cor.

Você pode aplicar transformações lineares (rotação, dimensionamento e similares) a vetores de cor multiplicando por uma matriz de 4 ×4. No entanto, você não pode usar uma matriz de 4 ×4 para executar uma tradução (não linear). Se você adicionar uma quinta coordenada fictícia (por exemplo, o número 1) a cada um dos vetores de cor, poderá usar uma matriz de 5 ×5 para aplicar qualquer combinação de transformações lineares e traduções. Uma transformação que consiste em uma transformação linear seguida por uma translação é chamada de transformação afim. Uma matriz de 5 ×5 que representa uma transformação affine é chamada de matriz homogênea para uma transformação de 4 espaços. O elemento na quinta linha e quinta coluna de uma matriz homogênea de 5 ×5 deve ser 1 e todas as outras entradas na quinta coluna devem ser 0.

Por exemplo, suponha que você queira começar com a cor (0,2, 0,0, 0,4, 1,0) e aplicar as seguintes transformações:

1. Duplicar o componente vermelho
2. Adicionar 0,2 aos componentes vermelhos, verdes e azuis

A multiplicação de matriz a seguir executará o par de transformações na ordem listada.

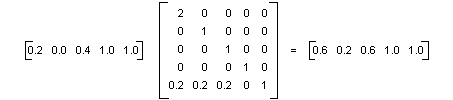
Os elementos de uma matriz de cores são indexados (baseados em zero) por linha e coluna. Por exemplo, a entrada na quinta linha e na terceira coluna da matriz M é indicada por M[4][2].

A matriz de identidade 5 ×5 (mostrada na ilustração a seguir) tem 1s na diagonal e 0s em qualquer outro lugar. Se você multiplicar um vetor de cor pela matriz de identidade, o vetor de cor não mudará. Uma maneira conveniente de formar a matriz de uma transformação de cor é começar com a matriz de identidade e fazer uma pequena alteração que produza a transformação desejada.

Para uma discussão mais detalhada de matrizes e transformações, consulte Sistemas de coordenadas e transformações.

O exemplo a seguir usa uma imagem toda de uma cor (0,2, 0,0, 0,4, 1,0) e aplica a transformação descrita nos parágrafos anteriores.

Image            image(L"InputColor.bmp");
ImageAttributes  imageAttributes;
UINT             width = image.GetWidth();
UINT             height = image.GetHeight();

ColorMatrix colorMatrix = {
   2.0f, 0.0f, 0.0f, 0.0f, 0.0f,
   0.0f, 1.0f, 0.0f, 0.0f, 0.0f,
   0.0f, 0.0f, 1.0f, 0.0f, 0.0f,
   0.0f, 0.0f, 0.0f, 1.0f, 0.0f,
   0.2f, 0.2f, 0.2f, 0.0f, 1.0f};
   
imageAttributes.SetColorMatrix(
   &colorMatrix, 
   ColorMatrixFlagsDefault,
   ColorAdjustTypeBitmap);
   
graphics.DrawImage(&image, 10, 10);

graphics.DrawImage(
   &image, 
   Rect(120, 10, width, height),  // destination rectangle 
   0, 0,        // upper-left corner of source rectangle 
   width,       // width of source rectangle
   height,      // height of source rectangle
   UnitPixel,
   &imageAttributes);

A ilustração a seguir mostra a imagem original à esquerda e a imagem transformada à direita.

O código no exemplo anterior usa as seguintes etapas para executar a recoloração:

1. Inicializar uma estrutura ColorMatrix .
2. Crie um objeto ImageAttributes e passe o endereço da estrutura ColorMatrix para o método ImageAttributes::SetColorMatrix do objeto ImageAttributes .
3. Passe o endereço do objeto ImageAttributes para o método DrawImage Methods de um objeto Graphics .