Avaliar função de probabilidade
Importante
O suporte para o Machine Learning Studio (clássico) terminará em 31 de agosto de 2024. É recomendável fazer a transição para o Azure Machine Learning até essa data.
A partir de 1º de dezembro de 2021, você não poderá criar recursos do Machine Learning Studio (clássico). Até 31 de agosto de 2024, você pode continuar usando os recursos existentes do Machine Learning Studio (clássico).
- Confira informações sobre como mover projetos de machine learning do ML Studio (clássico) para o Azure Machine Learning.
- Saiba mais sobre o Azure Machine Learning.
A documentação do ML Studio (clássico) está sendo desativada e pode não ser atualizada no futuro.
Ajusta uma função de distribuição de probabilidade especificada para um conjunto de dados
Categoria: Funções Estatísticas
Observação
Aplica-se a: somente Machine Learning Studio (clássico)
Módulos semelhantes do tipo "arrastar e soltar" estão disponíveis no designer do Azure Machine Learning.
Visão geral do módulo
Este artigo descreve como usar o módulo Avaliar Função de Probabilidade no Machine Learning Studio (clássico), para calcular medidas estatísticas que descrevem a distribuição de uma coluna, como as distribuições Bernoulli, Pareto ou Poisson.
Para usar esse modelo, conecte um conjunto de dados que contém pelo menos uma coluna de valores numéricos e escolha uma distribuição de probabilidade para testar. O módulo retorna uma tabela de dados que contém valores da função de probabilidade especificada.
Você pode calcular qualquer um desses valores para a distribuição de probabilidade escolhida:
- função de distribuição cumulativa (cdf)
- função de distribuição cumulativa inversa (InverseCdf)
- Função de densidade de probabilidade (Pdf)
Por que a distribuição de probabilidade é útil?
Ao avaliar seus dados em relação a uma distribuição de probabilidade, você está mapeando valores de coluna em relação a um conjunto de valores com propriedades conhecidas. Ao saber se seus dados correspondem a uma dessas distribuições conhecidas, você poderá inferir outras propriedades de seus dados. Em geral, você pode obter melhores previsões de um modelo quando você pode identificar a distribuição que melhor atenda os dados.
A questão de qual probabilidade a função de distribuição usa depende dos dados e das variáveis que estão sendo avaliados. Por exemplo, algumas distribuições são projetadas para descrever probabilidades de valores discretos; outros se destinam a uso apenas com variáveis numéricas contínuas. Para algumas distribuições, você também deve saber antecipadamente uma média esperada, graus de liberdade e assim por diante. Para obter detalhes, consulte Distribuições de Probabilidade Com Suporte
Como configurar a Função Avaliar Probabilidade
Todas as opções mudam dependendo do tipo de distribuição de probabilidade que você deseja calcular. Se você alterar o método de distribuição de probabilidade, outras seleções que você pode ter feito serão redefinidas.
Portanto, escolha a opção Distribuição primeiro!
O conjunto de dados usado como entrada deve conter dados numéricos. Outros tipos de dados são ignorados.
Para cada análise, você pode aplicar um único método de distribuição de probabilidade. Para calcular uma distribuição de probabilidade diferente, adicione uma instância separada do módulo para cada distribuição que você pretende testar.
Adicione o módulo Avaliar Função de Probabilidade ao experimento. Você pode encontrar este módulo na categoria Funções Estatísticas no Machine Learning Studio (clássico).
Conexão um conjunto de dados que contém pelo menos uma coluna de números.
Use a opção Distribuição para selecionar o tipo de distribuição de probabilidade que você deseja calcular. Consulte distribuições de probabilidade com suporte para obter uma lista de opções e seus argumentos necessários.
Defina os parâmetros que são necessários para a distribuição.
Escolha uma das três estatísticas a serem criadas: a função de distribuição cumulativa (cdf), a função de distribuição cumulativa inversa (InverseCdf) ou a função de densidade de probabilidade (pdf).
Consulte a seção Notas técnicas para obter definições.
Use o seletor de coluna para escolher as colunas sobre as quais calcular a distribuição de probabilidade selecionada.
Todas as colunas selecionadas devem ter um tipo de dados numérico.
O intervalo de dados na coluna deve também ser válido, tendo em conta a função de probabilidade selecionada. Caso contrário, pode ocorrer um erro ou o resultado NaN.
Para colunas esparsas, os valores que correspondem aos zeros em segundo plano não são processados.
Use a opção modo Resultado para especificar como gerar os resultados. Você pode substituir valores de coluna com os valores de distribuição de probabilidade, acrescentar novos valores ao conjunto de dados ou retornar somente os valores de distribuição de probabilidade.
Execute o experimento ou clique com o botão direito do mouse no módulo Avaliar Função de Probabilidade e clique em Executar selecionado.
Resultados
A tabela a seguir contém um exemplo de resultados, usando a opção Acrescentar , em uma única coluna de temperatura do conjunto de dados de exemplo de Incêndios Florestais .
| temp | StandardNormal.Cdf(temp) | StandardNormal.Pdf(temp) | FFisher.cdf(temp | FFisher.cdf(temp |
|---|---|---|---|---|
| 8.2 | 1 | 1 | 0.984774 | 0.004349 |
| 18 | 1 | 1 | 0.997896 | 0.000311 |
| 14.6 | 1 | 1 | 0.996352 | 0.000648 |
| 8.3 | 1 | 1 | 0.985201 | 0.004187 |
| 11,4 | 1 | 1 | 0.993147 | 0.001502 |
Os títulos das colunas geradas contêm a distribuição de probabilidade usada.
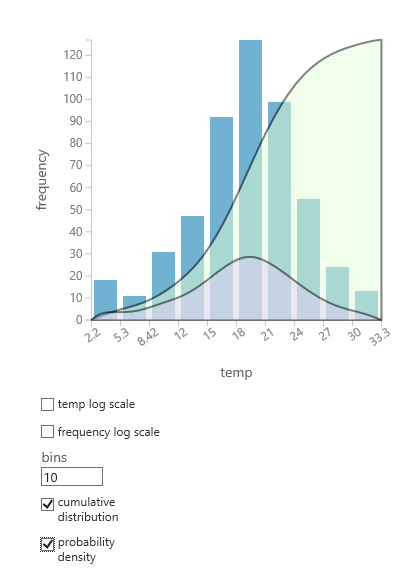
Se você não tiver certeza de qual distribuição de probabilidade provavelmente se adequará aos seus dados, poderá criar um gráfico rápido de distribuição cumulativa e densidade de probabilidade para qualquer coluna numérica.
- Clique com o botão direito do mouse na saída do conjunto de dados ou do módulo e selecione Visualizar.
- Selecione a coluna de interesse e, no painel Histograma , selecione distribuição cumulativa ou densidade de probabilidade.
- Um gráfico da distribuição, como o seguinte, é sobreposto ao histograma que representa os dados.
Distribuições de probabilidade com suporte
O módulo Avaliar Função de Probabilidade dá suporte às seguintes distribuições:
Bernoulli
A distribuição bernoulli é uma distribuição sobre valores binários: em outras palavras, ela modela a distribuição esperada quando apenas dois valores são possíveis.
Para calcular, selecione Bernoulli e defina as seguintes opções:
- Probabilidade de sucesso
O parâmetro p especifica a probabilidade de que um 1 seja gerado. Digite um número (float) entre 0,0 e 1,0 que especifique a probabilidade de sucesso. O padrão é .5.
Beta
A distribuição Beta é uma distribuição monovariável contínua.
Para calcular, selecione Beta e defina as seguintes opções:
Forma
Digite um valor para alterar a forma da distribuição.Um parâmetro de forma é qualquer parâmetro de uma distribuição de probabilidade que define sua localização ou dimensionamento. Portanto, quando você inserir um valor para a forma, o parâmetro altera a forma da distribuição em vez de mover, aumentar ou diminuí-la.
O valor deve ser um número (
double). O padrão é 1.0.Escala
Digite um número para usar no dimensionamento da distribuição.Aplicando um valor de dimensionamento para a distribuição, você pode dimuir ou aumentar.
O valor padrão é 1.0. Os valores devem ser números positivos.
Limite superior
Digite um número (double) que represente o limite superior da distribuição. O padrão é 1.0.Limite inferior
Digite um número (double) que represente o limite inferior da distribuição. O padrão é 0.0.
Binomial
A distribuição binomial é uma distribuição univariada discreta. A distribuição binomial é usada para modelar o número de sucessos em uma amostra. A substituição é usada durante a amostragem. Para amostragem sem substituição, use a Distribuição hipergeométrica.
Para calcular, selecione Binomial e defina as seguintes opções:
Probabilidade de sucesso
Digite um número (float) entre 0,0 e 1,0 que indique a probabilidade de sucesso. O padrão é .5.Número de tentativas
Especifique o número de tentativas.Use um
integer, com um valor mínimo de 1. O padrão é 3.
Cauchy
A distribuição Cauchy é uma distribuição de probabilidade contínua simétrica.
Para calcular, selecione Cauchy e defina as seguintes opções:
Localidade
Digite um número (double) que representa o local do0º elemento.Especificando um valor para o parâmetro local, você pode alterar a distribuição de probabilidade para cima ou para baixo em uma escala numérica.
O padrão é 0.0.
ChiSquare
A distribuição qui-quadrado é uma soma dos quadrados de k variáveis independentes, padrão, normais e aleatórias.
Para calcular, selecione ChiSquare e defina as seguintes opções:
- Número de graus de liberdade Digite um número (
double) para especificar os graus de liberdade. O padrão é 1.0.
ChiSquareRightTailed
Essa opção fornece uma distribuição qui-quadrado com cauda direita.
Para calcular, selecione ChiSquareRightTailed e defina as seguintes opções:
- Número de graus de liberdade
Digite um número (double) para especificar os graus de liberdade. O padrão é 1.0.
Exponencial
A distribuição exponencial é uma distribuição nos números reais parametrizados por um parâmetro não negativo.
Para calcular, selecione Exponencial e defina as seguintes opções:
- Lambda
Digite um número (double) para usar como o parâmetro lambda. O padrão é 1.0.
FFisher
Gera a probabilidade da estatística Fisher para uma amostra, também conhecida como distribuição F do Fisher. Essa distribuição é bicaudal.
Para calcular, selecione FFisher e defina as seguintes opções:
Graus de liberdade do numerador
Digite um número (double) para especificar os graus de liberdade usados no numerador. O padrão é 3.0.Graus de liberdade do denominador
Digite um número (double) para especificar os graus de liberdade usados no denominador. O padrão é 6.0.
FFisherRightTailed
Cria uma distribuição fisher com cauda direita. A distribuição de Fisher é também conhecida como a distribuição Fisher F, distribuição de Snedecor ou distribuição Fisher Snedecor. Esse forma particular da distribuição é de cauda direita.
Para calcular, selecione FFisherRightTailed e defina as seguintes opções:
Graus de liberdade do numerador
Digite um número (double) para especificar os graus de liberdade usados no numerador. O padrão é 3.0.Graus de liberdade do denominador
Digite um número (double) para especificar os graus de liberdade usados no denominador. O padrão é 6.0.
Gama
A distribuição gama é uma família de distribuições de probabilidade contínua com dois parâmetros. Por exemplo, qui-quadrado é um caso especial da distribuição gama.
Para calcular, selecione Gama e defina as seguintes opções:
Escala
Digite um valor para usar no dimensionamento da distribuição.Aplicando um valor de dimensionamento para a distribuição, você pode dimuir ou aumentar.
O valor padrão é 1.0. Os valores devem ser números positivos.
Localidade
Digite um número (double) que representa o local do0º elemento.Especificando um valor para o parâmetro local, você pode alterar a distribuição de probabilidade para cima ou para baixo em uma escala numérica.
O padrão é 0.0.
GeneralizedExtremeValues
Cria uma distribuição desenvolvida para lidar com valores extremos. A distribuição de valor extremo generalizado (GEV) é atualmente um grupo de distribuições de probabilidade contínua que combina as distribuições Gumbel, Fréchet e Weibull (também conhecidas como distribuições de valor extremo do tipo I, II e III).
Para obter mais informações sobre a teoria do valor extremo, consulte este artigo na Wikipédia: teorema Fisher-Tippet-Gnedenko.
Para calcular, selecione GeneralizedExtremeValues e defina as seguintes opções:
Forma
Digite um valor para alterar a forma da distribuição.Um parâmetro de forma é qualquer parâmetro de uma distribuição de probabilidade que define sua localização ou dimensionamento. Portanto, quando você inserir um valor para a forma, o parâmetro altera a forma da distribuição em vez de mover, aumentar ou diminuí-la.
O valor deve ser um número (
double). O padrão é 1.0.Escala
Digite um valor para usar no dimensionamento da distribuição.Aplicando um valor de dimensionamento para a distribuição, você pode dimuir ou aumentar.
O valor padrão é 1.0. Os valores devem ser números positivos.
Localidade
Digite um número (double) que representa o local do0º elemento.Ao digitar um valor para o parâmetro local, você pode alterar a distribuição de probabilidade para cima ou para baixo em uma escala numérica.
O padrão é 0.0.
Geométrico
A distribuição geométrica é uma distribuição sobre inteiros positivos parametrizados por um número real positivo.
Para calcular, selecione Geométrico e defina as seguintes opções:
- Probabilidade de sucesso
Digite um número (float) entre 0,0 e 1,0 que indique a probabilidade de sucesso. O padrão é .5.
Observação
Essa implementação da distribuição geométrica não gera zeros.
GumbelMax
A distribuição Gumbel é uma dentre várias distribuições de valor extremo. A opção GumbelMax implementa a distribuição Valor Extremo Máximo Tipo 1.
Para calcular, selecione GumbelMax e defina as seguintes opções:
Escala
Digite um valor para usar no dimensionamento da distribuição.Aplicando um valor de dimensionamento para a distribuição, você pode dimuir ou aumentar.
O valor padrão é 1.0. Os valores devem ser números positivos.
Localidade
Digite um número (double) que representa o local do0º elemento.Ao digitar um valor para o parâmetro local, você pode alterar a distribuição de probabilidade para cima ou para baixo em uma escala numérica.
O padrão é 0.0.
GumbelMin
A distribuição Gumbel é uma dentre várias distribuições de valor extremo. A distribuição Gumbel também é conhecida como a distribuição de valor extremo menor (SEV) ou a distribuição de valor extremo menor (Tipo I). A opção GumbelMin implementa a distribuição mínimo de valor extremo tipo 1.
Para calcular, selecione GumbelMin e defina as seguintes opções:
Escala
Digite um valor para usar no dimensionamento da distribuição.Aplicando um valor de dimensionamento para a distribuição, você pode dimuir ou aumentar.
O valor padrão é 1.0. Os valores devem ser números positivos.
Localidade
Digite um número (double) que representa o local do0º elemento.Ao digitar um valor para o parâmetro local, você pode alterar a distribuição de probabilidade para cima ou para baixo em uma escala numérica.
O padrão é 0.0.
Hipergeométrica
A distribuição hipergeométrica é uma distribuição de probabilidade discreta que descreve o número de êxitos em uma sequência de n extrai de uma população finita sem substituição, assim como a distribuição binomial descreve o número de êxitos para sorteios com substituição.
Para calcular, selecione Hypergeometric e defina as seguintes opções:
Número de exemplos
Digite um número inteiro que indica o número de amostras a serem usadas. O padrão é 9.Número de sucesso
Digite um número inteiro que defina o valor de sucesso. O padrão é 24.Tamanho da população
Especifique o tamanho da população a ser usado ao calcular a distribuição hipergeométrica.
Laplace
A distribuição laplace é uma distribuição sobre os números reais, parametrizada por uma média e por um parâmetro de escala.
Para calcular, selecione a distribuição do Laplace e defina as seguintes opções:
Escala
Digite um valor para usar no dimensionamento da distribuição.Aplicando um valor de dimensionamento para a distribuição, você pode dimuir ou aumentar.
O valor padrão é 1.0. Os valores devem ser números positivos.
Localidade
Digite um número (double) que representa o local do0º elemento.Ao digitar um valor para o parâmetro local, você pode alterar a distribuição de probabilidade para cima ou para baixo em uma escala numérica.
O padrão é 0.0.
Logística
A distribuição logística é semelhante à distribuição normal, mas não tem um limite no lado esquerdo da distribuição. A distribuição logística é usada em modelos de rede neural e regressão logística e para modelar dados de ciências da vida.
Para calcular, selecione Logística e defina as seguintes opções:
Escala
Digite um valor para usar no dimensionamento da distribuição.Aplicando um valor de dimensionamento para a distribuição, você pode dimuir ou aumentar.
O valor padrão é 1.0. Os valores devem ser números positivos.
Mean
Digite um número (double) que indique o valor médio estimado da distribuição. O padrão é 0.0.
Lognormal
A distribuição lognormal é uma distribuição monovariável contínua.
Para calcular, selecione Lognormal e defina as seguintes opções:
Mean
Digite um número (double) que indica o valor médio estimado da distribuição. O padrão é 0.0.Desvio padrão
Digite um número positivo (double) que indique o desvio padrão estimado da distribuição. O padrão é 1.0.
NegativeBinomial
A distribuição binomial negativa é uma distribuição nos números naturais com dois parâmetros (r, p). No caso especial que r é um inteiro, você pode interpretar a distribuição como o número de caudas antes da cabeça rth quando a probabilidade da cabeça é p.
Para calcular, selecione NegativeBinomial e defina as seguintes opções:
Probabilidade de sucesso
Digite um número (float) entre 0,0 e 1,0 que indique a probabilidade de sucesso. O padrão é .5.Número de sucesso
Digite um número inteiro que especifique o valor de sucesso. O padrão é 24.
Normal
A distribuição normal também é conhecida como distribuição gaussiana.
Para calcular, selecione Normal e defina as seguintes opções:
Mean
Digite um número (double) que indica o valor médio estimado da distribuição. O padrão é 0.0.Desvio padrão
Digite um número positivo (double) que indique o desvio padrão estimado da distribuição. O padrão é 1.0.
Pareto
A distribuição Pareto é uma distribuição de probabilidade de lei de energia que coincide com os tipos social, científico, geofísico, atuarial e muitos outros tipos de fenômenos observáveis.
Para calcular, selecione Pareto e defina as seguintes opções:
Forma
Digite um valor (opcional) para alterar a forma da distribuição.Um parâmetro de forma é qualquer parâmetro de uma distribuição de probabilidade que define sua localização ou dimensionamento. Portanto, quando você inserir um valor para a forma, o parâmetro altera a forma da distribuição em vez de mover, aumentar ou diminuí-la.
O valor deve ser um número (
double). O padrão é 1.0.Escala
Digite um valor (opcional) para alterar a escala da distribuição. Aplicando um valor de dimensionamento para a distribuição, você pode dimuir ou aumentar.O valor deve ser um número (
double). O padrão é 1.0.
Poisson
Nessa implementação, o método de Knuth é usado para gerar variáveis aleatórias distribuídas de Poisson. Para obter mais informações sobre a distribuição Poisson, consulte Regressão de Poisson.
Para calcular, selecione Poisson e defina as seguintes opções:
- Mean
Digite um número (double) que indica o valor médio estimado da distribuição. O padrão é 0.0.
Rayleigh
A distribuição de Rayleigh é uma distribuição de probabilidade contínua. Como um exemplo de como ela ocorre, a velocidade do vento terá uma distribuição Rayleigh se os componentes do vetor de velocidade do vento bidimensional forem não correlacionados e normalmente distribuídos com variância igual.
Para calcular, selecione Rayleigh e defina as seguintes opções:
- Limite inferior
Digite um número (double) que represente o limite inferior da distribuição. O padrão é 0.0.
StandardNormal
Essa opção fornece a distribuição normal padrão, sem outros parâmetros.
Para calcular, selecione StandardNormal e selecione as colunas.
TStudent
Essa opção implementa a distribuição t do Student univariada.
Para calcular, selecione TStudent e defina as seguintes opções:
- Número de graus de liberdade
Digite um número (double) para especificar os graus de liberdade. O padrão é 1.0.
TStudentRightTailed
Implementa a distribuição T do Student monovariável usando uma cauda direita.
Para calcular, selecione TStudentRightTailed e defina as seguintes opções:
- Número de graus de liberdade
Digite um número (double) para especificar os graus de liberdade. O padrão é 1.0.
TStudentTwoTailed
Implementa uma distribuição T do Student de bicaudal.
Para calcular, selecione TStudentTwoTailed e defina as seguintes opções:
- Número de graus de liberdade
Digite um número (double) para especificar os graus de liberdade. O padrão é 1.0.
Uniforme
A distribuição uniforme também é conhecida como distribuição retangular.
Para calcular, selecione Uniform e defina as seguintes opções:
Limite inferior
Digite um número (double) que represente o limite inferior da distribuição. O padrão é 0.0.Limite superior
Digite um número (double) que represente o limite superior da distribuição. O padrão é 1.0.
Weibull
A distribuição Weibull é amplamente usada na engenharia de confiabilidade. Você pode usar seu parâmetro Shape para modelar muitas outras distribuições.
Para calcular, selecione Weibull e defina as seguintes opções:
Forma
Digite um valor (opcional) para alterar a forma da distribuição.Um parâmetro de forma é qualquer parâmetro de uma distribuição de probabilidade que define sua localização ou dimensionamento. Portanto, quando você inserir um valor para a forma, o parâmetro altera a forma da distribuição em vez de mover, aumentar ou diminuí-la.
O valor deve ser um número (
double). O padrão é 1.0.Escala
Digite um valor (opcional) para alterar a escala da distribuição. Aplicando um valor de dimensionamento para a distribuição, você pode dimuir ou aumentar.O valor deve ser um número (
double). O padrão é 1.0.
Observações técnicas
Esta seção contém detalhes de implementação, dicas e respostas para perguntas frequentes.
Detalhes de implementação
Este módulo oferece suporte a todas as distribuições que são fornecidas na biblioteca MATH.NET Numerics de software livre. Para obter mais informações, consulte a documentação da biblioteca Math.Net.Numerics.Distribution .
As distribuições de cauda direita e duas caudas aparecem como distribuições separadas, não como versões parametrizadas de distribuições base. O comportamento atual é preservar a compatibilidade com o Excel.
Definições
Este módulo dá suporte ao cálculo de qualquer um desses valores para a distribuição especificada:
cdf ou a função de distribuição cumulativa
Retorna a probabilidade de um evento composto, definido como a soma das ocurrências quando a variável aleatória leva um valor menor que algum valor específico x.
Em outras palavras, ele responde à pergunta: "Quão comuns são exemplos que são menores ou iguais a esse valor?"
Essa função pode ser usada com variáveis numéricas contínuas e discretas.
InverseCdf ou a função de distribuição cumulativa inversa
Retorna o valor associado a um valor de probabilidade cumulativo específico (cdf).
Em outras palavras, ele responde à pergunta: "Qual é o valor de x no qual a função cdf retorna a probabilidade cumulativa y?"
pdf ou a função de densidade de probabilidade
Descreve a probabilidade relativa de uma variável aleatória ser um valor específico.
Em outras palavras, ele responde à pergunta: "Quão comuns são as amostras exatamente neste valor?"
Entradas esperadas
| Nome | Tipo | Descrição |
|---|---|---|
| Dataset | Tabela de Dados | Conjunto de dados de entrada |
Parâmetros do módulo
| Nome | Intervalo | Type | Padrão | Descrição |
|---|---|---|---|---|
| Distribuição | Qualquer | ProbabilityDistribution | StandardNormal | Selecione o tipo de distribuição de probabilidade para gerar. |
| Método | Qualquer | ProbabilityDistributionMethod | Cdf | Selecione o método a ser usado ao calcular a distribuição de probabilidade selecionada. As opções são a função de distribuição cumulativa (cdf), a função de distribuição cumulativa inversa (InverseCdf) e a função de densidade de probabilidade ou a função em massa (pdf). |
| Método de distribuição binomial negativa | Qualquer | ProbabilityDistributionMethodForNegativeBinomial | Cdf | Se você selecionar a distribuição binomial negativa, especifique o método usado para avaliar a distribuição. |
| Probabilidade de sucesso | [0,0;1,0] | Float | 0,5 | Digite um valor para usar como a probabilidade de sucesso. |
| Forma | Qualquer | Float | 1.0 | Digite um valor que modifique a forma da distribuição. |
| Escala | >=0,0 | Float | 1.0 | Digite um valor que altere a escala da distribuição, para expandir ou reduzir o tamanho. |
| Número de tentativas | >=1 | Integer | 3 | Especifique o número de tentativas. |
| Limite inferior | Qualquer | Float | 0,0 | Digite um número a ser usado como o limite inferior da distribuição |
| Limite superior | Qualquer | Float | 1.0 | Digite um número a ser usado como o limite superior da distribuição |
| Location | Qualquer | Float | 0,0 | Digite o local do elemento zero na distribuição. |
| Número de graus de liberdade | Qualquer | Float | 1.0 | Especifique o número de graus de liberdade. |
| Graus de liberdade do numerador | Qualquer | Float | 3.0 | Especifique o número de graus de liberdade no numerador. |
| Graus de liberdade do denominador | Qualquer | Float | 6,0 | Especifique o número de graus de liberdade no denominador. |
| Lambda | >=0,0 | Float | 1.0 | Especifique um valor para o parâmetro Lambda. |
| Número de amostras | Qualquer | Integer | 9 | Especifique o número de amostras. |
| Número de sucesso | Qualquer | Integer | 24 | Digite um valor a ser usado como o número de sucesso. |
| Tamanho da população | Qualquer | Integer | 52 | Especifique o tamanho da população. |
| Média | Qualquer | Float | 0,0 | Digite o valor médio estimado. |
| Desvio padrão | >=0,0 | Float | 1.0 | Digite o desvio padrão estimado. |
| Conjunto de colunas | Qualquer | ColumnSelection | Escolha as colunas sobre as quais calcular a distribuição de probabilidade. | |
| Modo de resultado | Qualquer | OutputTo | ResultOnly | Especifica como os resultados serão salvos no conjunto de dados de saída. As opções são acrescentar novas colunas, substituir as colunas existentes ou produzir apenas os resultados. |
Saída
| Nome | Tipo | Descrição |
|---|---|---|
| Conjunto de dados de resultados | Tabela de Dados | Conjunto de dados de saída |
Exceção
Para obter uma lista completa de mensagens de erro, consulte Códigos de Erro do Módulo.
| Exceção | Descrição |
|---|---|
| Erro 0017 | Ocorre uma exceção se uma ou mais colunas especificadas tem um tipo que não é suportado pelo módulo atual. |
Para obter uma lista de erros específicos aos módulos do Studio (clássico), consulte Machine Learning códigos de erro.
Para obter uma lista de exceções de API, consulte Machine Learning códigos de erro da API REST.