Hipoteza testowa przy użyciu testu t
Ważne
Obsługa programu Machine Learning Studio (wersja klasyczna) zakończy się 31 sierpnia 2024 r. Zalecamy przejście do usługi Azure Machine Learning przed tym terminem.
Od 1 grudnia 2021 r. nie będzie można tworzyć nowych zasobów programu Machine Learning Studio (wersja klasyczna). Do 31 sierpnia 2024 r. można będzie nadal korzystać z istniejących zasobów programu Machine Learning Studio (wersja klasyczna).
- Zobacz informacje na temat przenoszenia projektów uczenia maszynowego z programu ML Studio (wersja klasyczna) do Azure Machine Learning.
- Dowiedz się więcej o Azure Machine Learning.
Dokumentacja programu ML Studio (wersja klasyczna) jest wycofywana i może nie być aktualizowana w przyszłości.
Porównuje średnich z dwóch kolumn przy użyciu testu t
Kategoria: Funkcje statystyczne
Uwaga
Dotyczy: tylko Machine Learning Studio (wersja klasyczna)
Podobne moduły przeciągania i upuszczania są dostępne w projektancie Azure Machine Learning.
Omówienie modułu
W tym artykule opisano sposób użycia modułu Test Hypothesis Using t-Test w programie Machine Learning Studio (wersja klasyczna), aby wygenerować wyniki dla trzech typów testów t:
- Pojedynczy przykładowy test t
- Sparowany test t
- Niespłacony test t
Ogólnie rzecz biorąc, test t pomaga porównać, czy dwie grupy mają różne środki. Załóżmy na przykład, że oceniasz dane z badań dla pacjentów, którzy otrzymali lek A, a pacjenci, którzy otrzymali lek B, i należy porównać metrykę współczynnika odzyskiwania dla obu grup. Hipoteza zerowa zakładałaby, że wskaźnik odzyskiwania jest taki sam w obu grupach, a ponadto, że wartości współczynnika odzyskiwania mają normalny rozkład w obu grupach.
Używając hipotezy testowej przy użyciu funkcji t-Test i podając kolumny zawierające współczynniki odzyskiwania jako dane wejściowe, można uzyskać wyniki wskazujące, czy różnica jest znacząca, co oznacza, że hipoteza zerowa powinna zostać odrzucona. Test uwzględnia czynniki, takie jak wielkość różnicy między wartościami, rozmiarem próbki (większym jest lepsze) i wielkością odchylenia standardowego (niższym jest lepsze).
Przeglądając wyniki modułu Test Hypothesis Using t-Test (Hipoteza testowa przy użyciu t-Test ), można określić, czy hipoteza zerowa ma wartość TRUE czy FALSE, i przejrzeć wyniki ufności (P) z testu t.
Jak wybrać test t
Wybierz pojedynczy test t-testowy, gdy mają zastosowanie następujące warunki:
Masz jedną próbkę wyników.
Wszystkie wyniki są niezależne od siebie.
Rozkład próbkowania xˉ jest normalny.
Ogólnie rzecz biorąc, pojedynczy test t-próbki służy do porównywania wartości średniej ze znaną liczbą.
Wybierz sparowany test t,gdy mają zastosowanie następujące warunki:
Masz dopasowane pary wyników. Na przykład możesz mieć dwie różne miary na osobę lub dopasowane pary osób (takich jak mąż i żona).
Każda para wyników jest niezależna od każdej innej pary.
Rozkład próbkowania d jest normalny.
Sparowany test t jest przydatny podczas porównywania powiązanych przypadków. Uśredniając różnice między wynikami sparowanych przypadków, można określić, czy łączna różnica jest statystycznie znacząca.
Wybierz niespłacony test t, gdy mają zastosowanie następujące warunki:
Masz dwa niezależne próbki wyników. Oznacza to, że nie ma podstaw do parowania wyników w próbce 1 z tymi w próbie 2.
Wszystkie wyniki w próbce są niezależne od wszystkich innych wyników w ramach tej próbki.
Rozkład próbkowania x1-x2 jest normalny.
Opcjonalnie należy spełnić wymaganie, aby wariancja między grupami była w przybliżeniu równa.
Jak skonfigurować hipotezę testową przy użyciu testu t-Test
Użyj pojedynczego zestawu danych jako danych wejściowych. Porównywane kolumny muszą znajdować się w tym samym zestawie danych.
Jeśli musisz porównać kolumny z różnych zestawów danych, możesz wyizolować każdą kolumnę do porównania przy użyciu pozycji Wybierz kolumny w zestawie danych, a następnie scalić je z jednym zestawem danych przy użyciu polecenia Dodaj kolumny.
Dodaj do eksperymentu moduł Hipoteza testowa przy użyciu narzędzia t-Test .
Ten moduł można znaleźć w kategorii Funkcje statystyczne w programie Studio (wersja klasyczna).
Dodaj zestaw danych zawierający kolumnę lub kolumny, które chcesz przeanalizować.
Zdecyduj, jakiego rodzaju test t jest odpowiedni dla Twoich danych. Zobacz Jak wybrać test t..
Pojedynczy przykład: jeśli używasz pojedynczego przykładu, ustaw następujące parametry:
Hipoteza zerowa μ: wpisz wartość, która ma być używana jako średnia hipoteza zerowa dla próbki. Określa oczekiwaną wartość średnią, względem której będzie testowana średnia z próby.
Kolumna docelowa: użyj selektora kolumn, aby wybrać jedną kolumnę liczbową na potrzeby testowania.
Typ hipotezy: wybierz test z jednym lub dwoma ogonami. Wartość domyślna to test dwuogonowy. Jest to najbardziej typowy typ testu, w którym oczekiwany rozkład jest symetryczny wokół zera.
Opcja One Tail GT jest dostępna dla jednego ogona większego niż test. Ten test daje większą moc do wykrywania efektu w jednym kierunku, nie testując efektu w drugim kierunku.
Opcja One Tail LT daje jednoogonową wartość mniejszą niż test.
α: określ współczynnik ufności. Ta wartość jest używana do oceny wartości P (pierwsze dane wyjściowe modułu). Jeśli p jest niższy niż współczynnik ufności, hipoteza zerowa zostanie odrzucona.
PairedSamples: Jeśli porównujesz dwie próbki z tej samej populacji, ustaw następujące parametry:
Hipoteza zerowa μ: wpisz wartość reprezentującą różnicę próbek między parą próbek.
Kolumna docelowa: użyj selektora kolumn, aby wybrać dwie kolumny liczbowe do przetestowania.
Typ hipotezy: wybierz test z jednym lub dwoma ogonami. Wartość domyślna to test dwuogonowy.
α: określ współczynnik ufności. Ta wartość służy do oceny wartości P (pierwsze dane wyjściowe modułu)> Jeśli wartość p jest niższa niż współczynnik ufności, hipoteza zerowa zostanie odrzucona.
Niespłacone próbki: jeśli porównasz dwa niespłacone próbki, ustaw następujące parametry:
- Przyjmij równą wariancję: Usuń zaznaczenie tej opcji, gdy próbki pochodzą z różnych populacji.
- Hipoteza zerowa μ1: wpisz średnią dla pierwszej kolumny.
- Hipoteza zerowa μ2: wpisz średnią dla drugiej kolumny.
- Kolumny docelowe: użyj selektora kolumn, aby wybrać dwie kolumny liczbowe do przetestowania.
- Typ hipotezy: wskazuje, czy test jest jedno-ogonowy, czy dwuogonowy. Wartość domyślna to test dwuogonowy.
- α: określ współczynnik ufności. Ta wartość służy do oceny wartości P (pierwsze dane wyjściowe modułu)> Jeśli wartość p jest niższa niż współczynnik ufności, hipoteza zerowa zostanie odrzucona.
Uruchom eksperyment.
Wyniki
Dane wyjściowe modułu to zestaw danych zawierający wyniki testu t i przekształcenie, które można opcjonalnie zapisać w celu ponownego zastosowania tego lub innego zestawu danych przy użyciu funkcji Zastosuj przekształcenie.
Zestaw danych wyników zawiera te wartości, niezależnie od typu użytego testu t:
- Wynik prawdopodobieństwa wskazujący pewność hipotezy zerowej
- Wartość wskazująca, czy hipoteza zerowa powinna zostać odrzucona
Porada
Pamiętaj, że celem jest ustalenie, czy można odrzucić hipotezę zerową. Wynik 0 nie oznacza, że należy zaakceptować hipotezę zerową: oznacza to, że nie masz wystarczającej ilości danych i potrzebujesz dalszych badań.
Uwagi techniczne
Moduł automatycznie nazywa kolumny wyjściowe zgodnie z poniższymi konwencjami, w zależności od wybranego typu testu t i tego, czy wynik miał zostać odrzucony, czy zaakceptowany hipoteza zerowa.
Nadane kolumny wejściowe o nazwach {0} i {1}, moduł tworzy następujące nazwy:
| Kolumny | SingleSampleSet | Sparowane próbki | Niespłacone próbki |
|---|---|---|---|
| Kolumna wyjściowa P | P_ss({0}) | P_ps({0}, {1}) | P_us({0}, {1}) |
| Odrzuć kolumnę wyjściowąH0 | RejectH0_ss({0})" | RejectH0_ps({0}, {1}) | RejectH0_us({0}, {1}) |
Sposób obliczania wyników
Ten moduł oblicza i używa przykładowego odchylenia standardowego; w związku z tym równanie jest używane (n-1) w mianowniku.
Wyniki obliczeń dla pojedynczego przykładowego testu
Biorąc pod uwagę pojedynczą próbkę wyników, wszystkie niezależnie od siebie i rozkład normalny, wynik jest obliczany w następujący sposób:
Weź następujące dane wejściowe:
- Pojedyncza kolumna wartości z zestawu danych
- Hipoteza zerowa (H0) parametr μ0
- Wskaźnik ufności określony przez α
Wyodrębnij liczbę próbek (n).
Oblicz średnią przykładowych danych.
Oblicz odchylenie standardowe (s) przykładowych danych.
Oblicz stopień swobody (df):
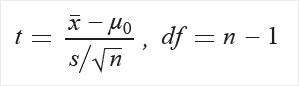
Wyodrębnij prawdopodobieństwo P z tabeli dystrybucji T przy użyciu t i df.
Wyniki obliczeń dla sparowanego testu t-testowego
Biorąc pod uwagę dopasowany zestaw wyników, z każdą parą niezależną od drugiej i rozkład normalny w każdym zestawie, wynik jest obliczany w następujący sposób:
Weź następujące dane wejściowe:
- Dwie kolumny wartości z zestawu danych
- Hipoteza zerowa (H0) parametr d0
- Wskaźnik ufności określony przez α
Wyodrębnij pewną liczbę par próbek (n).
Oblicz średnią różnic dla przykładowych danych:
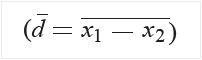
Oblicz odchylenie standardowe różnic (sd).
Oblicz stopień swobody (df):
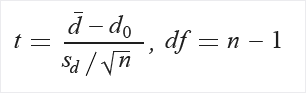
Wyodrębnij prawdopodobieństwo (P) z tabeli dystrybucji (T) przy użyciu języka t i df.
Wyniki obliczeń dla niespłaconego testu t-testowego
Biorąc pod uwagę dwie niezależne próbki wyników, z normalnym rozkładem wartości w każdej próbce, wynik jest obliczany w następujący sposób:
Weź następujące dane wejściowe:
- Zestaw danych zawierający dwie kolumny
doubles - Parametr hipotezy zerowej (H0) (d0)
- Wskaźnik ufności określony przez α
- Zestaw danych zawierający dwie kolumny
Wyodrębnij kilka próbek w każdej grupie, n1 i n2.
Oblicz metodę dla każdego z zestawów próbek.
Oblicz odchylenie standardowe dla każdej grupy jako s1 i s2.
Oblicz stopień swobody (df):
Opcjonalnie należy spełnić wymaganie, aby wariancja między grupami byłaby w przybliżeniu równa się w następujący sposób:
Najpierw oblicz odchylenie standardowe w puli:
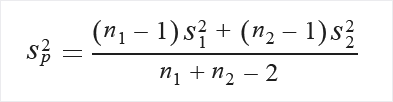
Jeśli nie ma założeń dotyczących równości wariancji, oblicz w następujący sposób:
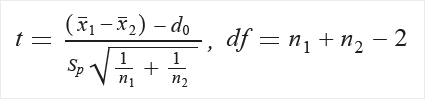
Wyodrębnij P z tabeli dystrybucji (T) przy użyciu języka t i df.
Obliczanie hipotezy zerowej
Prawdopodobieństwo hipotezy zerowej, wyznaczonej jako P, jest obliczane w następujący sposób:
Jeśli α P < , ustaw flagę Odrzuć na wartość True.
Jeśli ≥ α P, ustaw flagę Odrzuć na Wartość Fałsz.
Oczekiwane dane wejściowe
| Nazwa | Typ | Opis |
|---|---|---|
| Zestaw danych | Tabela danych | Wejściowy zestaw danych |
Parametry modułu
| Nazwa | Zakres | Typ | Domyślny | Opis |
|---|---|---|---|---|
| Typ hipotezy | Dowolne | Hipoteza | Dwa ogony | Typ hipotezy zerowej t-testowego ucznia |
| Hipoteza zerowa μ | Dowolne | Float | 0,0 | W przypadku pojedynczego testu t-próbki średnia zerowa dla próbki W przypadku sparowanego testu t-test różnicy przykładowej |
| Kolumny docelowe | Dowolne | KolumnaWybieranie | Brak | Wzorzec wyboru kolumn docelowych |
| Przyjmij równe wariancji | Dowolne | Boolean | Prawda | Przyjmij, że wariancja dwóch próbek jest równa Dotyczy tylko niespłaconych próbek |
| Hipoteza zerowa μ1 | Dowolne | Float | 0,0 | Hipoteza zerowa dla pierwszej próbki |
| Α | [0.0;1.0] | Float | 0,95 | Współczynnik ufności (jeśli wartość P jest niższa niż współczynnik ufności, hipoteza zerowa jest odrzucana) |
Dane wyjściowe
| Nazwa | Typ | Opis |
|---|---|---|
| P | Tabela danych | Wynik prawdopodobieństwa wskazujący pewność hipotezy zerowej |
| Odrzuć H0 | Tabela danych | Wartość wskazująca, czy hipoteza zerowa powinna zostać odrzucona |
Wyjątki
| Wyjątek | Opis |
|---|---|
| Błąd 0003 | Wyjątek występuje, jeśli co najmniej jeden z danych wejściowych ma wartość null lub jest pusty. |
| Błąd 0008 | Wyjątek występuje, jeśli parametr nie znajduje się w zakresie. |
| Błąd 0017 | Wyjątek występuje, jeśli co najmniej jedna określona kolumna ma typ, który nie jest obsługiwany przez bieżący moduł. |
| Błąd 0020 | Wyjątek występuje, jeśli liczba kolumn w niektórych zestawach danych przekazanych do modułu jest za mała. |
| Błąd 0021 | Wyjątek występuje, jeśli liczba wierszy w niektórych zestawach danych przekazanych do modułu jest za mała. |
| Błąd 0031 | Wyjątek występuje, jeśli liczba kolumn w zestawie kolumn jest mniejsza niż wymagana. |
| Błąd 0032 | Wyjątek występuje, jeśli argument nie jest liczbą. |
| Błąd 0033 | Wyjątek występuje, jeśli argument jest nieskończoność. |
Aby uzyskać listę błędów specyficznych dla modułów programu Studio (klasycznych), zobacz Machine Learning Kody błędów.
Aby uzyskać listę wyjątków interfejsu API, zobacz Machine Learning kody błędów interfejsu API REST.