Ocena funkcji prawdopodobieństwa
Ważne
Obsługa programu Machine Learning Studio (wersja klasyczna) zakończy się 31 sierpnia 2024 r. Zalecamy przejście do usługi Azure Machine Learning przed tym terminem.
Od 1 grudnia 2021 r. nie będzie można tworzyć nowych zasobów programu Machine Learning Studio (wersja klasyczna). Do 31 sierpnia 2024 r. można będzie nadal korzystać z istniejących zasobów programu Machine Learning Studio (wersja klasyczna).
- Zobacz informacje na temat przenoszenia projektów uczenia maszynowego z programu ML Studio (wersja klasyczna) do Azure Machine Learning.
- Dowiedz się więcej o Azure Machine Learning.
Dokumentacja programu ML Studio (wersja klasyczna) jest wycofywana i może nie być aktualizowana w przyszłości.
Dopasowuje określoną funkcję rozkładu prawdopodobieństwa do zestawu danych
Kategoria: Funkcje statystyczne
Uwaga
Dotyczy: tylko Machine Learning Studio (wersja klasyczna)
Podobne moduły przeciągania i upuszczania są dostępne w projektancie Azure Machine Learning.
Omówienie modułu
W tym artykule opisano sposób użycia modułu Evaluate Probability Function (Ocena prawdopodobieństwa) w programie Machine Learning Studio (wersja klasyczna), aby obliczyć miary statystyczne opisujące rozkład kolumny, takie jak rozkłady Bernoulli, Pareto lub Poisson.
Aby użyć tego modelu, połącz zestaw danych zawierający co najmniej jedną kolumnę wartości liczbowych i wybierz rozkład prawdopodobieństwa do przetestowania. Moduł zwraca tabelę danych zawierającą wartości z określonej funkcji prawdopodobieństwa.
Dla wybranego rozkładu prawdopodobieństwa można obliczyć dowolną z tych wartości:
- funkcja rozkładu skumulowanego (cdf)
- odwrotna funkcja rozkładu skumulowanego (InverseCdf)
- funkcja gęstości prawdopodobieństwa (Pdf)
Dlaczego rozkład prawdopodobieństwa jest przydatny?
Podczas oceniania danych względem rozkładu prawdopodobieństwa mapujesz wartości kolumn na zestaw wartości ze znanymi właściwościami. Wiedząc, czy dane odpowiadają jednej z tych dobrze znanych dystrybucji, możesz wywnioskować inne właściwości danych. Ogólnie rzecz biorąc, można uzyskać lepsze przewidywania z modelu, gdy można zidentyfikować dystrybucję, która najlepiej pasuje do danych.
Pytanie, której funkcji rozkładu prawdopodobieństwa użyć zależy od danych i zmiennych, które są mierzone. Na przykład niektóre rozkłady są przeznaczone do opisywania prawdopodobieństwa wartości dyskretnych; inne są przeznaczone do użytku tylko ze zmiennymi liczbowymi ciągłymi. W przypadku niektórych rozkładów należy również znać z wyprzedzeniem oczekiwaną średnią, stopień swobody itd. Aby uzyskać szczegółowe informacje, zobacz Obsługiwane rozkłady prawdopodobieństwa
How to configure Evaluate Probability Function
Wszystkie opcje zmieniają się w zależności od typu rozkładu prawdopodobieństwa, który chcesz obliczyć. Jeśli zmienisz metodę rozkładu prawdopodobieństwa, inne wybory, które mogły zostać wprowadzone, zostaną zresetowane.
Dlatego należy najpierw wybrać opcję Dystrybucja .
Zestaw danych używany jako dane wejściowe powinien zawierać dane liczbowe. Inne typy danych są ignorowane.
Dla każdej analizy można zastosować pojedynczą metodę rozkładu prawdopodobieństwa. Aby obliczyć inny rozkład prawdopodobieństwa, dodaj oddzielne wystąpienie modułu dla każdej dystrybucji, którą zamierzasz przetestować.
Dodaj moduł Evaluate Probability Function (Ocena funkcji prawdopodobieństwa ) do eksperymentu. Ten moduł można znaleźć w kategorii Funkcje statystyczne w programie Machine Learning Studio (wersja klasyczna).
Połączenie zestaw danych zawierający co najmniej jedną kolumnę liczb.
Użyj opcji Dystrybucja , aby wybrać rodzaj rozkładu prawdopodobieństwa, który chcesz obliczyć. Zobacz Obsługiwane rozkłady prawdopodobieństwa , aby uzyskać listę opcji i ich wymaganych argumentów.
Ustaw wszystkie parametry wymagane przez dystrybucję.
Wybierz jedną z trzech statystyk do utworzenia: funkcję rozkładu skumulowanego (cdf), funkcję odwrotnego rozkładu skumulowanego (InverseCdf) lub funkcję gęstości prawdopodobieństwa (pdf).
Zobacz sekcję Uwagi techniczne , aby zapoznać się z definicjami.
Użyj selektora kolumn, aby wybrać kolumny, dla których ma być obliczany wybrany rozkład prawdopodobieństwa.
Wszystkie wybrane kolumny muszą mieć typ danych liczbowych.
Zakres danych w kolumnie musi być również prawidłowy, biorąc pod uwagę wybraną funkcję prawdopodobieństwa. W przeciwnym razie może wystąpić błąd lub wynik NaN.
W przypadku kolumn rozrzedzona żadne wartości, które odpowiadają zerom tła, nie będą przetwarzane.
Użyj opcji Tryb wyników , aby określić sposób wyświetlania wyników. Wartości kolumn można zastąpić wartościami rozkładu prawdopodobieństwa, dołączyć nowe wartości do zestawu danych lub zwrócić tylko wartości rozkładu prawdopodobieństwa.
Uruchom eksperyment lub kliknij prawym przyciskiem myszy moduł Evaluate Probability Function (Ocena funkcji prawdopodobieństwa ), a następnie kliknij polecenie Uruchom wybrane.
Wyniki
Poniższa tabela zawiera przykład wyników z użyciem opcji Dołączanie w pojedynczej kolumnie temperatury z przykładowego zestawu danych Forest Fires .
| tymczasowe | StandardNormal.Cdf(temp) | StandardNormal.Pdf(temp) | FFisher.cdf(temp) | FFisher.cdf(temp) |
|---|---|---|---|---|
| 8.2 | 1 | 1 | 0.984774 | 0.004349 |
| 18 | 1 | 1 | 0.997896 | 0.000311 |
| 14.6 | 1 | 1 | 0.996352 | 0.000648 |
| 8.3 | 1 | 1 | 0.985201 | 0.004187 |
| 11,4 | 1 | 1 | 0.993147 | 0.001502 |
Nagłówki wygenerowanych kolumn zawierają rozkład prawdopodobieństwa, który został użyty.
Jeśli nie masz pewności, który rozkład prawdopodobieństwa może odpowiadać danym, możesz utworzyć szybki wykres skumulowanego rozkładu i gęstości prawdopodobieństwa dla dowolnej kolumny liczbowej.
- Kliknij prawym przyciskiem myszy dane wyjściowe zestawu danych lub modułu, a następnie wybierz pozycję Visualize (Wizualizuj).
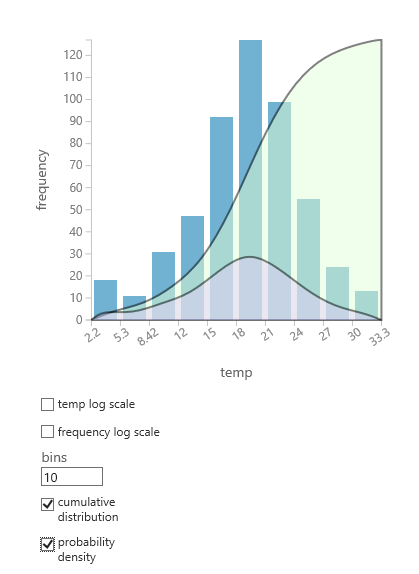
- Wybierz kolumnę zainteresowania, a następnie w okienku Histogram wybierz skumulowany rozkład lub gęstość prawdopodobieństwa.
- Wykres rozkładu, podobnie jak poniżej, jest nakładany na histogram reprezentujący dane.
Obsługiwane rozkłady prawdopodobieństwa
Moduł Evaluate Probability Function (Ocena funkcji prawdopodobieństwa ) obsługuje następujące dystrybucje:
Bernoulliego
Rozkład Bernoulli jest rozkładem wartości binarnych: innymi słowy modeluje oczekiwany rozkład, gdy tylko dwie wartości są możliwe.
Aby obliczyć, wybierz pozycję Bernoulli i ustaw następujące opcje:
- Prawdopodobieństwo sukcesu
Parametr p określa prawdopodobieństwo wygenerowania wartości 1. Wpisz liczbę (float) z zakresu od 0,0 do 1,0, która określa prawdopodobieństwo sukcesu. Wartość domyślna to .5.
Beta
Rozkład beta jest ciągłym, niezmiennym rozkładem.
Aby obliczyć, wybierz pozycję Beta i ustaw następujące opcje:
Kształt
Wpisz wartość, aby zmienić kształt rozkładu.Parametr kształtu jest dowolnym parametrem rozkładu prawdopodobieństwa, który nie definiuje jego lokalizacji ani skali. W związku z tym po wprowadzeniu wartości kształtu parametr zmienia kształt rozkładu zamiast przenosić, rozciągać lub zmniejszać go.
Wartość musi być liczbą (
double). Wartość domyślna to 1.0.Skalowanie
Wpisz liczbę, która ma być używana do skalowania dystrybucji.Stosując wartość skalowania do rozkładu, można ją zmniejszyć lub rozciągnąć.
Wartość domyślna to 1.0. Wartości muszą być liczbami dodatnimi.
Górna granica
Wpisz liczbę (double), która reprezentuje górną granicę rozkładu. Wartość domyślna to 1.0.Dolna granica
Wpisz liczbę (double), która reprezentuje dolną granicę rozkładu. Wartość domyślna to 0,0.
Dwumianowy
Rozkład binomialny jest dyskretnym, niewariancyjnym rozkładem. Rozkład dwumianowy służy do modelowania liczby sukcesów w próbce. Zamiana jest używana podczas próbkowania. W przypadku próbkowania bez zamiany należy użyć rozkładu hipergeometrycznego.
Aby obliczyć, wybierz pozycję Binomial i ustaw następujące opcje:
Prawdopodobieństwo sukcesu
Wpisz liczbę (float) z zakresu od 0,0 do 1,0, która wskazuje prawdopodobieństwo sukcesu. Wartość domyślna to .5.Liczba prób
Określ liczbę prób.Użyj wartości
integer, z minimalną wartością 1. Wartość domyślna to 3.
Cauchy'ego
Rozkład Cauchy jest symetrycznym ciągłym rozkładem prawdopodobieństwa.
Aby obliczyć, wybierz pozycję Cauchy i ustaw następujące opcje:
Lokalizacja
Wpisz liczbę (double), która reprezentuje lokalizacjęelementu 0.Określając wartość parametru Location , można przesunąć rozkład prawdopodobieństwa w górę lub w dół skali liczbowej.
Wartość domyślna to 0,0.
ChiSquare
Rozkład chi-square jest sumą kwadratów k niezależnych, standardowych, normalnych, losowych zmiennych.
Aby obliczyć, wybierz pozycję ChiSquare i ustaw następujące opcje:
- Liczba stopni swobody Wpisz liczbę (
double), aby określić stopień swobody. Wartość domyślna to 1.0.
ChiSquareRightTailed
Ta opcja zapewnia rozkład prostokątny chi kwadratu.
Aby obliczyć, wybierz pozycję ChiSquareRightTailed i ustaw następujące opcje:
- Liczba stopni swobody
Wpisz liczbę (double), aby określić stopień swobody. Wartość domyślna to 1.0.
Wykładniczy
Rozkład wykładniczy jest rozkładem liczb rzeczywistych sparametryzowanych przez jeden parametr nieujemny.
Aby obliczyć, wybierz pozycję Wykładniczo i ustaw następujące opcje:
- Lambda
Wpisz liczbę (double), która ma być używana jako parametr lambda. Wartość domyślna to 1.0.
FFisher
Generuje prawdopodobieństwo statystyki Fisher dla próbki, znanej również jako rozkład F Fisher. Ten rozkład jest dwuuńcowy.
Aby obliczyć, wybierz pozycję FFisher i ustaw następujące opcje:
Stopnie swobody licznika
Wpisz liczbę (double), aby określić stopnie swobody używane w liczniku. Wartość domyślna to 3.0.Stopnie swobody mianownika
Wpisz liczbę (double), aby określić stopień swobody używanej w mianowniku. Wartość domyślna to 6.0.
FFisherRightTailed
Tworzy rozkład fisherów z prawej strony. Rozkład Fisher jest również znany jako rozkład Fisher F, Rozkład Snedecor lub Fisher-Snedecor rozkład. Ta konkretna forma rozkładu jest właściwa.
Aby obliczyć, wybierz pozycję FFisherRightTailed i ustaw następujące opcje:
Stopnie swobody licznika
Wpisz liczbę (double), aby określić stopnie swobody używane w liczniku. Wartość domyślna to 3.0.Stopnie swobody mianownika
Wpisz liczbę (double), aby określić stopień swobody używanej w mianowniku. Wartość domyślna to 6.0.
Gamma
Rozkład gamma jest rodziną ciągłych rozkładów prawdopodobieństwa z dwoma parametrami. Na przykład chi-squared jest specjalnym przypadkiem rozkładu gamma.
Aby obliczyć, wybierz pozycję Gamma i ustaw następujące opcje:
Skalowanie
Wpisz wartość, która ma być używana do skalowania dystrybucji.Stosując wartość skalowania do rozkładu, można ją zmniejszyć lub rozciągnąć.
Wartość domyślna to 1.0. Wartości muszą być liczbami dodatnimi.
Lokalizacja
Wpisz liczbę (double), która reprezentuje lokalizacjęelementu 0.Określając wartość parametru Location , można przesunąć rozkład prawdopodobieństwa w górę lub w dół skali liczbowej.
Wartość domyślna to 0,0.
GeneralizedExtremeValues
Tworzy rozkład opracowany w celu obsługi ekstremalnych wartości. Rozkład uogólnionej wartości skrajnej (GEV) jest w rzeczywistości grupą rozkładów ciągłych prawdopodobieństwa łączących rozkłady Gumbel, Fréchet i Weibull (znane również jako rozkłady skrajnych wartości typu I, II i III).
Aby uzyskać więcej informacji na temat teorii skrajnej wartości, zobacz ten artykuł w Wikipedii: Twierdzenie Fisher-Tippet-Gnedenko.
Aby obliczyć, wybierz pozycję GeneralizedExtremeValues i ustaw następujące opcje:
Kształt
Wpisz wartość, aby zmienić kształt rozkładu.Parametr kształtu jest dowolnym parametrem rozkładu prawdopodobieństwa, który nie definiuje jego lokalizacji ani skali. W związku z tym po wprowadzeniu wartości kształtu parametr zmienia kształt rozkładu zamiast przenosić, rozciągać lub zmniejszać go.
Wartość musi być liczbą (
double). Wartość domyślna to 1.0.Skalowanie
Wpisz wartość, która ma być używana do skalowania dystrybucji.Stosując wartość skalowania do rozkładu, można ją zmniejszyć lub rozciągnąć.
Wartość domyślna to 1.0. Wartości muszą być liczbami dodatnimi.
Lokalizacja
Wpisz liczbę (double), która reprezentuje lokalizacjęelementu 0.Wpisując wartość parametru Location , można przesunąć rozkład prawdopodobieństwa w górę lub w dół skali liczbowej.
Wartość domyślna to 0,0.
Geometryczne
Rozkład geometryczny jest rozkładem dodatnich liczb całkowitych sparametryzowanych przez jedną dodatnią liczbę rzeczywistą.
Aby obliczyć, wybierz pozycję Geometryczne i ustaw następujące opcje:
- Prawdopodobieństwo sukcesu
Wpisz liczbę (float) z zakresu od 0,0 do 1,0, która wskazuje prawdopodobieństwo sukcesu. Wartość domyślna to .5.
Uwaga
Ta implementacja rozkładu geometrycznego nie generuje zer.
GumbelMax
Rozkład Gumbel jest jednym z kilku skrajnych rozkładów wartości. Opcja GumbelMax implementuje rozkład maksymalnej wartości skrajnej typu 1.
Aby obliczyć, wybierz pozycję GumbelMax i ustaw następujące opcje:
Skalowanie
Wpisz wartość, która ma być używana do skalowania dystrybucji.Stosując wartość skalowania do rozkładu, można ją zmniejszyć lub rozciągnąć.
Wartość domyślna to 1.0. Wartości muszą być liczbami dodatnimi.
Lokalizacja
Wpisz liczbę (double), która reprezentuje lokalizacjęelementu 0.Wpisując wartość parametru Location , można przesunąć rozkład prawdopodobieństwa w górę lub w dół skali liczbowej.
Wartość domyślna to 0,0.
GumbelMin
Rozkład Gumbel jest jednym z kilku skrajnych rozkładów wartości. Rozkład Gumbel jest również określany jako rozkład najmniejszych wartości skrajnych (SEV) lub rozkład najmniejszej wartości skrajnej (typu I). Opcja GumbelMin implementuje rozkład minimalnej wartości skrajnej typu 1.
Aby obliczyć, wybierz pozycję GumbelMin i musisz ustawić następujące opcje:
Skalowanie
Wpisz wartość, która ma być używana do skalowania dystrybucji.Stosując wartość skalowania do rozkładu, można ją zmniejszyć lub rozciągnąć.
Wartość domyślna to 1.0. Wartości muszą być liczbami dodatnimi.
Lokalizacja
Wpisz liczbę (double), która reprezentuje lokalizacjęelementu 0.Wpisując wartość parametru Location , można przesunąć rozkład prawdopodobieństwa w górę lub w dół skali liczbowej.
Wartość domyślna to 0,0.
Hipergeometryczna
Rozkład hipergeometryczny jest dyskretnym rozkładem prawdopodobieństwa, który opisuje liczbę sukcesów w sekwencji n pobieranych z populacji skończonej bez zamiany, tak jak rozkład dwumianowy opisuje liczbę sukcesów dla losowań z zastąpieniem.
Aby obliczyć, wybierz pozycję Hypergeometric i ustaw następujące opcje:
Liczba próbek
Wpisz liczbę całkowitą, która wskazuje liczbę próbek do użycia. Wartość domyślna to 9.Liczba sukcesów
Wpisz liczbę całkowitą, która definiuje wartość powodzenia. Wartość domyślna to 24.Rozmiar populacji
Określ rozmiar populacji, który ma być używany podczas szacowania rozkładu hipergeometrycznego.
Laplace
Rozkład Laplace jest rozkładem liczb rzeczywistych, sparametryzowanym przez średnią i przez parametr skalowania.
Aby obliczyć, wybierz pozycję Rozkład laplace i ustaw następujące opcje:
Skalowanie
Wpisz wartość, która ma być używana do skalowania dystrybucji.Stosując wartość skalowania do rozkładu, można ją zmniejszyć lub rozciągnąć.
Wartość domyślna to 1.0. Wartości muszą być liczbami dodatnimi.
Lokalizacja
Wpisz liczbę (double), która reprezentuje lokalizacjęelementu 0.Wpisując wartość parametru Location , można przesunąć rozkład prawdopodobieństwa w górę lub w dół skali liczbowej.
Wartość domyślna to 0,0.
Logistyczne
Rozkład logistyczny jest podobny do rozkładu normalnego, ale nie ma limitu po lewej stronie rozkładu. Dystrybucja logistyczna jest używana w modelach regresji logistycznej i sieci neuronowej oraz modelowaniu danych nauk życiowych.
Aby obliczyć, wybierz pozycję Logistyka i ustaw następujące opcje:
Skalowanie
Wpisz wartość, która ma być używana do skalowania dystrybucji.Stosując wartość skalowania do rozkładu, można ją zmniejszyć lub rozciągnąć.
Wartość domyślna to 1.0. Wartości muszą być liczbami dodatnimi.
Oznacza
Wpisz liczbę (double),która wskazuje szacowaną średnią wartość rozkładu. Wartość domyślna to 0,0.
Lognormal (Nieprawidłowości w dzienniku
Rozkład lognormalny jest ciągłym, niezmiennym rozkładem.
Aby obliczyć, wybierz pozycję Lognormal i ustaw następujące opcje:
Oznacza
Wpisz liczbę (double), która wskazuje szacowaną średnią wartość rozkładu. Wartość domyślna to 0,0.Odchylenie standardowe
Wpisz liczbę dodatnią (double), która wskazuje szacowane odchylenie standardowe rozkładu. Wartość domyślna to 1.0.
Ujemnebinomie
Ujemny rozkład binomialny jest rozkładem liczb naturalnych z dwoma parametrami (r, p). W specjalnym przypadku, który r jest liczbą całkowitą, można zinterpretować rozkład jako liczbę ogonów przed rth head, gdy prawdopodobieństwo głowy jest p.
Aby obliczyć, wybierz pozycję NegativeBinomial i ustaw następujące opcje:
Prawdopodobieństwo sukcesu
Wpisz liczbę (float) z zakresu od 0,0 do 1,0, która wskazuje prawdopodobieństwo sukcesu. Wartość domyślna to .5.Liczba sukcesów
Wpisz liczbę całkowitą określającą wartość powodzenia. Wartość domyślna to 24.
Normalne
Rozkład normalny jest również znany jako rozkład gaussański.
Aby obliczyć, wybierz pozycję Normalny i ustaw następujące opcje:
Oznacza
Wpisz liczbę (double), która wskazuje szacowaną średnią wartość rozkładu. Wartość domyślna to 0,0.Odchylenie standardowe
Wpisz liczbę dodatnią (double), która wskazuje szacowane odchylenie standardowe rozkładu. Wartość domyślna to 1.0.
Pareto
Rozkład Pareto jest rozkładem prawdopodobieństwa prawa władzy, który pokrywa się z społecznym, naukowym, geofizycznym, aktuarialnym i wieloma innymi rodzajami obserwowanych zjawisk.
Aby obliczyć, wybierz pozycję Pareto i ustaw następujące opcje:
Kształt
Wpisz wartość (opcjonalnie), aby zmienić kształt rozkładu.Parametr kształtu jest dowolnym parametrem rozkładu prawdopodobieństwa, który nie definiuje jego lokalizacji ani skali. W związku z tym po wprowadzeniu wartości kształtu parametr zmienia kształt rozkładu zamiast przenosić, rozciągać lub zmniejszać go.
Wartość musi być liczbą (
double). Wartość domyślna to 1.0.Skalowanie
Wpisz wartość (opcjonalnie), aby zmienić skalę rozkładu. Stosując wartość skalowania do rozkładu, można ją zmniejszyć lub rozciągnąć.Wartość musi być liczbą (
double). Wartość domyślna to 1.0.
Poisson
W tej implementacji metoda Knuth jest używana do generowania rozproszonych zmiennych losowych Poissona. Aby uzyskać więcej informacji na temat rozkładu Poissona, zobacz Regresja Poissona.
Aby obliczyć, wybierz pozycję Poisson i ustaw następujące opcje:
- Oznacza
Wpisz liczbę (double), która wskazuje szacowaną średnią wartość rozkładu. Wartość domyślna to 0,0.
Rayleigh
Rozkład Rayleigh jest ciągłym rozkładem prawdopodobieństwa. Jako przykład tego, jak się pojawi, prędkość wiatru będzie miała rozkład Rayleigh, jeśli składniki dwuwymiarowego wektora prędkości wiatru są nieskorelowane i zwykle rozłożone z równą wariancją.
Aby obliczyć, wybierz pozycję Rayleigh i ustaw następujące opcje:
- Dolna granica
Wpisz liczbę (double), która reprezentuje dolną granicę rozkładu. Wartość domyślna to 0,0.
StandardNormal
Ta opcja zapewnia standardowy rozkład normalny, bez innych parametrów.
Aby obliczyć, wybierz pozycję StandardNormal i wybierz kolumny.
TStudent
Ta opcja implementuje niezmienny rozkład t-studenta.
Aby obliczyć, wybierz pozycję TStudent i ustaw następujące opcje:
- Liczba stopni swobody
Wpisz liczbę (double), aby określić stopień swobody. Wartość domyślna to 1.0.
TStudentRightTailed
Implementuje niezmienny rozkład t-studenta przy użyciu jednego prawego ogona.
Aby obliczyć, wybierz pozycję TStudentRightTailed i ustaw następujące opcje:
- Liczba stopni swobody
Wpisz liczbę (double), aby określić stopień swobody. Wartość domyślna to 1.0.
TStudentTwoTailed
Implementuje rozkład t-studenta z dwoma ogonami.
Aby obliczyć, wybierz pozycję TStudentTwoTailed i ustaw następujące opcje:
- Liczba stopni swobody
Wpisz liczbę (double), aby określić stopień swobody. Wartość domyślna to 1.0.
Jednolite
Rozkład jednolity jest również znany jako rozkład prostokątny.
Aby obliczyć, wybierz pozycję Jednolite i ustaw następujące opcje:
Dolna granica
Wpisz liczbę (double), która reprezentuje niższy limit rozkładu. Wartość domyślna to 0,0.Górna granica
Wpisz liczbę (double), która reprezentuje górny limit rozkładu. Wartość domyślna to 1.0.
Rozkład.weibull
Dystrybucja Weibulla jest powszechnie stosowana w inżynierii niezawodności. Można użyć jego parametru Shape do modelowania wielu innych dystrybucji.
Aby obliczyć, wybierz pozycję Weibull i ustaw następujące opcje:
Kształt
Wpisz wartość (opcjonalnie), aby zmienić kształt rozkładu.Parametr kształtu jest dowolnym parametrem rozkładu prawdopodobieństwa, który nie definiuje jego lokalizacji ani skali. W związku z tym po wprowadzeniu wartości kształtu parametr zmienia kształt rozkładu zamiast przenosić, rozciągać lub zmniejszać go.
Wartość musi być liczbą (
double). Wartość domyślna to 1.0.Skalowanie
Wpisz wartość (opcjonalnie), aby zmienić skalę rozkładu. Stosując wartość skalowania do rozkładu, można ją zmniejszyć lub rozciągnąć.Wartość musi być liczbą (
double). Wartość domyślna to 1.0.
Uwagi techniczne
Ta sekcja zawiera szczegóły implementacji, porady i odpowiedzi na często zadawane pytania.
Szczegóły implementacji
Ten moduł obsługuje wszystkie dystrybucje, które znajdują się w bibliotece open source MATH.NET Numeryczne. Aby uzyskać więcej informacji, zobacz dokumentację biblioteki Math.Net.Numerics.Distribution .
Rozkłady ogonowe i dwuuwrotne są wyświetlane jako oddzielne rozkłady, a nie jako sparametryzowane wersje rozkładów podstawowych. Bieżące zachowanie polega na zachowaniu zgodności z Excel.
Definicje
Ten moduł obsługuje obliczanie dowolnej z tych wartości dla określonej dystrybucji:
cdf lub funkcja rozkładu skumulowanego
Zwraca prawdopodobieństwo zdarzenia złożonego zdefiniowanego jako suma currences, gdy zmienna losowa przyjmuje wartość mniejszą niż określona wartość x.
Innymi słowy, odpowiada na pytanie: "Jak często próbki są mniejsze niż lub równe tej wartości?"
Tej funkcji można używać zarówno ze zmiennymi ciągłymi, jak i dyskretnymi liczbowymi.
InverseCdf lub odwrotna funkcja rozkładu skumulowanego
Zwraca wartość skojarzona z określoną skumulowaną wartością prawdopodobieństwa (cdf).
Innymi słowy, odpowiada na pytanie: "Jaka jest wartość x, przy której funkcja cdf zwraca skumulowane prawdopodobieństwo y?"
pdf lub funkcja gęstości prawdopodobieństwa
Opisuje względne prawdopodobieństwo, że zmienna losowa ma być określoną wartością.
Innymi słowy, odpowiada na pytanie: "Jak często próbki są dokładnie takie?"
Oczekiwane dane wejściowe
| Nazwa | Typ | Opis |
|---|---|---|
| Zestaw danych | Tabela danych | Wejściowy zestaw danych |
Parametry modułu
| Nazwa | Zakres | Typ | Domyślny | Opis |
|---|---|---|---|---|
| Dystrybucja | Dowolne | ProbabilityDistribution | StandardNormal | Wybierz rodzaj rozkładu prawdopodobieństwa do wygenerowania. |
| Metoda | Dowolne | ProbabilityDistributionMethod | Cdf | Wybierz metodę do użycia podczas obliczania wybranego rozkładu prawdopodobieństwa. Opcje to funkcja rozkładu skumulowanego (cdf), funkcja odwrotnego rozkładu skumulowanego (InverseCdf) oraz funkcja gęstości prawdopodobieństwa lub funkcja masy (pdf). |
| Ujemna metoda rozkładu binomialnego | Dowolne | ProbabilityDistributionMethodForNegativeBinomial | Cdf | W przypadku wybrania ujemnego rozkładu binomialnego określ metodę używaną do oceny rozkładu. |
| Prawdopodobieństwo sukcesu | [0.0;1.0] | Float | 0,5 | Wpisz wartość, która ma być używana jako prawdopodobieństwo sukcesu. |
| Kształt | Dowolne | Float | 1.0 | Wpisz wartość, która modyfikuje kształt rozkładu. |
| Skalowanie | >=0.0 | Float | 1.0 | Wpisz wartość, która zmienia skalę rozkładu w celu rozwinięcia lub zmniejszenia rozmiaru. |
| Liczba prób | >=1 | Liczba całkowita | 3 | Określ liczbę prób. |
| Dolna granica | Dowolne | Float | 0,0 | Wpisz liczbę, która ma być używana jako niższy limit rozkładu |
| Górna granica | Dowolne | Float | 1.0 | Wpisz liczbę, która ma być używana jako górny limit rozkładu |
| Lokalizacja | Dowolne | Float | 0,0 | Wpisz lokalizację elementu zero w dystrybucji. |
| Liczba stopni swobody | Dowolne | Float | 1.0 | Określ liczbę stopni swobody. |
| Stopnie swobody licznika | Dowolne | Float | 3.0 | Określ liczbę stopni swobody w liczniku. |
| Stopnie swobody mianownika | Dowolne | Float | 6.0 | Określ liczbę stopni swobody w mianowniku. |
| Lambda | >=0.0 | Float | 1.0 | Określ wartość parametru lambda. |
| Liczba próbek | Dowolne | Liczba całkowita | 9 | Określ liczbę próbek. |
| Liczba sukcesów | Dowolne | Liczba całkowita | 24 | Wpisz wartość, która ma być używana jako liczba powodzenia. |
| Rozmiar populacji | Dowolne | Liczba całkowita | 52 | Określ rozmiar populacji. |
| Średnia | Dowolne | Float | 0,0 | Wpisz szacowaną wartość średniej. |
| Odchylenie standardowe | >=0.0 | Float | 1.0 | Wpisz szacowane odchylenie standardowe. |
| Zestaw kolumn | Dowolne | KolumnaWybieranie | Wybierz kolumny, dla których ma być obliczany rozkład prawdopodobieństwa. | |
| Tryb wyników | Dowolne | Wyprowadźdo | ResultOnly | Określ sposób zapisywania wyników w wyjściowym zestawie danych. Opcje są przeznaczone do dołączania nowych kolumn, zastępowania istniejących kolumn lub danych wyjściowych tylko wyników. |
Dane wyjściowe
| Nazwa | Typ | Opis |
|---|---|---|
| Zestaw danych wyników | Tabela danych | Wyjściowy zestaw danych |
Wyjątek
Aby uzyskać pełną listę komunikatów o błędach, zobacz Kody błędów modułu.
| Wyjątek | Opis |
|---|---|
| Błąd 0017 | Wyjątek występuje, jeśli co najmniej jedna określona kolumna ma typ, który nie jest obsługiwany przez bieżący moduł. |
Aby uzyskać listę błędów specyficznych dla modułów programu Studio (klasycznych), zobacz Machine Learning Kody błędów.
Aby uzyskać listę wyjątków interfejsu API, zobacz Machine Learning kody błędów interfejsu API REST.