Del via

Utvikle, evaluere og få en prognosemodell for butikksalg

  • Artikkel

Denne opplæringen presenterer et ende-til-ende-eksempel på en Synapse Data Science-arbeidsflyt i Microsoft Fabric. Scenarioet bygger en prognosemodell som bruker historiske salgsdata til å forutsi salg av produktkategorier i en superlager.

Prognoser er et viktig aktivum i salg. Den kombinerer historiske data og prediktive metoder for å gi innsikt i fremtidige trender. Prognoser kan analysere tidligere salg for å identifisere mønstre og lære av forbrukeratferd for å optimalisere lager-, produksjons- og markedsføringsstrategier. Denne proaktive tilnærmingen forbedrer tilpasningsevne, respons og generell ytelse for bedrifter i en dynamisk markedsplass.

Denne opplæringen dekker disse trinnene:

  • Laste inn dataene
  • Bruk utforskende dataanalyse til å forstå og behandle dataene
  • Lær opp en maskinlæringsmodell med en åpen kildekode-programvarepakke, og spor eksperimenter med MLflow og fabric autologging-funksjonen
  • Lagre den endelige maskinlæringsmodellen, og lag prognoser
  • Vis modellytelsen med Power BI-visualiseringer

Forutsetninger

Følg med i en notatblokk

Du kan velge ett av disse alternativene for å følge med i en notatblokk:

  • Åpne og kjøre den innebygde notatblokken i Synapse Data Science-opplevelsen
  • Last opp notatblokken fra GitHub til Synapse Data Science-opplevelsen

Åpne den innebygde notatblokken

Eksemplet Salgsprognoser notatblokk følger med denne opplæringen.

  1. Hvis du vil åpne eksempelnotatblokken for denne opplæringen, følger du instruksjonene i Klargjør systemet for.

  2. Pass på å feste et lakehouse til notatblokken før du begynner å kjøre kode.

Importere notatblokken fra GitHub

AIsample – Superstore Forecast.ipynb notatblokk følger med denne opplæringen.

Trinn 1: Laste inn dataene

Datasettet inneholder 9995 forekomster av salg av ulike produkter. Den inneholder også 21 attributter. Denne tabellen er fra Superstore.xlsx filen som brukes i denne notatblokken:

Rad-ID Ordre-ID Ordredato Forsendelsesdato Forsendelsesmodus Kunde-ID Kundenavn Innslag Land By Tilstand Postnummer Region Produkt-ID Kategori Sub-Category Produktnavn Salg Kvantitet Rabatt Profitt
4 USA-2015-108966 2015-10-11 2015-10-18 Standardklasse SO-20335 Sean O'Donnell Forbruker USA Fort Lauderdale Florida 33311 Sør FUR-TA-10000577 Møbel Tabeller Bretford CR4500 Series Slim Rectangular Table 957.5775 5 0.45 -383.0310
11 CA-2014-115812 2014-06-09 2014-06-09 Standardklasse Standardklasse Brosina Hoffman Forbruker USA Los Angeles California 90032 Vest FUR-TA-10001539 Møbel Tabeller Chromcraft Rektangulære konferansetabeller 1706.184 9 0.2 85.3092
31 USA-2015-150630 2015-09-17 2015-09-21 Standardklasse TB-21520 Tracy Blumstein Forbruker USA Philadelphia Pennsylvania 19140 Øst OFF-EN-10001509 Office Supplies Konvolutter Poly String Tie-konvolutter 3.264 2 0.2 1.1016

Definer disse parameterne, slik at du kan bruke denne notatblokken med forskjellige datasett:

IS_CUSTOM_DATA = False  # If TRUE, the dataset has to be uploaded manually

IS_SAMPLE = False  # If TRUE, use only rows of data for training; otherwise, use all data
SAMPLE_ROWS = 5000  # If IS_SAMPLE is True, use only this number of rows for training

DATA_ROOT = "/lakehouse/default"
DATA_FOLDER = "Files/salesforecast"  # Folder with data files
DATA_FILE = "Superstore.xlsx"  # Data file name

EXPERIMENT_NAME = "aisample-superstore-forecast"  # MLflow experiment name

Last ned datasettet og last opp til lakehouse

Denne koden laster ned en offentlig tilgjengelig versjon av datasettet, og lagrer den deretter i et Fabric Lakehouse:

Viktig

Pass på å legge til et lakehouse- i notatblokken før du kjører den. Ellers får du en feilmelding.

import os, requests
if not IS_CUSTOM_DATA:
    # Download data files into the lakehouse if they're not already there
    remote_url = "https://synapseaisolutionsa.blob.core.windows.net/public/Forecast_Superstore_Sales"
    file_list = ["Superstore.xlsx"]
    download_path = "/lakehouse/default/Files/salesforecast/raw"

    if not os.path.exists("/lakehouse/default"):
        raise FileNotFoundError(
            "Default lakehouse not found, please add a lakehouse and restart the session."
        )
    os.makedirs(download_path, exist_ok=True)
    for fname in file_list:
        if not os.path.exists(f"{download_path}/{fname}"):
            r = requests.get(f"{remote_url}/{fname}", timeout=30)
            with open(f"{download_path}/{fname}", "wb") as f:
                f.write(r.content)
    print("Downloaded demo data files into lakehouse.")

Konfigurere sporing av MLflow-eksperimenter

Microsoft Fabric registrerer automatisk verdiene for inndataparametere og utdatadata for en maskinlæringsmodell mens du lærer opp den. Dette utvider egenskapene for automatisk tillogging av MLflow. Informasjonen logges deretter på arbeidsområdet, der du kan få tilgang til og visualisere den med MLflow-API-ene eller det tilsvarende eksperimentet i arbeidsområdet. Hvis du vil ha mer informasjon om autologging, kan du se Autologging i Microsoft Fabric.

Hvis du vil deaktivere Automatisk tillogging av Microsoft Fabric i en notatblokkøkt, ringer du mlflow.autolog() og angir disable=True:

# Set up MLflow for experiment tracking
import mlflow

mlflow.set_experiment(EXPERIMENT_NAME)
mlflow.autolog(disable=True)  # Turn off MLflow autologging

Les rådata fra lakehouse

Les rådata fra Files-delen av lakehouse. Legg til flere kolonner for ulike datodeler. Den samme informasjonen brukes til å opprette en partisjonert deltatabell. Siden rådataene lagres som en Excel-fil, må du bruke pandaer til å lese dem:

import pandas as pd
df = pd.read_excel("/lakehouse/default/Files/salesforecast/raw/Superstore.xlsx")

Trinn 2: Utfør utforskende dataanalyse

Importere biblioteker

Før en analyse importerer du de nødvendige bibliotekene:

# Importing required libraries
import warnings
import itertools
import numpy as np
import matplotlib.pyplot as plt
warnings.filterwarnings("ignore")
plt.style.use('fivethirtyeight')
import pandas as pd
import statsmodels.api as sm
import matplotlib
matplotlib.rcParams['axes.labelsize'] = 14
matplotlib.rcParams['xtick.labelsize'] = 12
matplotlib.rcParams['ytick.labelsize'] = 12
matplotlib.rcParams['text.color'] = 'k'
from sklearn.metrics import mean_squared_error,mean_absolute_percentage_error

Vise rådataene

Se gjennom et delsett av dataene manuelt for bedre å forstå selve datasettet, og bruk display-funksjonen til å skrive ut DataFrame. I tillegg kan Chart visninger enkelt visualisere delsett av datasettet.

display(df)

Denne notatblokken fokuserer primært på prognoser for Furniture kategorisalg. Dette øker hastigheten på beregningen, og bidrar til å vise ytelsen til modellen. Denne notatblokken bruker imidlertid tilpasningsdyktige teknikker. Du kan utvide disse teknikkene for å forutsi salg av andre produktkategorier.

# Select "Furniture" as the product category
furniture = df.loc[df['Category'] == 'Furniture']
print(furniture['Order Date'].min(), furniture['Order Date'].max())

Forhåndsbearbeide dataene

Virkelige forretningsscenarioer må ofte forutsi salg i tre forskjellige kategorier:

  • En bestemt produktkategori
  • En bestemt kundekategori
  • En bestemt kombinasjon av produktkategori og kundekategori

Slipp først unødvendige kolonner for å forhåndsbearbeide dataene. Noen av kolonnene (Row ID, Order ID,Customer IDog Customer Name) er unødvendige fordi de ikke har noen innvirkning. Vi ønsker å forutsi det totale salget, på tvers av delstat og område, for en bestemt produktkategori (Furniture), slik at vi kan slippe kolonnene State, Region, Country, Cityog Postal Code. Hvis du vil forutsi salg for en bestemt plassering eller kategori, må du kanskje justere forhåndsbearbeidingstrinnet tilsvarende.

# Data preprocessing
cols = ['Row ID', 'Order ID', 'Ship Date', 'Ship Mode', 'Customer ID', 'Customer Name', 
'Segment', 'Country', 'City', 'State', 'Postal Code', 'Region', 'Product ID', 'Category', 
'Sub-Category', 'Product Name', 'Quantity', 'Discount', 'Profit']
# Drop unnecessary columns
furniture.drop(cols, axis=1, inplace=True)
furniture = furniture.sort_values('Order Date')
furniture.isnull().sum()

Datasettet er strukturert daglig. Vi må bruke kolonnen på nytt Order Date, fordi vi ønsker å utvikle en modell for å forutsi salget på månedlig basis.

Først grupperer du kategorien Furniture etter Order Date. Deretter beregner du summen av den Sales kolonnen for hver gruppe, for å bestemme det totale salget for hver unike Order Date verdi. Send Sales-kolonnen på nytt med MS frekvens, for å aggregere dataene etter måned. Til slutt beregner du gjennomsnittssalgsverdien for hver måned.

# Data preparation
furniture = furniture.groupby('Order Date')['Sales'].sum().reset_index()
furniture = furniture.set_index('Order Date')
furniture.index
y = furniture['Sales'].resample('MS').mean()
y = y.reset_index()
y['Order Date'] = pd.to_datetime(y['Order Date'])
y['Order Date'] = [i+pd.DateOffset(months=67) for i in y['Order Date']]
y = y.set_index(['Order Date'])
maximim_date = y.reset_index()['Order Date'].max()

Demonstrere virkningen av Order Date på Sales for kategorien Furniture:

# Impact of order date on the sales
y.plot(figsize=(12, 3))
plt.show()

Før en statistisk analyse må du importere statsmodels Python-modulen. Det gir klasser og funksjoner for estimering av mange statistiske modeller. Det gir også klasser og funksjoner for å gjennomføre statistiske tester og statistisk datautforskning.

import statsmodels.api as sm

Utfør statistisk analyse

En tidsserie sporer disse dataelementene med angitte intervaller for å bestemme variasjonen av disse elementene i tidsseriemønsteret:

  • nivå: Den grunnleggende komponenten som representerer gjennomsnittsverdien for en bestemt tidsperiode

  • Trend: Beskriver om tidsserien minker, forblir konstant eller øker over tid

  • Sesongavhengighet: Beskriver det periodiske signalet i tidsserien, og ser etter sykliske forekomster som påvirker de økende eller synkende tidsseriemønstrene

  • Støy/Rest: Refererer til tilfeldige svingninger og variasjoner i tidsseriedataene som modellen ikke kan forklare.

I denne koden observerer du disse elementene for datasettet etter forhåndsbearbeidingen:

# Decompose the time series into its components by using statsmodels
result = sm.tsa.seasonal_decompose(y, model='additive')

# Labels and corresponding data for plotting
components = [('Seasonality', result.seasonal),
              ('Trend', result.trend),
              ('Residual', result.resid),
              ('Observed Data', y)]

# Create subplots in a grid
fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(12, 7))
plt.subplots_adjust(hspace=0.8)  # Adjust vertical space
axes = axes.ravel()

# Plot the components
for ax, (label, data) in zip(axes, components):
    ax.plot(data, label=label, color='blue' if label != 'Observed Data' else 'purple')
    ax.set_xlabel('Time')
    ax.set_ylabel(label)
    ax.set_xlabel('Time', fontsize=10)
    ax.set_ylabel(label, fontsize=10)
    ax.legend(fontsize=10)

plt.show()

Plottene beskriver sesongavhengighet, trender og støy i prognosedataene. Du kan fange opp de underliggende mønstrene og utvikle modeller som gir nøyaktige prognoser som er motstandsdyktige mot tilfeldige svingninger.

Trinn 3: Lære opp og spore modellen

Nå som du har tilgjengelige data, definerer du prognosemodellen. I denne notatblokken bruker du prognosemodellen kalt sesongbasert autoregressivt integrert glidende gjennomsnitt med eksogene faktorer (SARIMAX). SARIMAX kombinerer autoregressive (AR) og glidende gjennomsnittskomponenter (MA), sesongavhengig differens og eksterne prediktorer for å lage nøyaktige og fleksible prognoser for tidsseriedata.

Du bruker også MLflow og Fabric autologging til å spore eksperimentene. Her laster du deltabordet fra lakehouse. Du kan bruke andre delta bord som anser lakehouse som kilden.

# Import required libraries for model evaluation
from sklearn.metrics import mean_squared_error, mean_absolute_percentage_error

Justere hyperparametere

SARIMAX tar hensyn til parameterne som er involvert i vanlig autoregressiv integrert glidende gjennomsnittsmodus (ARIMA) (p, d, q), og legger til sesongparameterne (P, D, Q, s). Disse SARIMAX-modellargumentene kalles rekkefølge (p, d, q) og sesongrekkefølge ( henholdsvisP, D, Q, s). Derfor, for å lære opp modellen, må vi først justere syv parametere.

Ordreparameterne:

  • p: Rekkefølgen på AR-komponenten, som representerer antall tidligere observasjoner i tidsserien som brukes til å forutsi gjeldende verdi.

    Vanligvis bør denne parameteren være et ikke-negativt heltall. Vanlige verdier er i området 0 til 3, selv om høyere verdier er mulig, avhengig av de spesifikke dataegenskapene. En høyere p verdi angir et lengre minne om tidligere verdier i modellen.

  • d: Den forskjellige rekkefølgen, som representerer antall ganger tidsserien må være differanse, for å oppnå stasjonsbakgrunn.

    Denne parameteren må være et heltall som ikke er negativt. Vanlige verdier er i området 0 til 2. En d verdi for 0 betyr at tidsserien allerede er stasjonær. Høyere verdier angir antall forskjellige operasjoner som kreves for å gjøre det stasjonært.

  • q: Rekkefølgen på MA-komponenten, som representerer antall tidligere termer for hvitstøyfeil som brukes til å forutsi gjeldende verdi.

    Denne parameteren må være et heltall som ikke er negativt. Vanlige verdier er i området 0 til 3, men høyere verdier kan være nødvendig for bestemte tidsserier. En høyere q verdi indikerer en sterkere avhengighet av tidligere feilvilkår for å lage prognoser.

Sesongrekkefølgeparameterne:

  • P: Den sesongavhengige rekkefølgen til AR-komponenten, lik p, men for sesongdelen
  • D: Sesongrekkefølgen av differencing, lik d men for sesongdelen
  • Q: Den sesongavhengige rekkefølgen til MA-komponenten, lik q, men for sesongdelen
  • s: Antall tidstrinn per sesongsyklus (for eksempel 12 for månedlige data med årlig sesongavhengighet)
# Hyperparameter tuning
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
print('Examples of parameter combinations for Seasonal ARIMA...')
print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[1]))
print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[2]))
print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[3]))
print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[4]))

SARIMAX har andre parametere:

  • enforce_stationarity: Om modellen skal håndheve stasjonsbakgrunn på tidsseriedataene, før du tilpasser SARIMAX-modellen.

    Hvis enforce_stationarity er satt til True (standard), angir den at SARIMAX-modellen skal fremtvinge skrivepapir på tidsseriedataene. SARIMAX-modellen bruker deretter automatisk forskjellige data, for å gjøre den stasjonær, som angitt av d og D ordrer, før du tilpasser modellen. Dette er en vanlig praksis fordi mange tidsseriemodeller, inkludert SARIMAX, antar at dataene står stille.

    For en ikke-stasjonær tidsserie (for eksempel viser den trender eller sesongavhengighet), er det god praksis å sette enforce_stationarity til True, og la SARIMAX-modellen håndtere differensen for å oppnå skrivepapir. For en stasjonær tidsserie (for eksempel én uten trender eller sesongavhengighet), kan du angi enforce_stationarity til False for å unngå unødvendig forskjellighet.

  • enforce_invertibility: Kontrollerer om modellen skal håndheve inverterbarhet på de estimerte parameterne under optimaliseringsprosessen.

    Hvis enforce_invertibility er satt til True (standard), angir den at SARIMAX-modellen skal fremtvinge inverterbarhet på de estimerte parameterne. Invertibility ensures that the model is well defined, and that the estimated AR and MA coefficients land within the range of stationarity.

    Invertibility enforcement bidrar til å sikre at SARIMAX-modellen overholder de teoretiske kravene for en stabil tidsseriemodell. Det bidrar også til å forhindre problemer med modellestimering og stabilitet.

Standardverdien er en AR(1) modell. Dette refererer til (1, 0, 0). Det er imidlertid vanlig praksis å prøve forskjellige kombinasjoner av ordreparametere og sesongrekkefølgeparametere, og evaluere modellytelsen for et datasett. De riktige verdiene kan variere fra én serie til en annen.

Fastsettelse av de optimale verdiene innebærer ofte analyse av autokorrelasjonsfunksjonen (ACF) og delvis autokorrelasjonsfunksjon (PACF) for tidsseriedataene. Det innebærer også ofte bruk av kriterier for modellvalg – for eksempel Akaike-informasjonskriteriet (AIC) eller det bayesiske informasjonskriteriet (BIC).

Justere hyperparameterne:

# Tune the hyperparameters to determine the best model
for param in pdq:
    for param_seasonal in seasonal_pdq:
        try:
            mod = sm.tsa.statespace.SARIMAX(y,
                                            order=param,
                                            seasonal_order=param_seasonal,
                                            enforce_stationarity=False,
                                            enforce_invertibility=False)
            results = mod.fit(disp=False)
            print('ARIMA{}x{}12 - AIC:{}'.format(param, param_seasonal, results.aic))
        except:
            continue

Etter evaluering av de foregående resultatene kan du bestemme verdiene for både ordreparameterne og parameterne for sesongrekkefølge. Valget er order=(0, 1, 1) og seasonal_order=(0, 1, 1, 12), som tilbyr den laveste AIC (for eksempel 279,58). Bruk disse verdiene til å lære opp modellen.

Kalibrer modellen

# Model training 
mod = sm.tsa.statespace.SARIMAX(y,
                                order=(0, 1, 1),
                                seasonal_order=(0, 1, 1, 12),
                                enforce_stationarity=False,
                                enforce_invertibility=False)
results = mod.fit(disp=False)
print(results.summary().tables[1])

Denne koden visualiserer en prognose for tidsserier for salgsdata for møbler. De plottede resultatene viser både de observerte dataene og prognosen for ett trinn fremover, med et skyggelagt område for konfidensintervall.

# Plot the forecasting results
pred = results.get_prediction(start=maximim_date, end=maximim_date+pd.DateOffset(months=6), dynamic=False) # Forecast for the next 6 months (months=6)
pred_ci = pred.conf_int() # Extract the confidence intervals for the predictions
ax = y['2019':].plot(label='observed')
pred.predicted_mean.plot(ax=ax, label='One-step ahead forecast', alpha=.7, figsize=(12, 7))
ax.fill_between(pred_ci.index,
                pred_ci.iloc[:, 0],
                pred_ci.iloc[:, 1], color='k', alpha=.2)
ax.set_xlabel('Date')
ax.set_ylabel('Furniture Sales')
plt.legend()
plt.show()

# Validate the forecasted result
predictions = results.get_prediction(start=maximim_date-pd.DateOffset(months=6-1), dynamic=False)
# Forecast on the unseen future data
predictions_future = results.get_prediction(start=maximim_date+ pd.DateOffset(months=1),end=maximim_date+ pd.DateOffset(months=6),dynamic=False)

Bruk predictions til å vurdere modellens ytelse, ved å kontrastere den med de faktiske verdiene. Den predictions_future verdien angir fremtidig prognoser.

# Log the model and parameters
model_name = f"{EXPERIMENT_NAME}-Sarimax"
with mlflow.start_run(run_name="Sarimax") as run:
    mlflow.statsmodels.log_model(results,model_name,registered_model_name=model_name)
    mlflow.log_params({"order":(0,1,1),"seasonal_order":(0, 1, 1, 12),'enforce_stationarity':False,'enforce_invertibility':False})
    model_uri = f"runs:/{run.info.run_id}/{model_name}"
    print("Model saved in run %s" % run.info.run_id)
    print(f"Model URI: {model_uri}")
mlflow.end_run()

# Load the saved model
loaded_model = mlflow.statsmodels.load_model(model_uri)

Trinn 4: Score modellen og lagre prognoser

Integrer de faktiske verdiene med prognoseverdiene for å opprette en Power BI-rapport. Lagre disse resultatene i et bord i lakehouse.

# Data preparation for Power BI visualization
Future = pd.DataFrame(predictions_future.predicted_mean).reset_index()
Future.columns = ['Date','Forecasted_Sales']
Future['Actual_Sales'] = np.NAN
Actual = pd.DataFrame(predictions.predicted_mean).reset_index()
Actual.columns = ['Date','Forecasted_Sales']
y_truth = y['2023-02-01':]
Actual['Actual_Sales'] = y_truth.values
final_data = pd.concat([Actual,Future])
# Calculate the mean absolute percentage error (MAPE) between 'Actual_Sales' and 'Forecasted_Sales' 
final_data['MAPE'] = mean_absolute_percentage_error(Actual['Actual_Sales'], Actual['Forecasted_Sales']) * 100
final_data['Category'] = "Furniture"
final_data[final_data['Actual_Sales'].isnull()]

input_df = y.reset_index()
input_df.rename(columns = {'Order Date':'Date','Sales':'Actual_Sales'}, inplace=True)
input_df['Category'] = 'Furniture'
input_df['MAPE'] = np.NAN
input_df['Forecasted_Sales'] = np.NAN

# Write back the results into the lakehouse
final_data_2 = pd.concat([input_df,final_data[final_data['Actual_Sales'].isnull()]])
table_name = "Demand_Forecast_New_1"
spark.createDataFrame(final_data_2).write.mode("overwrite").format("delta").save(f"Tables/{table_name}")
print(f"Spark DataFrame saved to delta table: {table_name}")

Trinn 5: Visualiser i Power BI

Power BI-rapporten viser en gjennomsnittlig absolutt prosentfeil (MAPE) på 16,58. MAPE-måleverdien definerer nøyaktigheten til en prognosemetode. Det representerer nøyaktigheten til de forventede antallene, sammenlignet med det faktiske antallet.

MAPE er en enkel metrikkverdi. En 10% MAPE representerer at gjennomsnittsavviket mellom prognoseverdiene og de faktiske verdiene er 10%, uavhengig av om avviket var positivt eller negativt. Standarder for ønskelige MAPE-verdier varierer på tvers av bransjer.

Den lyseblå linjen i denne grafen representerer de faktiske salgsverdiene. Den mørkeblå linjen representerer prognoseverdiene for salg. Sammenligning av faktiske og prognoseerte salg viser at modellen effektivt forutsier salg for Furniture-kategorien i løpet av de første seks månedene av 2023.

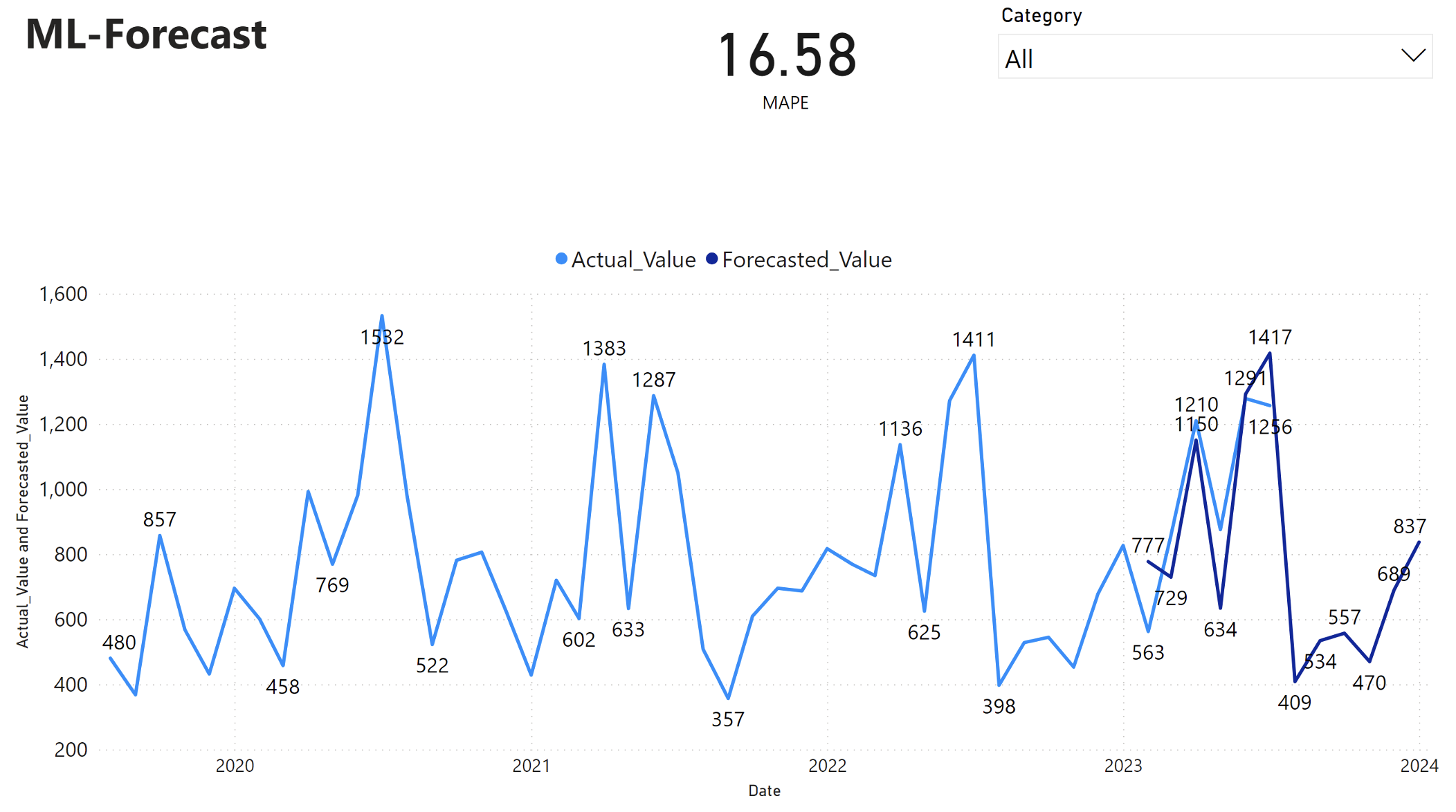
Skjermbilde av en Power BI-rapport.

Basert på denne observasjonen kan vi ha tillit til prognosefunksjonene til modellen, for det totale salget de siste seks månedene av 2023, og utvide til 2024. Denne tilliten kan informere strategiske beslutninger om lagerstyring, innkjøp av råvarer og andre forretningsrelaterte hensyn.

Relatert innhold