非アフィン変換

変換行列の 3 番目の列を使用して透視効果とテーパ効果を作成する

移動、スケーリング、回転、傾斜はすべてアフィン変換として分類されます。 アフィン変換は平行線を保持します。 変換の前に 2 つの線が平行である場合、これらは変換後も平行のままです。 四角形は常に平行四辺形に変換されます。

ただし、SkiaSharp は、四角形を任意の凸四角形に変換する機能を持つ非アフィン変換も実行できます。

凸四角形は、内部角度が常に 180 度未満で、辺が互いに交差しない 4 辺の図形です。

変換行列の第 3 行が 0、0、1 以外の値に設定されている場合、非アフィン変換が発生します。 完全な SKMatrix 乗算は次のとおりです。

              │ ScaleX  SkewY   Persp0 │
| x  y  1 | × │ SkewX   ScaleY  Persp1 │ = | x'  y'  z' |
              │ TransX  TransY  Persp2 │

変換結果の数式は次のとおりです。

x' = ScaleX·x + SkewX·y + TransX

y' = SkewY·x + ScaleY·y + TransY

z` = Persp0·x + Persp1·y + Persp2

2 次元変換に 3 対 3 行列を使用する基本的なルールは、Z が 1 である平面上にすべてが残っているということです。 Persp0 と Persp1 が 0 で、Persp2 が 1 でない限り、変換によって Z 座標がその平面から移動します。

これを 2 次元変換に復元するには、座標をその平面に戻す必要があります。 これには別の手順が必要です。 x'、y'、z' の値は z' で除算する必要があります。

x" = x' / z'

y" = y' / z'

z" = z' / z' = 1

これらは同次座標と呼ばれており、数学者のアウグスト・フェルディナント・メビウスによって構築されました。メビウスは、メビウスの帯という位相幾何学上の奇妙な現象の方がよく知られています。

z' が 0 である場合、除算の結果は無限座標になります。 実際に、メビウスが同次座標を構築した動機の 1 つは、有限数で無限の値を表す能力でした。

ただし、図表を表示する場合は、無限値に変換される座標を使用して何かをレンダリングしないようにする必要があります。 これらの座標はレンダリングされません。 これらの座標の近くにあるものはすべて非常に大きくなり、おそらく視覚的に一貫性がありません。

次の式では、z' の値が 0 にならないようにする必要があります。

z` = Persp0·x + Persp1·y + Persp2

したがって、これらの値にはいくつかの現実的な制限があります。

Persp2 セルは 0 である場合も 0 でない場合もあります。 Persp2 が 0 である場合、z' は点 (0, 0) に対して 0 であり、これは通常、望ましくありません。なぜなら、この点は 2 次元の図表では非常に一般的であるからです。 Persp2 が 0 と等しくない場合、Persp2 が1 に固定されているときに一般性は失われません。 たとえば、Persp2 を 5 にする必要があると判断した場合、行列内のすべてのセルを 5 で除算するだけで、Persp2 が 1 と等しくなり、結果は同じになります。

このような理由から、多くの場合、Persp2 は、単位行列内の同じ値である 1 で固定されます。

一般に、Persp0 と Persp1 は小さい数値です。 たとえば、単位行列から始めるが、Persp0 を 0.01 に設定するとします。

| 1  0   0.01 |
| 0  1    0   |
| 0  0    1   |

変換公式は次のとおりです。

x` = x / (0.01·x + 1)

y' = y / (0.01·x + 1)

ここで、この変換を使用して、原点に配置された 100 ピクセルの正方形のボックスをレンダリングします。 4 つの角の変換方法を次に示します。

(0, 0) → (0, 0)

(0, 100) → (0, 100)

(100, 0) → (50, 0)

(100, 100) → (50, 50)

x が 100 である場合、z' の分母は 2 であるため、x 座標と y 座標は実質的に半分になります。 ボックスの右側は、左側よりも短くなります。

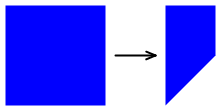
これらのセル名の Persp 部分は "遠近法" を表します。なぜなら、短縮法により、ボックスが右側が観察者から遠い状態で傾いていることが示されているためです。

[遠近法のテスト] ページでは、Persp0 と Pers1 の値を使用して実験し、これらの動作を確認できます。 これらの行列セルの適正値は非常に小さいため、ユニバーサル Windows プラットフォーム内の Slider では適切に処理できません。 UWP の問題に対応するには、TestPerspective.xaml の 2 つの Slider 要素を –1 から 1 の範囲に初期化する必要があります。

<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
             xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
             xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
             x:Class="SkiaSharpFormsDemos.Transforms.TestPerspectivePage"
             Title="Test Perpsective">
    <Grid>
        <Grid.RowDefinitions>
            <RowDefinition Height="Auto" />
            <RowDefinition Height="Auto" />
            <RowDefinition Height="Auto" />
            <RowDefinition Height="Auto" />
            <RowDefinition Height="*" />
        </Grid.RowDefinitions>

        <Grid.Resources>
            <ResourceDictionary>
                <Style TargetType="Label">
                    <Setter Property="HorizontalTextAlignment" Value="Center" />
                </Style>

                <Style TargetType="Slider">
                    <Setter Property="Minimum" Value="-1" />
                    <Setter Property="Maximum" Value="1" />
                    <Setter Property="Margin" Value="20, 0" />
                </Style>
            </ResourceDictionary>
        </Grid.Resources>

        <Slider x:Name="persp0Slider"
                Grid.Row="0"
                ValueChanged="OnPersp0SliderValueChanged" />

        <Label x:Name="persp0Label"
               Text="Persp0 = 0.0000"
               Grid.Row="1" />

        <Slider x:Name="persp1Slider"
                Grid.Row="2"
                ValueChanged="OnPersp1SliderValueChanged" />

        <Label x:Name="persp1Label"
               Text="Persp1 = 0.0000"
               Grid.Row="3" />

        <skia:SKCanvasView x:Name="canvasView"
                           Grid.Row="4"
                           PaintSurface="OnCanvasViewPaintSurface" />
    </Grid>
</ContentPage>

TestPerspectivePage 分離コード ファイル内のスライダーのイベント ハンドラーは、これらの値を 100 で除算して、-0.01 から 0.01 の範囲になるようにします。 さらに、コンストラクターはビットマップに読み込まれます。

public partial class TestPerspectivePage : ContentPage
{
    SKBitmap bitmap;

    public TestPerspectivePage()
    {
        InitializeComponent();

        string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
        Assembly assembly = GetType().GetTypeInfo().Assembly;

        using (Stream stream = assembly.GetManifestResourceStream(resourceID))
        {
            bitmap = SKBitmap.Decode(stream);
        }
    }

    void OnPersp0SliderValueChanged(object sender, ValueChangedEventArgs args)
    {
        Slider slider = (Slider)sender;
        persp0Label.Text = String.Format("Persp0 = {0:F4}", slider.Value / 100);
        canvasView.InvalidateSurface();
    }

    void OnPersp1SliderValueChanged(object sender, ValueChangedEventArgs args)
    {
        Slider slider = (Slider)sender;
        persp1Label.Text = String.Format("Persp1 = {0:F4}", slider.Value / 100);
        canvasView.InvalidateSurface();
    }
    ...
}

PaintSurface ハンドラーは、100 で除算されたこれら 2 つのスライダーの値に基づいて、perspectiveMatrix という名前の SKMatrix 値を計算します。 これは、この変換の中心をビットマップの中心に配置する 2 つの移動変換と組み合わされます。

public partial class TestPerspectivePage : ContentPage
{
    ...
    void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
    {
        SKImageInfo info = args.Info;
        SKSurface surface = args.Surface;
        SKCanvas canvas = surface.Canvas;

        canvas.Clear();

        // Calculate perspective matrix
        SKMatrix perspectiveMatrix = SKMatrix.MakeIdentity();
        perspectiveMatrix.Persp0 = (float)persp0Slider.Value / 100;
        perspectiveMatrix.Persp1 = (float)persp1Slider.Value / 100;

        // Center of screen
        float xCenter = info.Width / 2;
        float yCenter = info.Height / 2;

        SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
        SKMatrix.PostConcat(ref matrix, perspectiveMatrix);
        SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(xCenter, yCenter));

        // Coordinates to center bitmap on canvas
        float x = xCenter - bitmap.Width / 2;
        float y = yCenter - bitmap.Height / 2;

        canvas.SetMatrix(matrix);
        canvas.DrawBitmap(bitmap, x, y);
    }
}

いくつかのサンプル画像を次に示します。

スライダーを試すと、0.0066 を超える値または –0.0066 を下回る値が原因で、画像が突然歪み、首尾一貫しなくなることがわかります。 変換されるビットマップは 300 ピクセルの正方形です。 これは中心を基準にして変換されるため、ビットマップの座標の範囲は -150 から 150 になります。 z' の値は次の値であることを思い起こしてください。

z` = Persp0·x + Persp1·y + 1

Persp0 または Persp1 が 0.0066 を超えるか –0.0066 を下回る場合、z' の値が 0 になる原因となるビットマップの座標が常に存在します。 これが、0 による除算の原因となり、レンダリングが混乱します。 非アフィン変換を使用する場合、0 による除算の原因となる座標を含むレンダリングを回避する必要があります。

一般に、Persp0 と Persp1 を分離して設定することはありません。 また、多くの場合、行列内のその他のセルを設定し、特定の種類の非アフィン変換を実現する必要があります。

このような非アフィン変換の 1 つがテーパ変換です。 この種類の非アフィン変換は、四角形の全体の寸法を保持しますが、片側は先細りになります。

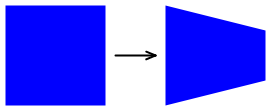
TaperTransform クラスは、次のパラメータに基づいて非アフィン変換の一般的な計算を実行します。

• 変換される画像の四角形のサイズ
• 先細りにする四角形の側面を示す列挙体
• 先細りする方法を示す別の列挙体
• 先細りの程度

のコードを次に示します。

enum TaperSide { Left, Top, Right, Bottom }

enum TaperCorner { LeftOrTop, RightOrBottom, Both }

static class TaperTransform
{
    public static SKMatrix Make(SKSize size, TaperSide taperSide, TaperCorner taperCorner, float taperFraction)
    {
        SKMatrix matrix = SKMatrix.MakeIdentity();

        switch (taperSide)
        {
            case TaperSide.Left:
                matrix.ScaleX = taperFraction;
                matrix.ScaleY = taperFraction;
                matrix.Persp0 = (taperFraction - 1) / size.Width;

                switch (taperCorner)
                {
                    case TaperCorner.RightOrBottom:
                        break;

                    case TaperCorner.LeftOrTop:
                        matrix.SkewY = size.Height * matrix.Persp0;
                        matrix.TransY = size.Height * (1 - taperFraction);
                        break;

                    case TaperCorner.Both:
                        matrix.SkewY = (size.Height / 2) * matrix.Persp0;
                        matrix.TransY = size.Height * (1 - taperFraction) / 2;
                        break;
                }
                break;

            case TaperSide.Top:
                matrix.ScaleX = taperFraction;
                matrix.ScaleY = taperFraction;
                matrix.Persp1 = (taperFraction - 1) / size.Height;

                switch (taperCorner)
                {
                    case TaperCorner.RightOrBottom:
                        break;

                    case TaperCorner.LeftOrTop:
                        matrix.SkewX = size.Width * matrix.Persp1;
                        matrix.TransX = size.Width * (1 - taperFraction);
                        break;

                    case TaperCorner.Both:
                        matrix.SkewX = (size.Width / 2) * matrix.Persp1;
                        matrix.TransX = size.Width * (1 - taperFraction) / 2;
                        break;
                }
                break;

            case TaperSide.Right:
                matrix.ScaleX = 1 / taperFraction;
                matrix.Persp0 = (1 - taperFraction) / (size.Width * taperFraction);

                switch (taperCorner)
                {
                    case TaperCorner.RightOrBottom:
                        break;

                    case TaperCorner.LeftOrTop:
                        matrix.SkewY = size.Height * matrix.Persp0;
                        break;

                    case TaperCorner.Both:
                        matrix.SkewY = (size.Height / 2) * matrix.Persp0;
                        break;
                }
                break;

            case TaperSide.Bottom:
                matrix.ScaleY = 1 / taperFraction;
                matrix.Persp1 = (1 - taperFraction) / (size.Height * taperFraction);

                switch (taperCorner)
                {
                    case TaperCorner.RightOrBottom:
                        break;

                    case TaperCorner.LeftOrTop:
                        matrix.SkewX = size.Width * matrix.Persp1;
                        break;

                    case TaperCorner.Both:
                        matrix.SkewX = (size.Width / 2) * matrix.Persp1;
                        break;
                }
                break;
        }
        return matrix;
    }
}

このクラスは、[テーパ変換] ページで使用されます。 XAML ファイルは、列挙値を選択するための 2 つの Picker 要素と、先細りの割合を選択するための Slider のインスタンスを作成します。 PaintSurface ハンドラーは、テーパ変換を 2 つの移動変換と組み合わせて、ビットマップの左上の角を基準に変換を行います。

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    TaperSide taperSide = (TaperSide)taperSidePicker.SelectedItem;
    TaperCorner taperCorner = (TaperCorner)taperCornerPicker.SelectedItem;
    float taperFraction = (float)taperFractionSlider.Value;

    SKMatrix taperMatrix =
        TaperTransform.Make(new SKSize(bitmap.Width, bitmap.Height),
                            taperSide, taperCorner, taperFraction);

    // Display the matrix in the lower-right corner
    SKSize matrixSize = matrixDisplay.Measure(taperMatrix);

    matrixDisplay.Paint(canvas, taperMatrix,
        new SKPoint(info.Width - matrixSize.Width,
                    info.Height - matrixSize.Height));

    // Center bitmap on canvas
    float x = (info.Width - bitmap.Width) / 2;
    float y = (info.Height - bitmap.Height) / 2;

    SKMatrix matrix = SKMatrix.MakeTranslation(-x, -y);
    SKMatrix.PostConcat(ref matrix, taperMatrix);
    SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(x, y));

    canvas.SetMatrix(matrix);
    canvas.DrawBitmap(bitmap, x, y);
}

次に例をいくつか示します。

一般化された非アフィン変換のもう 1 つの種類が 3D 回転です。これは、次の記事「3D 回転」で説明します。

非アフィン変換では、四角形を任意の凸四角形に変換できます。 これは、[非アフィン行列の表示] ページで示されています。 これは、「行列変換」記事の [アフィン行列の表示] ページによく似ていますが、ビットマップの 4 番目の角を操作する 4 番目の TouchPoint オブジェクトがあることを除きます。

ビットマップのいずれかの角の内部角度を 180 度より大きくしたり、2 つの辺を相互に交差させたりしない限り、ShowNonAffineMatrixPage クラスから次のメソッドを使用して変換が正常に計算されます。

static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL, SKPoint ptLR)
{
    // Scale transform
    SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);

    // Affine transform
    SKMatrix A = new SKMatrix
    {
        ScaleX = ptUR.X - ptUL.X,
        SkewY = ptUR.Y - ptUL.Y,
        SkewX = ptLL.X - ptUL.X,
        ScaleY = ptLL.Y - ptUL.Y,
        TransX = ptUL.X,
        TransY = ptUL.Y,
        Persp2 = 1
    };

    // Non-Affine transform
    SKMatrix inverseA;
    A.TryInvert(out inverseA);
    SKPoint abPoint = inverseA.MapPoint(ptLR);
    float a = abPoint.X;
    float b = abPoint.Y;

    float scaleX = a / (a + b - 1);
    float scaleY = b / (a + b - 1);

    SKMatrix N = new SKMatrix
    {
        ScaleX = scaleX,
        ScaleY = scaleY,
        Persp0 = scaleX - 1,
        Persp1 = scaleY - 1,
        Persp2 = 1
    };

    // Multiply S * N * A
    SKMatrix result = SKMatrix.MakeIdentity();
    SKMatrix.PostConcat(ref result, S);
    SKMatrix.PostConcat(ref result, N);
    SKMatrix.PostConcat(ref result, A);

    return result;
}

計算を容易にするために、このメソッドは、3 つの個別の変換の積として合計変換を取得します。ここでは、これらの変換によってビットマップの 4 つの角がどのように変更されるかを示すために矢印を使用して表されています。

(0, 0) → (0, 0) → (0, 0) → (x0, y0) (左上)

(0, H) → (0, 1) → (0, 1) → (x1, y1) (左下)

(W, 0) → (1, 0) → (1, 0) → (x2, y2) (右上)

(W, H) → (1, 1) → (a, b) → (x3, y3) (右下)

右側の最後の座標は、4 つの接触点に関連付けられた 4 つの点です。 これらは、ビットマップの角の最後の座標です。

W と H は、ビットマップの幅と高さを表します。 最初の変換 S は、ただ単にビットマップを 1 ピクセルの正方形にスケーリングします。 2 番目の変換は非アフィン変換 N で、3 番目はアフィン変換 A です。 このアフィン変換は 3 つの点に基づいているため、以前のアフィン ComputeMatrix メソッドと同じように、(a, b) 点を持つ 4 行目は含まれません。

3 番目の変換がアフィンになるように、a および b 値が計算されます。 このコードは、アフィン変換の逆関数を取得し、これを使用して右下の角をマップします。 それが点 (a, b) です。

非アフィン変換のもう 1 つの用途は、3 次元グラフィックスを模倣することです。 次の記事「3D 回転」では、3D 空間で 2 次元グラフィックを回転させる方法について説明します。

関連リンク

• SkiaSharp API