タイム シリーズ モデルのマイニング モデル コンテンツ (Analysis Services - データ マイニング)
すべてのマイニング モデルは同じ構造を使用してコンテンツを格納します。 この構造は、データ マイニング コンテンツ スキーマ行セットに従って定義されます。 しかし、その標準の構造の中で、情報を含むノードがさまざまな形で配置されて、さまざまな種類のツリーが表現されます。 このトピックでは、Microsoft Time Series アルゴリズムに基づくマイニング モデルのノードの編成方法と各ノードの意味について説明します。
すべてのモデルの種類に適用される一般的なマイニング モデル コンテンツの詳細については、「 マイニング モデル コンテンツ (Analysis Services - データ マイニング)」を参照してください。
このトピックは、タイム シリーズ モデルのコンテンツを参照しながら読むことをお勧めします。 タイム シリーズ モデルは、「基本的なデータ マイニング チュートリアル」を完了することによって作成できます。 このチュートリアルで作成するモデルは、ARIMA アルゴリズムと ARTXP アルゴリズムの両方を使用してデータをトレーニングする混合モデルです。 詳細については、「 予測構造とモデルの作成 (中間データ マイニング チュートリアル)」を参照してください。 マイニング モデルのコンテンツの表示方法の詳細については、「 データ マイニング モデル ビューアー」を参照してください。
タイム シリーズ モデルの構造について
タイム シリーズ モデルには、モデルとそのメタデータを表す 1 つの親ノードがあります。 その親ノードの下には、モデルの作成に使用したアルゴリズムに応じて 1 つまたは 2 つのタイム シリーズ ツリーがあります。
混合モデルを作成した場合は、ARIMA と ARTXP のそれぞれに 1 つずつ、2 つの個別のツリーがモデルに追加されます。 ARTXP または ARIMA のアルゴリズムのみを使用するように選択した場合は、そのアルゴリズムに対応する 1 つのツリーが含まれます。 どちらのアルゴリズムを使用するかは、FORECAST_METHOD パラメーターを設定して指定します。 ARTXP、ARIMA、または混合モデルのどれを使用するかについては、「 Microsoft Time Series アルゴリズム」を参照してください。
次の図は、既定の設定 (混合モデルが作成されます) を使用して作成したタイム シリーズ データ マイニング モデルの例を示しています。 ここでは、2 つのモデルの違いを比較しやすいように、図の左側に ARTXP モデルが、右側に ARIMA モデルが示されています。 ARTXP は、しだいに小さな分岐に分割されていくツリー状の構造であるのに対し、ARIMA アルゴリズムによって作成される構造はむしろ、小さな構成要素から積み上げられていくピラミッドに似ています。
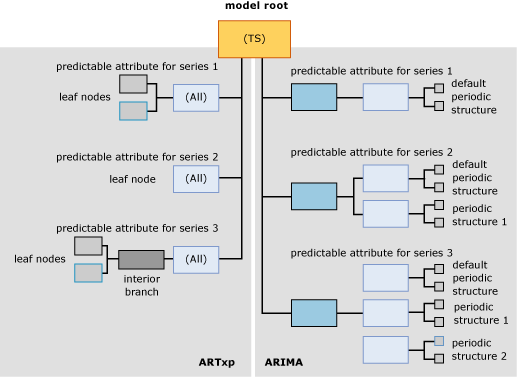
ここで重要な点は、ARIMA ツリーと ARTXP ツリーでは情報がまったく異なる形で配置されているということです。この 2 つのツリーが関連していると見なすことができるのはルート ノードだけです。 この 2 つの表現は、便宜上 1 つのモデルで提示されていますが、2 つの独立したモデルとして扱う必要があります。 ARTXP は実際のツリー構造を表しますが、ARIMA はそうではありません。
Microsoft 汎用コンテンツ ツリー ビューアーを使用して、ARIMA と ARTXP の両方を表示すると、ARTXP モデルと ARIMA モデルのすべてのノードが親タイム シリーズ モデルの子ノードとして表されます。 ただし、ノードのラベルで簡単にそれぞれを区別できます。
"(すべて)" というラベルが付いた最初のノードのセットが ARTXP アルゴリズムによる分析の結果を表します。
"ARIMA" というラベルが付いた 2 つ目のノードのセットが ARIMA アルゴリズムによる分析の結果を表します。
警告
ARTXP ツリーの "(すべて)" という名前は、旧バージョンとの互換性のためのみに保持されています。 SQL Server 2008 より前のバージョンのタイム シリーズ アルゴリズムでは、分析に使用されていたアルゴリズムは ARTXP アルゴリズム 1 つだけでした。
次のセクションでは、各種のモデルでのノードの配置方法について説明します。
ARTXP モデルの構造
ARTXP アルゴリズムでは、デシジョン ツリー モデルのようなモデルが作成されます。 予測可能な属性がグループ化され、大きな違いが見つかるたびに分割されます。 したがって、各 ARTXP モデルには、予測可能な属性ごとに個別の分岐が含まれます。 たとえば、「基本的なデータ マイニング チュートリアル」で作成する、複数の地域の売上高を予測するモデルでは、 予測可能な属性は [Amount] で、地域ごとに個別の分岐が作成されています。 [Amount] と [Quantity]という 2 つの予測可能な属性があった場合は、属性と地域の組み合わせごとに個別の分岐が作成されます。
ARTXP 分岐の最上位ノードには、デシジョン ツリーのルート ノードと同じ情報が含まれています (そのノードの子の数 (CHILDREN_CARDINALITY)、そのノードの条件を満たすケースの数 (NODE_SUPPORT)、および各種の記述統計 (NODE_DISTRIBUTION))。
ノードに子がない場合は、ケースをさらにサブグループに分割することを正当化するような重要な条件が見つからなかったことになります。 分岐はそこで終了し、そのノードを リーフ ノードと呼びます。 リーフ ノードには、ARTXP 式の構成要素である属性、係数、および値が含まれます。
デシジョン ツリー モデルのようにさらに分割される分岐もあります。 たとえば、ヨーロッパ地域の売上を表すツリーの分岐は 2 つの分岐に分割されています。 分割は、2 つのグループの間に大きな違いをもたらす条件が検出された場合に発生します。 親ノードからは、分割の原因となった属性の名前 ([Amount] など) と、親ノードのケースの数がわかります。 リーフ ノードでは、属性の値 ([Sales] >10,000 と [Sales] < 10,000 など)、各条件をサポートするケースの数、および ARTXP 数式の詳細が提供されます。
注意
式を表示するには、リーフ ノードのレベルで完全な回帰式を取得します。中間のノードやルート ノードでは取得できません。
ARIMA モデルの構造
ARIMA アルゴリズムは、データ系列 ( [Region]など) と予測可能な属性 ([ Sales Amount]など) の組み合わせごとに 1 つの情報を作成します。これは、時間の経過に伴う予測可能な属性の変化を表す式です。
各系列の式は、複数の構成要素から導き出されます。これらの構成要素は、データ内で検出された周期構造ごとに 1 つずつあります。 たとえば、1 か月ごとに収集される売上データがある場合には、月、四半期、年などの周期構造がアルゴリズムによって検出される可能性があります。
アルゴリズムは、検出された周期性ごとに別の親ノードと子ノードのセットを出力します。 既定の周期性である 1 (1 つのタイム スライス) は、すべてのモデルに自動的に追加されます。 PERIODICITY_HINT パラメーターに複数の値を入力することによって、考えられる周期構造を指定できます。 ただし、アルゴリズムによって周期構造が検出されなかった場合には、そのヒントの結果は出力されません。
モデル コンテンツに出力される各周期構造には、次のコンポーネント ノードが含まれています。
自己回帰の次数 (AR) のノード
移動平均 (MA) のノード
これらの用語の意味については、「 Microsoft Time Series アルゴリズム」を参照してください。
差分の次数 は数式の重要な一部であり、式で表されます。 差分の次数の使用方法の詳細については、「 Microsoft Time Series アルゴリズム テクニカル リファレンス」を参照してください。
タイム シリーズ モデルのモデル コンテンツ
ここでは、マイニング モデル コンテンツの列のうち、タイム シリーズ モデルに関連する列についてのみ詳細と例を紹介します。
スキーマ行セットの汎用列 (MODEL_CATALOGやMODEL_NAMEなど) の詳細、またはマイニング モデルの用語の説明については、「 マイニング モデル コンテンツ (Analysis Services - データ マイニング)」を参照してください。
MODEL_CATALOG
モデルが格納されているデータベースの名前。
MODEL_NAME
モデルの名前。
ATTRIBUTE_NAME
ノードで表されるデータ系列の予測可能な属性 (MSOLAP_MODEL_COLUMN と同じ値)。
NODE_NAME
ノード名。
現在、この列には NODE_UNIQUE_NAME と同じ値が格納されていますが、将来のリリースで変更される可能性があります。
NODE_UNIQUE_NAME
ノードの一意の名前。 モデルの親ノードの名前は常に TSになります。
ARTXP: 各ノードは、TS の後に 16 進数の数値を付けて表されます。 ノードの順序は重要ではありません。
たとえば、TS ツリーの直下の ARTXP ノードは TS00000001 ~ TS0000000b になります。
ARIMA: ARIMA ツリーの各ノードは、TA の後に 16 進数の数値を付けて表されます。 子ノードでは、親ノードの一意の名前の後に、ノード内のシーケンスを表すまた別の 16 進数が付きます。
すべての ARIMA ツリーの構造はまったく同じです。 各ルートに含まれるノードと名前付け規則の例を次の表に示します。
| ARIMA ノードの ID および種類 | ノード名の例 |
|---|---|
| ARIMA ルート (27) | TA0000000b |
| ARIMA 周期構造 (28) | TA0000000b00000000 |
| ARIMA 自己回帰 (29) | TA0000000b000000000 |
| ARIMA 移動平均 (30) | TA0000000b000000001 |
NODE_TYPE
タイム シリーズ モデルでは、アルゴリズムに応じて次のノードの種類が出力されます。
Artxp:
| ノードの種類の ID | 説明 |
|---|---|
| 1 (モデル) | タイム シリーズ |
| 3 (内部) | ARTXP タイム シリーズ ツリー内の内部分岐を表します。 |
| 16 (タイム シリーズ ツリー) | 予測可能な属性と系列に対応する ARTXP ツリーのルート。 |
| 15 (タイム シリーズ) | ARTXP ツリーのリーフ ノード。 |
有馬:
| ノードの種類の ID | 説明 |
|---|---|
| 27 (ARIMA ルート) | ARIMA ツリーの最上位ノード。 |
| 28 (ARIMA 周期構造) | 1 つの周期構造を表す ARIMA ツリーの構成要素。 |
| 29 (ARIMA 自己回帰) | 1 つの周期構造の係数が含まれています。 |
| 30 (ARIMA 移動平均) | 1 つの周期構造の係数が含まれています。 |
NODE_CAPTION
ノードに関連付けられているラベルまたはキャプション。
このプロパティは、主に表示を目的としています。
ARTXP: 属性と値の範囲の組み合わせとして表示されるノードの分割条件が含まれます。
ARIMA: ARIMA 式の短い形式が含まれます。
ARIMA 式の形式については、「 ARIMA 式のマイニング凡例」を参照してください。
CHILDREN_CARDINALITY
ノードの直接の子の数。
PARENT_UNIQUE_NAME
ノードの親の一意な名前です。 ルート レベルのノードには NULL を返します。
NODE_DESCRIPTION
現在のノードのルール、分割、または式の説明テキスト。
ARTXP: 詳細については、「 ARTXP ツリーについて」を参照してください。
ARIMA: 詳細については、「 ARIMA ツリーについて」を参照してください。
NODE_RULE
現在のノードのルール、分割、または式の XML 記述。
ARTXP: 通常は NODE_CAPTION と同じです。
ARIMA: 詳細については、「 ARIMA ツリーについて」を参照してください。
MARGINAL_RULE
そのノードに固有の分割またはコンテンツの XML 記述。
ARTXP: 通常は NODE_DESCRIPTION と同じです。
ARIMA: 常に空白です。代わりに NODE_RULE を使用します。
NODE_PROBABILITY
ARTXP: ツリー ノードの場合は常に 1 です。 リーフ ノードの場合は、モデル ルート ノードからそのノードに到達する確率です。
ARIMA: 常に 0 です。
MARGINAL_PROBABILITY
ARTXP: ツリー ノードの場合は常に 1 です。 リーフ ノードの場合は、直接の親ノードからそのノードに到達する確率です。
ARIMA: 常に 0 です。
NODE_DISTRIBUTION
ノードの確率ヒストグラムが含まれているテーブル。 タイム シリーズ モデルでは、実際の回帰式を組み立てるのに必要なすべての構成要素がこの入れ子になったテーブルに含まれます。
ARTXP ツリーのノード ディストリビューション テーブルの詳細については、「 ARTXP ツリーについて」を参照してください。
ARIMA ツリーのノード ディストリビューション テーブルの詳細については、「 ARIMA ツリーについて」を参照してください。
すべての定数やその他の構成要素を判読可能な形式で表示するには、 タイム シリーズ ビューアーを使用します。ノードをクリックして [マイニング凡例]を開くと表示されます。
NODE_SUPPORT
このノードをサポートするケースの数。
ARTXP:[(すべて)] ノードの場合は、分岐に含まれるタイム スライスの合計数を表します。
末端のノードの場合は、NODE_CAPTION によって表される範囲に含まれるタイム スライスの数を表します。 末端のノードのタイム スライスの数を合計すると、常に分岐の [(すべて)] ノードの NODE_SUPPORT 値になります。
ARIMA: 現在の周期構造をサポートするケースの数。 このサポートの値は、現在の周期構造のすべてのノードで繰り返し表示されます。
MSOLAP_MODEL_COLUMN
ノードで表されるデータ系列の予測可能な属性 (ATTRIBUTE_NAME と同じ値)。
MSOLAP_NODE_SCORE
ツリーまたは分割の情報の価値を特徴付ける数値。
ARTXP: 分割を含まないノードの場合、値は常に 0.0 です。 分割を含むノードの場合、値はその分割の興味深さのスコアを表します。
スコアリング 方法の詳細については、「 機能の選択 (データ マイニング)」を参照してください。
有馬: ARIMA モデルのベイジアン情報条件 (BIC) スコア。 その式に関連付けられているすべての ARIMA ノードで同じスコアが設定されます。
MSOLAP_NODE_SHORT_CAPTION
Artxp: NODE_DESCRIPTIONと同じ情報。
ARIMA: NODE_CAPTION と同じ情報 (ARIMA 式の短い形式)。
ARTXP ツリーについて
ARTXP モデルでは、線形のデータの領域と、他の要因で分割されるデータの領域とが明確に区別されています。 予測可能な属性の変化を独立変数の関数として直接表すことができる場合は、回帰式を計算してその関係が表現されます。
たとえば、ほとんどのデータ系列で時間と売上の間に直接的な相関関係がある場合は、各系列が 1 つのタイム シリーズ ツリー (NODE_TYPE =16) に含まれます。そこに各データ系列の子ノードは含まれず、回帰式のみが含まれます。 一方、関係が線形でない場合は、ARTXP タイム シリーズ ツリーがデシジョン ツリー モデルのように条件で子ノードに分割されます。 Microsoft 汎用コンテンツ ツリー ビューアー でモデル コンテンツを表示すると、どこで分割が発生し、傾向線にどのような影響を与えているかを確認できます。
この動作をよく理解するには、例として、「 基本的なデータ マイニング チュートリアル」で作成したタイム シリーズ モデルについて見てみましょう。 AdventureWorks データ ウェアハウスに基づくこのモデルでは、特に複雑なデータは使用されません。 ARTXP ツリーの分割の数は多くはありません。 ただし、この比較的単純なモデルでも、次の 3 種類の分割を見ることができます。
太平洋地域の [Amount] (金額) の傾向線が時間キーで分割されています。 時間キーでの分割は、特定の時点で傾向が変化していることを意味します。 傾向線が線形なのはある時点までで、それ以降は、曲線により別の形になります。 たとえば、あるタイム シリーズが 2002 年 8 月 6 日まで続き、それ以降は別のタイム シリーズが始まる場合などが考えられます。
北米地域の [Amount] (金額) の傾向線が別の変数で分割されています。 このケースでは、同じモデルのヨーロッパ地域の値に基づいて北米の傾向が分割されています。 つまり、ヨーロッパの値が変化すると北米の値も変化することがアルゴリズムによって検出されたことになります。
ヨーロッパ地域の傾向線が自身で分割されています。
では、それぞれの分割は何を意味するのでしょうか? モデル コンテンツから得られる情報を解釈するには、そのデータと、そのデータがビジネスのコンテキストにおいて持つ意味の深い理解が必要になります。
このモデルからは、北米地域とヨーロッパ地域の傾向の間に関連があるように見えますが、それは単に、ヨーロッパのデータ系列の方がエントロピが高いために北米の傾向が弱く見えるだけかもしれません。 あるいは、2 つのスコアに大きな違いはなく、北米より先にヨーロッパを計算したことによるただの偶然かもしれません。 それでも、データを調べてその相関関係が間違いかどうかを確認したり、他の要因が関係しているかどうかを調査したりする必要はあります。
時間キーでの分割は、線の傾きに統計的に有意な変化があったことを意味します。 これは、各範囲のサポートや、分割に必要なエントロピの計算などの数学的要因によって引き起こされたものと考えられます。 したがって、この分割は、現実世界におけるモデルの意味という観点からは興味深いものではないと言えます。 しかし、分割で示される期間を調べると、データに表れていない興味深い相関関係が見つかる場合もあります (その頃に開始された販売促進などのイベントがデータに影響を与えているなど)。
データにその他の属性が含まれていると、より興味深いツリーの分岐の例が見られる可能性が高くなります。 たとえば、気象情報を追跡して分析のための属性として使用すると、売上と天気の複雑な相互作用を表すさまざまなツリーの分割が見られる可能性があります。
要するに、データ マイニングは、興味の対象になりうる現象がどこで発生しているかについてのヒントを得るのには役立ちますが、その情報の価値をコンテキストの中で正確に解釈するためには、詳細な調査と、ビジネス ユーザーの専門知識が必要になります。
ARTXP のタイム シリーズ式の要素
ARTXP ツリーまたはブランチの完全な数式を表示するには、Microsoft Time Series Viewer のマイニング凡例を使用することをお勧めします。このビューアーでは、すべての定数が読み取り可能な形式で表示されます。
次のセクションで、式のサンプルを示して基本的な項について説明します。
ARTXP 式のマイニング凡例
次の例は、 [マイニング凡例]に表示されたモデルの一部の ARTXP 式を示しています。 この式を表示するには、まず、「基本的なデータ マイニング チュートリアル」で作成した [Forecasting] モデルを Microsoft タイム シリーズ ビューアーで開き、 [モデル] タブをクリックします。次に、R250: Europe データ系列のツリーを選択します。
この例で使用される式を表示するには、7/5/2003 以降のデータ系列を表すノードをクリックします。
ツリー ノードの式の例を次に示します。
Quantity = 21.322
-0.293 * Quantity(R250 North America,-7) + 0.069 * Quantity(R250 Europe,-1) + 0.023 *
Quantity(R250 Europe,-3) -0.142 * Quantity(R750 Europe,-8)
この例の値 21.322 は、式の次の要素の関数として予測された Quantity の値です。
たとえば、1 つの要素は Quantity(R250 北米,-7) です。 これは、t-7 (現在のタイム スライスより 7 つ前のタイム スライス) における北米地域の数量を表しています。 上の式では、このデータ系列の値に係数 -0.293 が乗算されています。 各要素の係数は、トレーニング処理の間にデータの傾向に基づいて導き出されます。
この式に複数の要素があるのは、モデルによって、ヨーロッパ地域における R250 モデルの数量が他のいくつかのデータ系列の値に依存していると計算されたためです。
ARTXP 式のモデル コンテンツ
次の表は、 Microsoft 汎用コンテンツ ツリー ビューアー (データ マイニング) に表示される関連ノードの内容を使用して、数式と同じ情報を示しています。
| ATTRIBUTE_NAME | ATTRIBUTE_VALUE | SUPPORT | PROBABILITY | variance | VALUETYPE |
|---|---|---|---|---|---|
| Quantity(R250 Europe,y-intercept) | 21.3223433563772 | 11 | 0 | 1.65508795539661 | 11 (Intercept: 切片) |
| Quantity(R250 Europe,-1) | 0.0691694140876526 | 0 | 0 | 0 | 7 (Coefficient: 係数) |
| Quantity(R250 Europe,-1) | 20.6363635858123 | 0 | 0 | 182.380682874818 | 9 (Statistics: 統計) |
| Quantity(R750 Europe,-8) | -0.1421203048299 | 0 | 0 | 0 | 7 (Coefficient: 係数) |
| Quantity(R750 Europe,-8) | 22.5454545333019 | 0 | 0 | 104.362130048408 | 9 (Statistics: 統計) |
| Quantity(R250 Europe,-3) | 0.0234095979448281 | 0 | 0 | 0 | 7 (Coefficient: 係数) |
| Quantity(R250 Europe,-3) | 24.8181818883176 | 0 | 0 | 176.475304989169 | 9 (Statistics: 統計) |
| Quantity(R250 North America,-7) | -0.292914186039869 | 0 | 0 | 0 | 7 (Coefficient: 係数) |
| Quantity(R250 North America,-7) | 10.36363640433 | 0 | 0 | 701.882534898676 | 9 (Statistics: 統計) |
これらの例を比較するとわかりますが、マイニング モデル コンテンツには、 [マイニング凡例]に表示されるのと同じ情報が含まれていますが、その他に、 分散 と サポートの追加の列があります。 サポートの値は、この式によって表される傾向をサポートするケースの数を表します。
ARTXP のタイム シリーズ式の使用
ほとんどのビジネス ユーザーにとって、ARTXP モデル コンテンツの価値は、ツリー ビューとデータの線形表現の両方が組み合わされていることにあります。
予測可能な属性の変化を独立変数の線形関数として表現できる場合は、自動的に回帰式が計算されて、その系列が別のノードに出力されます。
リレーションシップを線形相関として表せない場合は、デシジョン ツリーのように分岐が生成されます。
Microsoft タイム シリーズ ビューアー でモデル コンテンツを参照すると、どこで分割が発生し、傾向線にどのような影響を与えているかを確認できます。
時間と売上の間に直接的な相関関係があるデータ系列の部分の式を取得するには、 [マイニング凡例]から式をコピーして、モデルの説明に使用するドキュメントやプレゼンテーションに貼り付けるのが最も簡単です。 あるいは、そのツリーの NODE_DISTRIBUTION テーブルから平均や係数などの情報を抽出して、それを使用してその傾向の延長を計算することもできます。 式は、系列全体が一貫した線形の関係を示している場合は (すべて) ノードに含まれ、 ツリーに分岐がある場合はリーフ ノードに含まれます。
次のクエリは、マイニング モデルのすべての ARTXP リーフ ノードを、式を含む入れ子になったテーブル NODE_DISTRIBUTION と共に返します。
SELECT MODEL_NAME, ATTRIBUTE_NAME, NODE_NAME,
NODE_CAPTION,
(SELECT ATTRIBUTE_NAME, ATTRIBUTE_VALUE, [VARIANCE], VALUETYPE
FROM NODE_DISTRIBUTION) as t
FROM Forecasting.CONTENT
WHERE NODE_TYPE = 15
ARIMA ツリーについて
ARIMA モデル内の各構造は、それぞれが 1 つの 周期性 ( 周期構造) に対応しています。 周期構造とは、データ系列全体で繰り返されるデータのパターンです。 パターンの小さな変化は、統計的な制限の範囲内で許容されます。 周期性は、データのトレーニングに使用された既定の時間単位に従って測定されます。 たとえば、トレーニング データが毎日の売上データの場合は、既定の時間単位が 1 日になり、すべての周期構造が日数で定義されます。
アルゴリズムによって検出された各周期にそれぞれ固有の構造ノードが割り当てられます。 たとえば、毎日の売上データを分析していて、週を表す周期構造がモデルによって検出された場合、 この場合、アルゴリズムは、完成したモデルに 2 つの周期構造を作成します。1 つは既定の日単位の期間で、もう 1 つは として示 {1}され、もう 1 つは で示される {7}週です。
たとえば、次のクエリは、マイニング モデルのすべての ARIMA 構造を返します。
SELECT MODEL_NAME, ATTRIBUTE_NAME, NODE_NAME, NODE_CAPTION
FROM Forecasting.CONTENT
WHERE NODE_TYPE = 27
結果の例:
| MODEL_NAME | ATTRIBUTE_NAME | NODE_NAME | NODE_TYPE | NODE_CAPTION |
|---|---|---|---|---|
| 予測 | M200 Europe:Quantity | TA00000000 | 27 | ARIMA (1,0,1) |
| 予測 | M200 North America:Quantity | TA00000001 | 27 | ARIMA (1,0,4) X (1,1,4)(6) |
| 予測 | M200 Pacific:Quantity | TA00000002 | 27 | ARIMA (2,0,8) X (1,0,0)(4) |
| 予測 | M200 Pacific:Quantity | TA00000002 | 27 | ARIMA (2,0,8) X (1,0,0)(4) |
| 予測 | R250 Europe:Quantity | TA00000003 | 27 | ARIMA (1,0,7) |
| 予測 | R250 North America:Quantity | TA00000004 | 27 | ARIMA (1,0,2) |
| 予測 | R250 Pacific:Quantity | TA00000005 | 27 | ARIMA (2,0,2) X (1,1,2)(12) |
| 予測 | R750 Europe:Quantity | TA00000006 | 27 | ARIMA (2,1,1) X (1,1,5)(6) |
| 予測 | T1000 Europe:Quantity | TA00000009 | 27 | ARIMA (1,0,1) |
| 予測 | T1000 North America:Quantity | TA0000000a | 27 | ARIMA (1,1,1) |
| 予測 | T1`000 Pacific:Quantity | TA0000000b | 27 | ARIMA (1,0,3) |
これらの結果から、 Microsoft 汎用コンテンツ ツリー ビューアー (データ マイニング) を使用して参照することもできます。どの系列が完全に線形であるか、複数の周期構造を持ち、検出された周期性が何であるかを一目で確認できます。
たとえば、M200 Europe 系列の ARIMA 式の短い形式からは、既定の周期 (1 日) のみが検出されたことがわかります。 式の短い形式は NODE_CAPTION 列に含まれています。
一方、M200 North America 系列では、追加の周期構造が検出されています。 ノード TA00000001 には、式 (1,0,4) を含むノードと式 (1,1,4)(6) を含むノードの 2 つの子ノードがあります。 これらの式は連結されて親ノードに表示されます。
このほか、モデル コンテンツには、各周期構造の 次数 と 移動平均 も子ノードとして含まれています。 たとえば、次のクエリは、上の例に示されている 1 つのノードの子ノードを取得します。 PARENT_UNIQUE_NAME という列は、同名の予約済みキーワードと区別するために角かっこで囲む必要があります。
SELECT *
FROM Forecasting.CONTENT
WHERE [PARENT_UNIQUE_NAME] = ' TA00000001'
これは ARTXP ツリーではなく ARIMA ツリーであるため、 IsDescendant (DMX) 関数を使用して、この周期構造の子ノードを返すことはできません。 代わりに、属性とノードの種類を使用して結果をフィルター処理します。これにより、式がどのように作成されたかについての詳細情報 (移動平均や差分の次数など) を含む子ノードを取得できます。
SELECT MODEL_NAME, ATTRIBUTE_NAME, NODE_UNIQUE_NAME,
NODE_TYPE, NODE_CAPTION
FROM Forecasting.CONTENT
WHERE [MSOLAP_MODEL_COLUMN] ='M200 North America:Quantity'
AND (NODE_TYPE = 29 or NODE_TYPE = 30)
結果の例:
| MODEL_NAME | ATTRIBUTE_NAME | NODE_UNIQUE_NAME | NODE_TYPE | NODE_CAPTION |
|---|---|---|---|---|
| 予測 | M200 North America:Quantity | TA00000001000000010 | 29 | ARIMA {1,0.961832044807041} |
| 予測 | M200 North America:Quantity | TA00000001000000011 | 30 | ARIMA {1,-3.51073103693271E-02,2.15731642954099,-0.220314343327742,-1.33151478258758} |
| 予測 | M200 North America:Quantity | TA00000001000000000 | 29 | ARIMA {1,0.643565911081657} |
| 予測 | M200 North America:Quantity | TA00000001000000001 | 30 | ARIMA {1,1.45035399809581E-02,-4.40489283927752E-02,-0.19203901352577,0.242202497643993} |
これらの例から、ARIMA ツリーをドリル ダウンするとさらに詳しい情報が得られることがわかります。ただし、重要な情報は結合されて親ノードにも表示されます。
ARIMA のタイム シリーズ式
ARIMA ノードの完全な式を表示するには、 Microsoft タイム シリーズ ビューアー の [マイニング凡例]を使用することをお勧めします。これにより、自己回帰の次数や移動平均などの式の要素を、一貫した形式で表示できます。
ここでは、式のサンプルを示して基本的な項について説明します。
ARIMA 式のマイニング凡例
次の例は、マイニング凡例に表示されたモデルの一部の ARIMA 式を示しています。 この式を表示するには、まず、 Microsoft タイム シリーズ ビューアー を使用して Forecastingモデルを開き、 [モデル] タブをクリックします。次に、 R250: Europe データ系列のツリーを選択し、7/5/2003 以降のデータ系列を表すノードをクリックします。 マイニング凡例では、次の例のように、すべての定数が判読可能な形式で表示されます。
ARIMA 式:
ARIMA ({1,1},{1,1,1.49791920964142,1.106400534999397,0.888873034670339,-5.05429403071953E-5 02,-0.905265316720334,-0.96190890064379,-0.649991020901922}) Intercept:56.88888888889
この式は、係数や切片の値を含む長い ARIMA 形式です。 この式の短い形式は になります {1,0,7}。ここで、1 は期間をタイム スライスの数として示し、0 は用語の差の順序を示し、7 は係数の数を示します。
注意
定数は、分散を算出するために Analysis Services によって計算されますが、その定数自体はユーザー インターフェイスには表示されません。 ただし、 [グラフ] ビューで [偏差の表示] を選択すると、系列内の任意のポイントの分散をこの定数の関数として表示することができます。 各データ系列のツールヒントに、予測された特定のポイントの分散が表示されます。
ARIMA 式のモデル コンテンツ
ARIMA モデルは、さまざまな種類のノードにさまざまな情報が含まれる標準の構造に従っています。 ARIMA モデルのモデル コンテンツを表示するには、ビューアーを Microsoft 汎用コンテンツ ツリー ビューアーに変更し、 R250 Europe: Quantityという属性名を持つノードを展開します。
データ系列の ARIMA モデルには、基本的な周期の式が、アプリケーションに応じて選択できる 4 つの異なる形式で含まれています。
NODE_CAPTION: 式の短い形式が表示されます。 この短い形式からは、表現されている周期構造の数と、その係数の数がわかります。 たとえば、式の短い形式が {4,0,6}である場合、ノードは係数が 6 である 1 つの周期構造を表します。 短い形式が x {1,0,0}(4) のようなもの{2,0,8}の場合、ノードには 2 つの周期構造が含まれます。
NODE DESCRIPTION: 式の長い形式が表示されます。これは、 [マイニング凡例]に表示される式の形式でもあります。 式の長い形式は短い形式に似ていますが、係数の数の代わりに実際の係数の値が表示される点が異なります。
NODE_RULE: 式の XML 表現が表示されます。 XML 表現には、ノードの種類に応じて 1 つまたは複数の周期構造が含まれます。 次の表は、XML ノードが ARIMA モデルの上位レベルにロール アップされるしくみを示しています。
| ノードの種類 | XML コンテンツ |
|---|---|
| 27 (ARIMA ルート) | データ系列のすべての周期構造と、各周期構造のすべての子ノードのコンテンツが含まれます。 |
| 28 (ARIMA 周期構造) | 1 つの周期構造を定義します。自己回帰の項のノードと移動平均の係数も含まれます。 |
| 29 (ARIMA 自己回帰) | 1 つの周期構造の項が一覧表示されます。 |
| 30 (ARIMA 移動平均) | 1 つの周期構造の係数が一覧表示されます。 |
NODE_DISTRIBUTION: 入れ子になったテーブルに式の項が表示されます。このテーブルに対してクエリを実行することにより、特定の項を取得できます。 ノード ディストリビューション テーブルは XML ルールと同じ階層構造に従っているため、 ARIMA 系列のルート ノード (NODE_TYPE = 27) には切片の値と完全な式の周期性 (複数の周期性が含まれる場合もあります) が含まれ、子ノードには特定の周期構造やその周期構造の子ノードに固有の情報のみが含まれます。
| ノードの種類 | 属性 | 値の型 |
|---|---|---|
| 27 (ARIMA ルート) | Intercept Periodicity |
11 |
| 28 (ARIMA 周期構造) | Periodicity 自己回帰の次数 Difference order Moving average order |
12 13 15 14 |
| 29 (ARIMA 自己回帰) | Coefficient (係数の補数) |
7 |
| 30 (ARIMA 移動平均) | t の値 t-1 の値 ... t-n の値 |
7 |
移動平均の次数 の値は、系列の移動平均の数を表します。 一般に、移動平均は、系列に n 個の項がある場合は n から 1 回計算されますが、計算を容易にするために数値を減らすことができます。
自己回帰の次数 の値は、自己回帰系列の数を表します。
差分の次数 の値は、系列が比較 (区別) される回数を表します。
使用可能な値型の列挙については、「 Microsoft.AnalysisServices.AdomdServer.MiningValueType」を参照してください。
ARIMA ツリーの情報の使用
ARIMA アルゴリズムに基づく予測をビジネス ソリューションで使用する場合は、レポートに式を貼り付けて、その予測の作成に使用された方法を示すことができます。 式を短い形式で提示するにはキャプションを、長い形式で提示するには説明を使用します。
タイム シリーズ予測を使用するアプリケーションを開発する場合は、モデル コンテンツから ARIMA 式を取得して独自に予測を行うこともできます。 特定の出力の ARIMA 式を取得するには、先の例で示したように、ARIMA ルートに対して直接その属性のクエリを実行します。
必要な系列を含むノードの ID がわかる場合は、次の 2 つの方法で式の構成要素を取得できます。
入れ子になったテーブルの形式 : DMX クエリを使用するか、OLEDB クライアントからクエリを実行します。
XML 表現: XML クエリを使用します。
解説
ARTXP ツリーでは、各分割の情報がそれぞれツリーの異なる場所にあるため、情報を取得するのが困難な場合があります。 したがって ARTXP モデルでは、すべての断片を取得してから、なんらかの処理を行って完全な式を再構成する必要があります。 ARIMA モデルでは、ツリー全体で式を取得できるようになっているため、比較的簡単に式を取得できます。 この情報を取得するクエリの作成方法については、「 タイム シリーズ モデルのクエリ例」を参照してください。
参照
Mining Model Content (Analysis Services - Data Mining)
Microsoft Time Series アルゴリズム
Time Series Model Query Examples
Microsoft タイム シリーズ アルゴリズム テクニカル リファレンス