Condividi tramite

Sviluppare, valutare e assegnare un punteggio a un modello di previsione per le vendite superstore

  • Articolo

Questa esercitazione presenta un esempio end-to-end di un flusso di lavoro di data science di Synapse in Microsoft Fabric. Lo scenario crea un modello di previsione che usa dati storici sulle vendite per stimare le vendite delle categorie di prodotti in un superstore.

La previsione è un asset fondamentale nelle vendite. Combina i dati storici e i metodi predittivi per fornire informazioni dettagliate sulle tendenze future. Le previsioni possono analizzare le vendite passate per identificare i modelli e apprendere dal comportamento dei consumatori per ottimizzare le strategie di inventario, produzione e marketing. Questo approccio proattivo migliora l'adattabilità, la velocità di risposta e le prestazioni complessive delle aziende in un marketplace dinamico.

L'esercitazione illustra questi passaggi:

  • Caricare i dati
  • Usare l'analisi esplorativa dei dati per comprendere ed elaborare i dati
  • Eseguire il training di un modello di Machine Learning con un pacchetto di software open-source e tenere traccia degli esperimenti con MLflow e la funzionalità di registrazione automatica di Fabric
  • Salvare il modello di Machine Learning finale ed eseguire previsioni
  • Visualizzare le prestazioni del modello con le visualizzazioni di Power BI

Prerequisiti

Seguire la procedura in un notebook

È possibile scegliere una di queste opzioni per seguire la procedura in un notebook:

  • Aprire ed eseguire il notebook predefinito nell'esperienza di data science di Synapse
  • Caricare il notebook da GitHub nell'esperienza di data science di Synapse

Aprire il notebook predefinito

Il notebook di esempio previsioni vendite accompagna questa esercitazione.

Per aprire il notebook di esempio predefinito dell'esercitazione nell'esperienza di data science di Synapse:

  1. Andare sulla pagina iniziale di data science di Synapse.

  2. Selezionare Usa un esempio.

  3. Selezionare l'esempio corrispondente:

    • Dalla scheda predefinita Flussi di lavoro end-to-end (Python), se l'esempio è relativo a un'esercitazione su Python.
    • Dalla scheda Flussi di lavoro end-to-end (R), se l'esempio è relativo a un'esercitazione su R.
    • Dalla scheda Esercitazioni rapide, se l'esempio è per un'esercitazione rapida.

  4. Collegare un lakehouse al notebook prima di iniziare a eseguire il codice.

Importare il notebook da GitHub

Il notebook di esempio AIsample - Superstore Forecast.ipynb accompagna questa esercitazione.

Per aprire il notebook di accompagnamento per questa esercitazione, seguire le istruzioni riportate in Preparare il sistema per le esercitazioni di data science per importare il notebook nell'area di lavoro.

Se si preferisce copiare e incollare il codice da questa pagina, è possibile creare un nuovo notebook.

Assicurarsi di collegare un lakehouse al notebook prima di iniziare a eseguire il codice.

Passaggio 1: caricare i dati

Il set di dati contiene 9.995 istanze di vendite di vari prodotti. Include anche 21 attributi. Questa tabella proviene dal file Superstore.xlsx usato in questo notebook:

ID riga ID ordine Data ordine Ship Date Ship Mode ID cliente Nome cliente Segmento Country City Provincia CAP Paese ID prodotto Categoria Sottocategoria Nome prodotto Vendite Quantità Sconto Margine
4 US-2015-108966 2015-10-11 2015-10-18 Classe Standard SO-20335 Sean O'Donnell Utente Stati Uniti Fort Lauderdale Florida 33311 South FUR-TA-10000577 Mobilio Tabelle Bretford CR4500 Series Slim Rectangular Table 957,5775 5 0,45 -383,0310
11 CA-2014-115812 2014-06-09 2014-06-09 Classe Standard Classe Standard Brosina Hoffman Utente Stati Uniti Los Angeles California 90032 West FUR-TA-10001539 Mobilio Tabelle Chromcraft Rectangular Conference Tables 1706,184 9 0,2 85,3092
31 US-2015-150630 2015-09-17 2015-09-21 Classe Standard TB-21520 Tracy Blumstein Utente Stati Uniti Filadelfia Pennsylvania 19140 East OFF-EN-10001509 Forniture di ufficio Buste Buste con legatura in corda di polietilene 3,264 2 0,2 1,1016

Definire questi parametri, in modo da poter usare questo notebook con set di dati diversi:

IS_CUSTOM_DATA = False  # If TRUE, the dataset has to be uploaded manually

IS_SAMPLE = False  # If TRUE, use only rows of data for training; otherwise, use all data
SAMPLE_ROWS = 5000  # If IS_SAMPLE is True, use only this number of rows for training

DATA_ROOT = "/lakehouse/default"
DATA_FOLDER = "Files/salesforecast"  # Folder with data files
DATA_FILE = "Superstore.xlsx"  # Data file name

EXPERIMENT_NAME = "aisample-superstore-forecast"  # MLflow experiment name

Scaricare il set di dati e caricarlo nel lakehouse

Questo codice scarica una versione disponibile pubblicamente del set di dati, quindi la archivia in un lakehouse di Fabric:

Importante

Assicurarsi di aggiungere un lakehouse al notebook prima di eseguirlo. In caso contrario, verrà visualizzato un errore.

import os, requests
if not IS_CUSTOM_DATA:
    # Download data files into the lakehouse if they're not already there
    remote_url = "https://synapseaisolutionsa.blob.core.windows.net/public/Forecast_Superstore_Sales"
    file_list = ["Superstore.xlsx"]
    download_path = "/lakehouse/default/Files/salesforecast/raw"

    if not os.path.exists("/lakehouse/default"):
        raise FileNotFoundError(
            "Default lakehouse not found, please add a lakehouse and restart the session."
        )
    os.makedirs(download_path, exist_ok=True)
    for fname in file_list:
        if not os.path.exists(f"{download_path}/{fname}"):
            r = requests.get(f"{remote_url}/{fname}", timeout=30)
            with open(f"{download_path}/{fname}", "wb") as f:
                f.write(r.content)
    print("Downloaded demo data files into lakehouse.")

Configurare il rilevamento dell'esperimento di MLflow

Microsoft Fabric acquisisce automaticamente i valori dei parametri di input e le metriche di output di un modello di Machine Learning durante il training. Questo estende le funzionalità di registrazione automatica di MLflow. Le informazioni vengono quindi registrate nell'area di lavoro, in cui è possibile accedervi e visualizzarle con le API MLflow o l'esperimento corrispondente nell'area di lavoro. Per altre informazioni sulla registrazione automatica, vedere Registrazione automatica in Microsoft Fabric.

Per spegnere la registrazione automatica di Microsoft Fabric in una sessione del notebook, chiamare mlflow.autolog() e impostare disable=True:

# Set up MLflow for experiment tracking
import mlflow

mlflow.set_experiment(EXPERIMENT_NAME)
mlflow.autolog(disable=True)  # Turn off MLflow autologging

Leggere i dati non elaborati dal lakehouse

Leggere i dati non elaborati dalla sezione File del lakehouse. Aggiungere altre colonne per parti di data diverse. Le stesse informazioni vengono usate per creare una tabella delta partizionata. Poiché i dati non elaborati vengono archiviati come file di Excel, è necessario usare Pandas per leggerli:

import pandas as pd
df = pd.read_excel("/lakehouse/default/Files/salesforecast/raw/Superstore.xlsx")

Passaggio 2: eseguire l'analisi esplorativa dei dati

Importare le librerie

Prima di qualsiasi analisi, importare le librerie necessarie:

# Importing required libraries
import warnings
import itertools
import numpy as np
import matplotlib.pyplot as plt
warnings.filterwarnings("ignore")
plt.style.use('fivethirtyeight')
import pandas as pd
import statsmodels.api as sm
import matplotlib
matplotlib.rcParams['axes.labelsize'] = 14
matplotlib.rcParams['xtick.labelsize'] = 12
matplotlib.rcParams['ytick.labelsize'] = 12
matplotlib.rcParams['text.color'] = 'k'
from sklearn.metrics import mean_squared_error,mean_absolute_percentage_error

Visualizzare i dati non elaborati

Esaminare manualmente un sottoinsieme dei dati per comprendere meglio il set di dati stesso e usare la funzione display per stampare il DataFrame. Inoltre, le viste Chart possono visualizzare facilmente i sottoinsiemi del set di dati.

display(df)

Questo notebook è incentrato principalmente sulla previsione delle vendite della categoria Furniture. Ciò accelera il calcolo e consente di visualizzare le prestazioni del modello. Tuttavia, questo notebook usa tecniche adattabili. È possibile estendere queste tecniche per stimare le vendite di altre categorie di prodotti.

# Select "Furniture" as the product category
furniture = df.loc[df['Category'] == 'Furniture']
print(furniture['Order Date'].min(), furniture['Order Date'].max())

Pre-elaborare i dati

Gli scenari aziendali reali spesso devono prevedere le vendite in tre categorie distinte:

  • Una categoria di prodotti specifica
  • Una categoria di clienti specifica
  • Una combinazione specifica di categoria di prodotti e categoria di clienti

Prima di tutto, eliminare le colonne non necessarie per pre-elaborare i dati. Alcune colonne (Row ID, Order ID,Customer ID e Customer Name) non sono necessarie perché non hanno alcun impatto. Si vuole prevedere le vendite complessive, nello stato e nell'area, per una categoria di prodotto specifica (Furniture), in modo da poter eliminare le colonne State, Region, Country, Citye Postal Code. Per prevedere le vendite per una località o una categoria specifica, potrebbe essere necessario modificare il passaggio di pre-elaborazione di conseguenza.

# Data preprocessing
cols = ['Row ID', 'Order ID', 'Ship Date', 'Ship Mode', 'Customer ID', 'Customer Name', 
'Segment', 'Country', 'City', 'State', 'Postal Code', 'Region', 'Product ID', 'Category', 
'Sub-Category', 'Product Name', 'Quantity', 'Discount', 'Profit']
# Drop unnecessary columns
furniture.drop(cols, axis=1, inplace=True)
furniture = furniture.sort_values('Order Date')
furniture.isnull().sum()

Il set di dati è strutturato su base giornaliera. È necessario ricampionare nella colonna Order Date, perché si vuole sviluppare un modello per prevedere le vendite su base mensile.

Prima di tutto, raggruppare la categoria Furniture in base a Order Date. Calcolare quindi la somma della colonna Sales per ogni gruppo per determinare le vendite totali per ogni valore univoco Order Date. Ricampionare la colonna Sales con la frequenza MS per aggregare i dati per mese. Infine, calcolare il valore medio delle vendite per ogni mese.

# Data preparation
furniture = furniture.groupby('Order Date')['Sales'].sum().reset_index()
furniture = furniture.set_index('Order Date')
furniture.index
y = furniture['Sales'].resample('MS').mean()
y = y.reset_index()
y['Order Date'] = pd.to_datetime(y['Order Date'])
y['Order Date'] = [i+pd.DateOffset(months=67) for i in y['Order Date']]
y = y.set_index(['Order Date'])
maximim_date = y.reset_index()['Order Date'].max()

Illustrare l'impatto di Order Date su Sales per la categoria Furniture:

# Impact of order date on the sales
y.plot(figsize=(12, 3))
plt.show()

Prima di qualsiasi analisi statistica, è necessario importare il modulo Python statsmodels. Fornisce classi e funzioni per la stima di molti modelli statistici. Fornisce inoltre classi e funzioni per eseguire test statistici ed esplorazione statistica dei dati.

import statsmodels.api as sm

Eseguire l'analisi statistica

Una serie temporale tiene traccia di questi elementi dati a intervalli impostati, per determinare la variazione di tali elementi nel modello serie temporale:

  • Livello: componente fondamentale che rappresenta il valore medio per un periodo di tempo specifico

  • Tendenza: descrive se la serie temporale diminuisce, rimane costante o aumenta nel tempo

  • Stagionalità: descrive il segnale periodico nella serie temporale e cerca occorrenze cicliche che influiscono sui modelli di serie temporali crescenti o decrescenti

  • Rumore/residuo: si riferisce alle fluttuazioni casuali e alla variabilità nei dati delle serie temporali che il modello non può spiegare.

In questo codice si osservano gli elementi per il set di dati dopo la pre-elaborazione:

# Decompose the time series into its components by using statsmodels
result = sm.tsa.seasonal_decompose(y, model='additive')

# Labels and corresponding data for plotting
components = [('Seasonality', result.seasonal),
              ('Trend', result.trend),
              ('Residual', result.resid),
              ('Observed Data', y)]

# Create subplots in a grid
fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(12, 7))
plt.subplots_adjust(hspace=0.8)  # Adjust vertical space
axes = axes.ravel()

# Plot the components
for ax, (label, data) in zip(axes, components):
    ax.plot(data, label=label, color='blue' if label != 'Observed Data' else 'purple')
    ax.set_xlabel('Time')
    ax.set_ylabel(label)
    ax.set_xlabel('Time', fontsize=10)
    ax.set_ylabel(label, fontsize=10)
    ax.legend(fontsize=10)

plt.show()

I tracciati descrivono la stagionalità, le tendenze e il rumore nei dati di previsione. È possibile acquisire i modelli sottostanti e sviluppare modelli che eseguono previsioni accurate resilienti alle fluttuazioni casuali.

Passaggio 3: eseguire il training e tenere traccia del modello

Dopo aver ottenuto i dati disponibili, definire il modello di previsione. In questo notebook applicare il modello di previsione denominato seasonal autoregressive integrated moving average with exogenous factors (SARIMAX). SARIMAX combina componenti autoregressive (AR) e della media mobile (MA), differenze stagionali e predittori esterni per effettuare previsioni accurate e flessibili per i dati delle serie temporali.

È anche possibile usare MLflow e la registrazione automatica di Fabric per tenere traccia degli esperimenti. Qui caricare la tabella delta dal lakehouse. È possibile usare altre tabelle delta che considerano il lakehouse come origine.

# Import required libraries for model evaluation
from sklearn.metrics import mean_squared_error, mean_absolute_percentage_error

Ottimizzare gli iperparametri

SARIMAX tiene conto dei parametri coinvolti nella normale modalità media mobile integrata autoregressiva (ARIMA) (p, d, q), e aggiunge i parametri di stagionalità (P, D, Q, s). Questi argomenti del modello SARIMAX sono denominati rispettivamente ordine (p, d, q) e ordine stagionale (P, D, Q, s). Pertanto, per eseguire il training del modello, è necessario ottimizzare sette parametri.

Parametri di ordine:

  • p: ordine del componente AR, che rappresenta il numero di osservazioni passate nella serie temporale usata per stimare il valore corrente.

    In genere, questo parametro deve essere un numero intero non negativo. I valori comuni sono compresi nell'intervallo da 0 a 3, anche se sono possibili valori più elevati, a seconda delle caratteristiche specifiche dei dati. Un valore superiore p indica una memoria più lunga dei valori passati nel modello.

  • d: l'ordine di differenza, che rappresenta il numero di volte in cui la serie temporale deve essere diversa, per ottenere la stazionarietà.

    Questo parametro deve essere un numero intero non negativo. I valori comuni sono compresi nell'intervallo da 0 a 2. Un valore d di 0 indica che la serie temporale è già stazionaria. I valori più alti indicano il numero di operazioni di differenze necessarie per renderla stazionaria.

  • q: ordine del componente MA, che rappresenta il numero di termini di errore relativi al rumore bianco precedenti utilizzati per stimare il valore corrente.

    Questo parametro deve essere un numero intero non negativo. I valori comuni sono compresi nell'intervallo da 0 a 3, ma per determinate serie temporali potrebbero essere necessari valori più elevati. Un valore q più alto indica una maggiore dipendenza dai termini di errore precedenti per eseguire previsioni.

Parametri di ordine stagionale:

  • P: l'ordine stagionale del componente AR, simile a p ma per la parte stagionale
  • D: l'ordine stagionale di differenze, simile a d ma per la parte stagionale
  • Q: l'ordine stagionale del componente MA, simile a q ma per la parte stagionale
  • s: numero di passaggi temporali per ciclo stagionale (ad esempio, 12 per i dati mensili con stagionalità annuale)
# Hyperparameter tuning
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
print('Examples of parameter combinations for Seasonal ARIMA...')
print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[1]))
print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[2]))
print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[3]))
print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[4]))

SARIMAX ha altri parametri:

  • enforce_stationarity: indica se il modello deve applicare o meno la stazione ai dati delle serie temporali, prima di adattare il modello SARIMAX.

    Se enforce_stationarity è impostato su True (impostazione predefinita), indica che il modello SARIMAX deve applicare la stazionarietà ai dati delle serie temporali. Il modello SARIMAX applica quindi automaticamente differenze ai dati, per renderlo stazionario, come specificato dagli ordini d e D , prima di adattare il modello. Si tratta di una pratica comune perché molti modelli di serie temporali, tra cui SARIMAX, presuppongono che i dati siano stazionari.

    Per una serie temporale non stazionaria (ad esempio che presenta tendenze o stagionalità), è consigliabile impostare enforce_stationarity su Truee lasciare che il modello SARIMAX gestisca la differenza per ottenere la stazionarietà. Per una serie temporale fissa (ad esempio, una senza tendenze o stagionalità), impostare enforce_stationarity su per False evitare differenze non necessarie.

  • enforce_invertibility: controlla se il modello deve applicare o meno l'invertibilità sui parametri stimati durante il processo di ottimizzazione.

    Se enforce_invertibility è impostato su True (impostazione predefinita), indica che il modello SARIMAX deve applicare l'invertibilità ai parametri stimati. L'invertibilità garantisce che il modello sia ben definito e che i coefficienti AR e MA stimati atterrino all'interno dell'intervallo di stazionarietà.

    L'imposizione dell'invertibilità consente di garantire che il modello SARIMAX rispetti i requisiti teorici per un modello di serie temporale stabile. Consente inoltre di evitare problemi con la stima e la stabilità del modello.

L'impostazione predefinita è un modello AR(1). Questo si riferisce a (1, 0, 0). Tuttavia, è prassi comune provare diverse combinazioni dei parametri dell'ordine e dei parametri degli ordini stagionali e valutare le prestazioni del modello per un set di dati. I valori appropriati possono variare da una serie temporale a un'altra.

La determinazione dei valori ottimali comporta spesso l'analisi della funzione di correzione automatica (ACF) e della funzione di correzione automatica parziale (PACF) dei dati delle serie temporali. Spesso comporta anche l'uso dei criteri di selezione del modello, ad esempio il criterio di informazioni Akaike (AIC) o il criterio informativo bayesiano (BIC).

Ottimizzare gli iperparametri:

# Tune the hyperparameters to determine the best model
for param in pdq:
    for param_seasonal in seasonal_pdq:
        try:
            mod = sm.tsa.statespace.SARIMAX(y,
                                            order=param,
                                            seasonal_order=param_seasonal,
                                            enforce_stationarity=False,
                                            enforce_invertibility=False)
            results = mod.fit(disp=False)
            print('ARIMA{}x{}12 - AIC:{}'.format(param, param_seasonal, results.aic))
        except:
            continue

Dopo la valutazione dei risultati precedenti, è possibile determinare i valori sia per i parametri order che per i parametri dell'ordine stagionale. La scelta è order=(0, 1, 1) e seasonal_order=(0, 1, 1, 12), che offrono il valore AIC più basso, ad esempio 279,58. Usare questi valori per eseguire il training del modello.

Eseguire il training del modello

# Model training 
mod = sm.tsa.statespace.SARIMAX(y,
                                order=(0, 1, 1),
                                seasonal_order=(0, 1, 1, 12),
                                enforce_stationarity=False,
                                enforce_invertibility=False)
results = mod.fit(disp=False)
print(results.summary().tables[1])

Questo codice visualizza una previsione delle serie temporali per i dati di vendita di mobili. I risultati tracciati mostrano sia i dati osservati che la previsione un passo avanti, con un'area ombreggiata per l'intervallo di confidenza.

# Plot the forecasting results
pred = results.get_prediction(start=maximim_date, end=maximim_date+pd.DateOffset(months=6), dynamic=False) # Forecast for the next 6 months (months=6)
pred_ci = pred.conf_int() # Extract the confidence intervals for the predictions
ax = y['2019':].plot(label='observed')
pred.predicted_mean.plot(ax=ax, label='One-step ahead forecast', alpha=.7, figsize=(12, 7))
ax.fill_between(pred_ci.index,
                pred_ci.iloc[:, 0],
                pred_ci.iloc[:, 1], color='k', alpha=.2)
ax.set_xlabel('Date')
ax.set_ylabel('Furniture Sales')
plt.legend()
plt.show()

# Validate the forecasted result
predictions = results.get_prediction(start=maximim_date-pd.DateOffset(months=6-1), dynamic=False)
# Forecast on the unseen future data
predictions_future = results.get_prediction(start=maximim_date+ pd.DateOffset(months=1),end=maximim_date+ pd.DateOffset(months=6),dynamic=False)

Usare predictions per valutare le prestazioni del modello, in contrasto con i valori effettivi. Il valore predictions_future indica previsioni future.

# Log the model and parameters
model_name = f"{EXPERIMENT_NAME}-Sarimax"
with mlflow.start_run(run_name="Sarimax") as run:
    mlflow.statsmodels.log_model(results,model_name,registered_model_name=model_name)
    mlflow.log_params({"order":(0,1,1),"seasonal_order":(0, 1, 1, 12),'enforce_stationarity':False,'enforce_invertibility':False})
    model_uri = f"runs:/{run.info.run_id}/{model_name}"
    print("Model saved in run %s" % run.info.run_id)
    print(f"Model URI: {model_uri}")
mlflow.end_run()

# Load the saved model
loaded_model = mlflow.statsmodels.load_model(model_uri)

Passaggio 4: assegnare un punteggio al modello e salvare le previsioni

Integrare i valori effettivi con i valori previsti per creare un report di Power BI. Archiviare questi risultati in una tabella all'interno del lakehouse.

# Data preparation for Power BI visualization
Future = pd.DataFrame(predictions_future.predicted_mean).reset_index()
Future.columns = ['Date','Forecasted_Sales']
Future['Actual_Sales'] = np.NAN
Actual = pd.DataFrame(predictions.predicted_mean).reset_index()
Actual.columns = ['Date','Forecasted_Sales']
y_truth = y['2023-02-01':]
Actual['Actual_Sales'] = y_truth.values
final_data = pd.concat([Actual,Future])
# Calculate the mean absolute percentage error (MAPE) between 'Actual_Sales' and 'Forecasted_Sales' 
final_data['MAPE'] = mean_absolute_percentage_error(Actual['Actual_Sales'], Actual['Forecasted_Sales']) * 100
final_data['Category'] = "Furniture"
final_data[final_data['Actual_Sales'].isnull()]

input_df = y.reset_index()
input_df.rename(columns = {'Order Date':'Date','Sales':'Actual_Sales'}, inplace=True)
input_df['Category'] = 'Furniture'
input_df['MAPE'] = np.NAN
input_df['Forecasted_Sales'] = np.NAN

# Write back the results into the lakehouse
final_data_2 = pd.concat([input_df,final_data[final_data['Actual_Sales'].isnull()]])
table_name = "Demand_Forecast_New_1"
spark.createDataFrame(final_data_2).write.mode("overwrite").format("delta").save(f"Tables/{table_name}")
print(f"Spark DataFrame saved to delta table: {table_name}")

Passaggio 5: visualizzare in Power BI

Il report di Power BI mostra un errore percentuale assoluto medio (MAPE) pari a 16,58. La metrica MAPE definisce l'accuratezza di un metodo di previsione. Rappresenta l'accuratezza delle quantità previste, rispetto alle quantità effettive.

MAPE è una metrica semplice. Un MAPE del 10% rappresenta che la deviazione media tra i valori previsti e i valori effettivi è 10%, indipendentemente dal fatto che la deviazione sia positiva o negativa. Gli standard dei valori MAPE desiderabili variano in tutti i settori.

La linea blu chiaro in questo grafico rappresenta i valori effettivi delle vendite. La linea blu scuro rappresenta i valori delle vendite previste. Il confronto delle vendite effettive e previste rivela che il modello prevede in modo efficace le vendite per la categoria Furniture nei primi sei mesi del 2023.

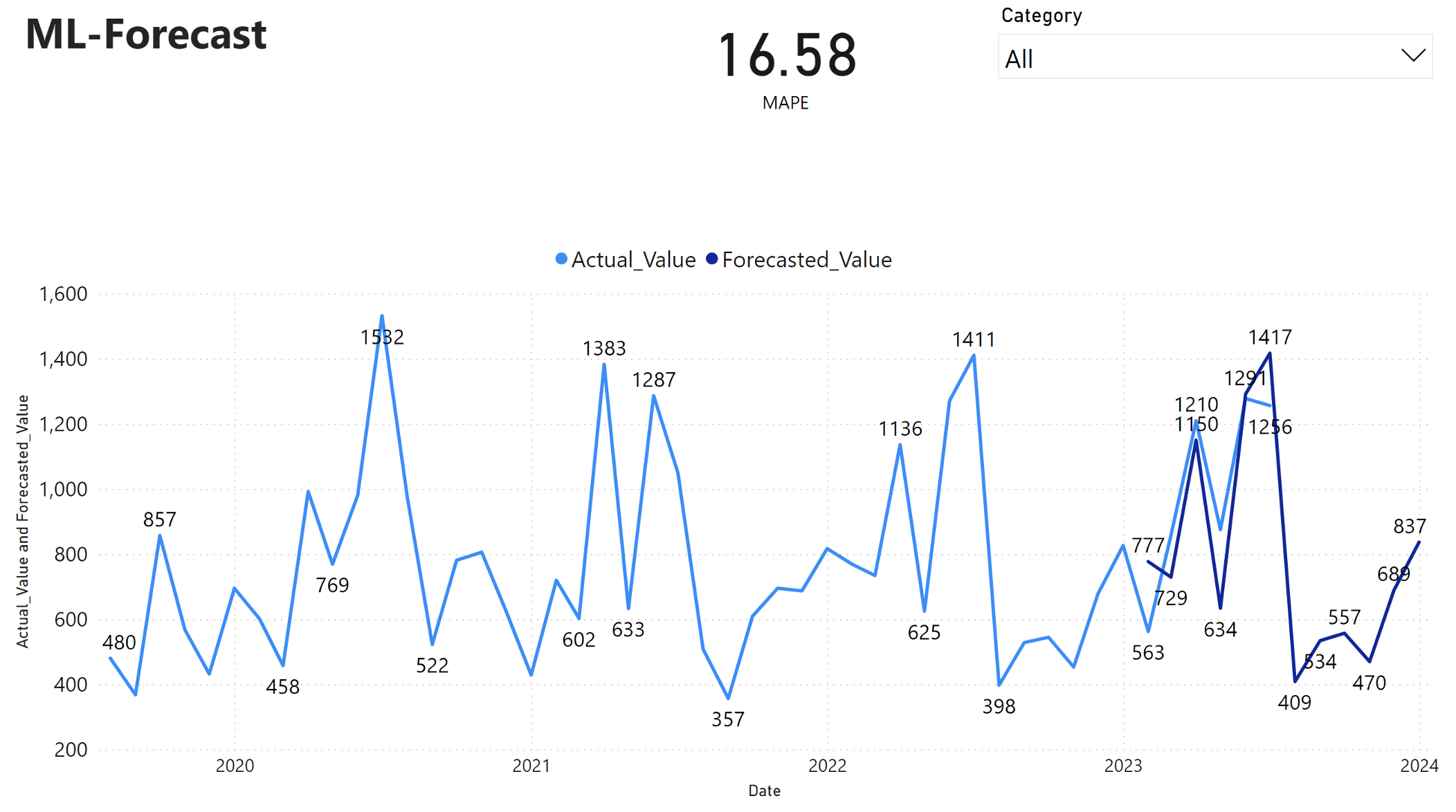
Screenshot di un report di Power BI.

In base a questa osservazione, è possibile avere fiducia nelle capacità di previsione del modello, per le vendite complessive negli ultimi sei mesi del 2023 ed estendendosi nel 2024. Questa fiducia può informare decisioni strategiche sulla gestione dell'inventario, l'approvvigionamento di materie prime e altre considerazioni relative all'azienda.

Contenuto correlato