Vue d’ensemble des géométries

Article
06/13/2023

Cette vue d’ensemble explique comment créer et utiliser des objets ID2D1Geometry pour définir et manipuler des figures 2D. Elle contient les sections suivantes.

Qu’est-ce qu’une géométrie Direct2D ?

Une géométrie Direct2D est un objet ID2D1Geometry . Cet objet peut être une géométrie simple (ID2D1RectangleGeometry, ID2D1RoundedRectangleGeometry ou ID2D1EllipseGeometry), une géométrie de chemin (ID2D1PathGeometry) ou une géométrie composite (ID2D1GeometryGroup et ID2D1TransformedGeometry).

Les géométries Direct2D vous permettent de décrire des figures bidimensionnelles et offrent de nombreuses utilisations, telles que la définition de régions de test d’accès, de régions de clip et même de chemins d’animation.

Les géométries Direct2D sont des ressources immuables et indépendantes de l’appareil créées par ID2D1Factory. En règle générale, vous devez créer des géométries une seule fois et les conserver pendant la durée de vie de l’application, ou jusqu’à ce qu’elles doivent être modifiées. Pour plus d’informations sur les ressources indépendantes de l’appareil et dépendantes de l’appareil, consultez Vue d’ensemble des ressources.

Les sections suivantes décrivent les différents types de géométries.

Géométries simples

Les géométries simples incluent les objets ID2D1RectangleGeometry, ID2D1RoundedRectangleGeometry et ID2D1EllipseGeometry , et peuvent être utilisées pour créer des figures géométriques de base, telles que des rectangles, des rectangles arrondis, des cercles et des ellipses.

Pour créer une géométrie simple, utilisez l’une des méthodes ID2D1Factory::Create<geometryType>Geometry . Ces méthodes créent un objet du type spécifié. Par exemple, pour créer un rectangle, appelez ID2D1Factory::CreateRectangleGeometry, qui retourne un objet ID2D1RectangleGeometry ; pour créer un rectangle arrondi, appelez ID2D1Factory::CreateRoundedRectangleGeometry, qui retourne un objet ID2D1RoundedRectangleGeometry , etc.

L’exemple de code suivant appelle la méthode CreateEllipseGeometry , en passant une structure de points de suspension dont le centre est défini sur (100, 100), le rayon x sur 100 et le rayon y sur 50. Ensuite, il appelle DrawGeometry, en passant la géométrie d’ellipse retournée, un pointeur vers un ID2D1SolidColorBrush noir et une largeur de trait de 5. L’illustration suivante montre la sortie de l’exemple de code.

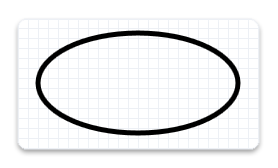
illustration d’une ellipse

ID2D1EllipseGeometry *m_pEllipseGeometry;

if (SUCCEEDED(hr))
{
    hr = m_pD2DFactory->CreateEllipseGeometry(
        D2D1::Ellipse(D2D1::Point2F(100.f, 60.f), 100.f, 50.f),
        &m_pEllipseGeometry
        );
}

m_pRenderTarget->DrawGeometry(m_pEllipseGeometry, m_pBlackBrush, 5);

Pour dessiner le contour d’une géométrie, utilisez la méthode DrawGeometry . Pour peindre son intérieur, utilisez la méthode FillGeometry .

Géométries de chemin d’accès

Les géométries de chemin d’accès sont représentées par l’interface ID2D1PathGeometry . Ces objets peuvent être utilisés pour décrire des figures géométriques complexes composées de segments tels que des arcs, des courbes et des lignes. L’illustration suivante montre un dessin créé à l’aide de la géométrie de chemin d’accès.

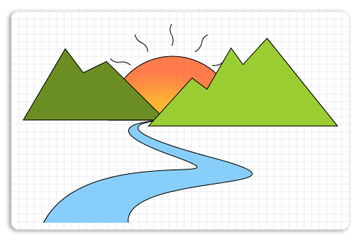
illustration d’une rivière, de montagnes et du soleil

Pour plus d’informations et d’exemples, consultez Vue d’ensemble des géométries de chemin.

Géométries composites

Une géométrie composite est une géométrie groupée ou combinée à un autre objet geometry, ou à une transformation. Les géométries composites incluent les objets ID2D1TransformedGeometry et ID2D1GeometryGroup .

Groupes Geometry

Les groupes Geometry sont un moyen pratique de regrouper plusieurs géométries en même temps afin que toutes les figures de plusieurs géométries distinctes soient concaténées en une seule. Pour créer un objet ID2D1GeometryGroup , appelez la méthode CreateGeometryGroup sur l’objet ID2D1Factory , en passant le fillMode avec les valeurs possibles de D2D1_FILL_MODE_ALTERNATE (alternative) et D2D1_FILL_MODE_WINDING, un tableau d’objets geometry à ajouter au groupe geometry et le nombre d’éléments dans ce tableau.

L’exemple de code suivant déclare d’abord un tableau d’objets geometry. Ces objets sont quatre cercles concentriques qui ont les rayons suivants : 25, 50, 75 et 100. Ensuite, appelez le CreateGeometryGroup sur l’objet ID2D1Factory , en passant D2D1_FILL_MODE_ALTERNATE, un tableau d’objets geometry à ajouter au groupe geometry et le nombre d’éléments dans ce tableau.

ID2D1Geometry *ppGeometries[] =
{
    m_pEllipseGeometry1,
    m_pEllipseGeometry2,
    m_pEllipseGeometry3,
    m_pEllipseGeometry4
};

hr = m_pD2DFactory->CreateGeometryGroup(
    D2D1_FILL_MODE_ALTERNATE,
    ppGeometries,
    ARRAYSIZE(ppGeometries),
    &m_pGeoGroup_AlternateFill
    );

if (SUCCEEDED(hr))
{
    hr = m_pD2DFactory->CreateGeometryGroup(
        D2D1_FILL_MODE_WINDING,
        ppGeometries,
        ARRAYSIZE(ppGeometries),
        &m_pGeoGroup_WindingFill
        );
}

L’illustration suivante montre les résultats du rendu des deux géométries de groupe à partir de l’exemple.

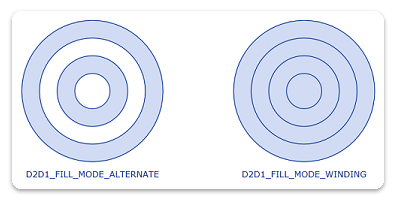
illustration de deux ensembles de quatre cercles concentriques, l’un avec des anneaux alternés remplis et l’autre avec tous les anneaux remplis

Géométries transformées

Il existe plusieurs façons de transformer une géométrie. Vous pouvez utiliser la méthode SetTransform d’une cible de rendu pour transformer tout ce que la cible de rendu dessine, ou vous pouvez associer une transformation directement à une géométrie à l’aide de la méthode CreateTransformedGeometry pour créer une id2D1TransformedGeometry.

La méthode que vous devez utiliser dépend de l’effet souhaité. Lorsque vous utilisez la cible de rendu pour transformer, puis restituer une géométrie, la transformation affecte tout ce qui concerne la géométrie, y compris la largeur de n’importe quel trait que vous avez appliqué. En revanche, lorsque vous utilisez une id2D1TransformedGeometry, la transformation affecte uniquement les coordonnées qui décrivent la forme. La transformation n’affecte pas l’épaisseur du trait lorsque la géométrie est dessinée.

Notes

À compter de Windows 8 la transformation mondiale n’affecte pas l’épaisseur des traits avec D2D1_STROKE_TRANSFORM_TYPE_FIXEDou D2D1_STROKE_TRANSFORM_TYPE_HAIRLINE. Vous devez utiliser ces types de transformation pour obtenir des traits de transformation indépendants

L’exemple suivant crée un ID2D1RectangleGeometry, puis le dessine sans le transformer. Il produit la sortie illustrée dans l’illustration suivante.

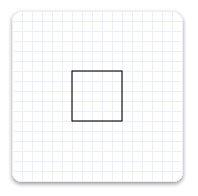
illustration d’un rectangle

hr = m_pD2DFactory->CreateRectangleGeometry(
    D2D1::RectF(150.f, 150.f, 200.f, 200.f),
    &m_pRectangleGeometry
    );

// Draw the untransformed rectangle geometry.
m_pRenderTarget->DrawGeometry(m_pRectangleGeometry, m_pBlackBrush, 1);

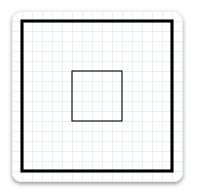
L’exemple suivant utilise la cible de rendu pour mettre à l’échelle la géométrie d’un facteur 3, puis la dessine. L’illustration suivante montre le résultat du dessin du rectangle sans transformation et avec la transformation. Notez que le trait est plus épais après la transformation, même si l’épaisseur du trait est 1.

illustration d’un rectangle plus petit à l’intérieur d’un rectangle plus grand avec un trait plus épais

// Transform the render target, then draw the rectangle geometry again.
m_pRenderTarget->SetTransform(
    D2D1::Matrix3x2F::Scale(
        D2D1::SizeF(3.f, 3.f),
        D2D1::Point2F(175.f, 175.f))
    );

m_pRenderTarget->DrawGeometry(m_pRectangleGeometry, m_pBlackBrush, 1);

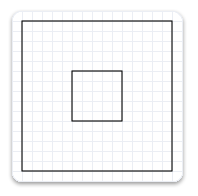
L’exemple suivant utilise la méthode CreateTransformedGeometry pour mettre à l’échelle la géométrie d’un facteur 3, puis la dessiner. Il produit la sortie illustrée dans l’illustration suivante. Notez que, bien que le rectangle soit plus grand, son trait n’a pas augmenté.

illustration d’un rectangle plus petit à l’intérieur d’un rectangle plus grand avec la même épaisseur de trait

 // Create a geometry that is a scaled version
 // of m_pRectangleGeometry.
 // The new geometry is scaled by a factory of 3
 // from the center of the geometry, (35, 35).

 hr = m_pD2DFactory->CreateTransformedGeometry(
     m_pRectangleGeometry,
     D2D1::Matrix3x2F::Scale(
         D2D1::SizeF(3.f, 3.f),
         D2D1::Point2F(175.f, 175.f)),
     &m_pTransformedGeometry
     );

// Replace the previous render target transform.
m_pRenderTarget->SetTransform(D2D1::Matrix3x2F::Identity());

// Draw the transformed geometry.
m_pRenderTarget->DrawGeometry(m_pTransformedGeometry, m_pBlackBrush, 1);

Géométries sous forme de masques

Vous pouvez utiliser un objet ID2D1Geometry comme masque géométrique lorsque vous appelez la méthode PushLayer . Le masque géométrique spécifie la zone du calque qui est composite dans la cible de rendu. Pour plus d’informations, consultez la section Masques géométriques de la vue d’ensemble des couches.

Opérations géométriques

L’interface ID2D1Geometry fournit plusieurs opérations géométriques que vous pouvez utiliser pour manipuler et mesurer des figures géométriques. Par exemple, vous pouvez les utiliser pour calculer et retourner leurs limites, comparer pour voir comment une géométrie est spatialement liée à une autre (utile pour les tests de succès), calculer les zones et les longueurs, et bien plus encore. Le tableau suivant décrit les opérations géométriques courantes.

Opération	Méthode
Combine	CombineWithGeometry
Limites/limites élargies/récupérer des limites, mise à jour de la région sale	Widen, GetBounds, GetWidenedBounds
Test des résultats	FillContainsPoint, StrokeContainsPoint
Trait	StrokeContainsPoint
Comparaison	CompareWithGeometry
Simplification (supprime les arcs et les courbes quadratiques de Bézier)	Simplifier
Pavage	Téssellate
Plan (supprimer l’intersection)	Plan
Calculer la surface ou la longueur d’une géométrie	ComputeArea, ComputeLength, ComputePointAtLength

Notes

À partir de Windows 8, vous pouvez utiliser la méthode ComputePointAndSegmentAtLength sur ID2D1PathGeometry1 pour calculer la surface ou la longueur d’une géométrie.

Combinaison de géométries

Pour combiner une géométrie à une autre, appelez la méthode ID2D1Geometry::CombineWithGeometry . Lorsque vous combinez les géométries, vous spécifiez l’une des quatre façons d’effectuer l’opération de combinaison : D2D1_COMBINE_MODE_UNION (union), D2D1_COMBINE_MODE_INTERSECT (intersection), D2D1_COMBINE_MODE_XOR (xor) et D2D1_COMBINE_MODE_EXCLUDE (exclure). L’exemple de code suivant montre deux cercles qui sont combinés à l’aide du mode de combinaison d’union, où le premier cercle a le point central de (75, 75) et le rayon de 50, et le deuxième cercle a le point central de (125, 75) et le rayon de 50.

HRESULT hr = S_OK;
ID2D1GeometrySink *pGeometrySink = NULL;

// Create the first ellipse geometry to merge.
const D2D1_ELLIPSE circle1 = D2D1::Ellipse(
    D2D1::Point2F(75.0f, 75.0f),
    50.0f,
    50.0f
    );

hr = m_pD2DFactory->CreateEllipseGeometry(
    circle1,
    &m_pCircleGeometry1
    );

if (SUCCEEDED(hr))
{
    // Create the second ellipse geometry to merge.
    const D2D1_ELLIPSE circle2 = D2D1::Ellipse(
        D2D1::Point2F(125.0f, 75.0f),
        50.0f,
        50.0f
        );

    hr = m_pD2DFactory->CreateEllipseGeometry(circle2, &m_pCircleGeometry2);
}


if (SUCCEEDED(hr))
{
    //
    // Use D2D1_COMBINE_MODE_UNION to combine the geometries.
    //
    hr = m_pD2DFactory->CreatePathGeometry(&m_pPathGeometryUnion);

    if (SUCCEEDED(hr))
    {
        hr = m_pPathGeometryUnion->Open(&pGeometrySink);

        if (SUCCEEDED(hr))
        {
            hr = m_pCircleGeometry1->CombineWithGeometry(
                m_pCircleGeometry2,
                D2D1_COMBINE_MODE_UNION,
                NULL,
                NULL,
                pGeometrySink
                );
        }

        if (SUCCEEDED(hr))
        {
            hr = pGeometrySink->Close();
        }

        SafeRelease(&pGeometrySink);
    }
}

L’illustration suivante montre deux cercles combinés à un mode d’union combiné.

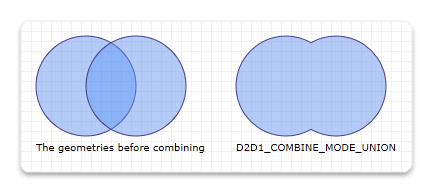
illustration de deux cercles qui se chevauchent combinés en une union

Pour obtenir des illustrations de tous les modes de combinaison, consultez l’énumération D2D1_COMBINE_MODE.

Élargir

La méthode Widen génère une nouvelle géométrie dont le remplissage équivaut à caresser la géométrie existante, puis écrit le résultat dans l’objet ID2D1SimplifiedGeometrySink spécifié. L’exemple de code suivant appelle Open sur l’objet ID2D1PathGeometry . Si Open réussit, il appelle Widen sur l’objet geometry.

ID2D1GeometrySink *pGeometrySink = NULL;
hr = pPathGeometry->Open(&pGeometrySink);
if (SUCCEEDED(hr))
{
    hr = pGeometry->Widen(
            strokeWidth,
            pIStrokeStyle,
            pWorldTransform,
            pGeometrySink
            );

Tessellate

La méthode Tessellate crée un ensemble de triangles enroulés dans le sens des aiguilles d’une montre qui couvrent la géométrie après sa transformation à l’aide de la matrice spécifiée et aplaties à l’aide de la tolérance spécifiée. L’exemple de code suivant utilise Tessellate pour créer une liste de triangles qui représentent pPathGeometry. Les triangles sont stockés dans un id2D1Mesh, pMesh, puis transférés à un membre de classe, m_pStrokeMesh, pour une utilisation ultérieure lors du rendu.

ID2D1Mesh *pMesh = NULL;
hr = m_pRT->CreateMesh(&pMesh);
if (SUCCEEDED(hr))
{
    ID2D1TessellationSink *pSink = NULL;
    hr = pMesh->Open(&pSink);
    if (SUCCEEDED(hr))
    {
        hr = pPathGeometry->Tessellate(
                NULL, // world transform (already handled in Widen)
                pSink
                );
        if (SUCCEEDED(hr))
        {
            hr = pSink->Close();
            if (SUCCEEDED(hr))
            {
                SafeReplace(&m_pStrokeMesh, pMesh);
            }
        }
        pSink->Release();
    }
    pMesh->Release();
}

FillContainsPoint et StrokeContainsPoint

La méthode FillContainsPoint indique si la zone remplie par la géométrie contient le point spécifié. Vous pouvez utiliser cette méthode pour effectuer des tests d’accès. L’exemple de code suivant appelle FillContainsPoint sur un objet ID2D1EllipseGeometry , en passant un point à (0,0) et une matrice d’identité .

BOOL containsPoint1;
hr = m_pCircleGeometry1->FillContainsPoint(
    D2D1::Point2F(0,0),
    D2D1::Matrix3x2F::Identity(),
    &containsPoint1
    );

if (SUCCEEDED(hr))
{
    // Process containsPoint.
}

La méthode StrokeContainsPoint détermine si le trait de la géométrie contient le point spécifié. Vous pouvez utiliser cette méthode pour effectuer des tests d’accès. L’exemple de code suivant utilise StrokeContainsPoint.

BOOL containsPoint;

hr = m_pCircleGeometry1->StrokeContainsPoint(
    D2D1::Point2F(0,0),
    10,     // stroke width
    NULL,   // stroke style
    NULL,   // world transform
    &containsPoint
    );

if (SUCCEEDED(hr))
{
    // Process containsPoint.
}

Simplifier

La méthode Simplifie supprime les arcs et les courbes quadratiques de Bézier d’une géométrie spécifiée. Ainsi, la géométrie résultante contient uniquement des lignes et, éventuellement, des courbes de Bézier cubiques. L’exemple de code suivant utilise Simplifie pour transformer une géométrie avec des courbes de Bézier en une géométrie qui contient uniquement des segments de ligne.

HRESULT D2DFlatten(
    ID2D1Geometry *pGeometry,
    float flatteningTolerance,
    ID2D1Geometry **ppGeometry
    )
{
    HRESULT hr;
    ID2D1Factory *pFactory = NULL;
    pGeometry->GetFactory(&pFactory);

    ID2D1PathGeometry *pPathGeometry = NULL;
    hr = pFactory->CreatePathGeometry(&pPathGeometry);

    if (SUCCEEDED(hr))
    {
        ID2D1GeometrySink *pSink = NULL;
        hr = pPathGeometry->Open(&pSink);

        if (SUCCEEDED(hr))
        {
            hr = pGeometry->Simplify(
                    D2D1_GEOMETRY_SIMPLIFICATION_OPTION_LINES,
                    NULL, // world transform
                    flatteningTolerance,
                    pSink
                    );

            if (SUCCEEDED(hr))
            {
                hr = pSink->Close();

                if (SUCCEEDED(hr))
                {
                    *ppGeometry = pPathGeometry;
                    (*ppGeometry)->AddRef();
                }
            }
            pSink->Release();
        }
        pPathGeometry->Release();
    }

    pFactory->Release();

    return hr;
}

ComputeLength et ComputeArea

La méthode ComputeLength calcule la longueur de la géométrie spécifiée si chaque segment a été roulé dans une ligne. Cela inclut le segment de fermeture implicite si la géométrie est fermée. L’exemple de code suivant utilise ComputeLength pour calculer la longueur d’un cercle spécifié (m_pCircleGeometry1).

float length;

// Compute the area of circle1
hr = m_pCircleGeometry1->ComputeLength(
    D2D1::IdentityMatrix(),
    &length
    );

if (SUCCEEDED(hr))
{
    // Process the length of the geometry.
}

La méthode ComputeArea calcule la zone de la géométrie spécifiée. L’exemple de code suivant utilise ComputeArea pour calculer la zone d’un cercle (m_pCircleGeometry1) spécifié.

float area;

// Compute the area of circle1
hr = m_pCircleGeometry1->ComputeArea(
    D2D1::IdentityMatrix(),
    &area
    );

CompareWithGeometry

La méthode CompareWithGeometry décrit l’intersection entre la géométrie qui appelle cette méthode et la géométrie spécifiée. Les valeurs possibles pour l’intersection incluent D2D1_GEOMETRY_RELATION_DISJOINT (disjoint), D2D1_GEOMETRY_RELATION_IS_CONTAINED (est contenu), D2D1_GEOMETRY_RELATION_CONTAINS (contient) et D2D1_GEOMETRY_RELATION_OVERLAP (chevauchement). « disjoint » signifie que deux remplissages géométriques ne se croisent pas du tout. « est contenu » signifie que la géométrie est entièrement contenue par la géométrie spécifiée. « contains » signifie que la géométrie contient complètement la géométrie spécifiée, et « chevauchement » signifie que les deux géométries se chevauchent, mais ne contient pas complètement l’autre.

L’exemple de code suivant montre comment comparer deux cercles qui ont le même rayon de 50, mais qui sont décalés de 50.

HRESULT hr = S_OK;
ID2D1GeometrySink *pGeometrySink = NULL;

// Create the first ellipse geometry to merge.
const D2D1_ELLIPSE circle1 = D2D1::Ellipse(
    D2D1::Point2F(75.0f, 75.0f),
    50.0f,
    50.0f
    );

hr = m_pD2DFactory->CreateEllipseGeometry(
    circle1,
    &m_pCircleGeometry1
    );

if (SUCCEEDED(hr))
{
    // Create the second ellipse geometry to merge.
    const D2D1_ELLIPSE circle2 = D2D1::Ellipse(
        D2D1::Point2F(125.0f, 75.0f),
        50.0f,
        50.0f
        );

    hr = m_pD2DFactory->CreateEllipseGeometry(circle2, &m_pCircleGeometry2);
}

D2D1_GEOMETRY_RELATION result = D2D1_GEOMETRY_RELATION_UNKNOWN;

// Compare circle1 with circle2
hr = m_pCircleGeometry1->CompareWithGeometry(
    m_pCircleGeometry2,
    D2D1::IdentityMatrix(),
    0.1f,
    &result
    );

if (SUCCEEDED(hr))
{
    static const WCHAR szGeometryRelation[] = L"Two circles overlap.";
    m_pRenderTarget->SetTransform(D2D1::IdentityMatrix());
    if (result == D2D1_GEOMETRY_RELATION_OVERLAP)
    {
        m_pRenderTarget->DrawText(
            szGeometryRelation,
            ARRAYSIZE(szGeometryRelation) - 1,
            m_pTextFormat,
            D2D1::RectF(25.0f, 160.0f, 200.0f, 300.0f),
            m_pTextBrush
            );
    }
}

Plan

La méthode Outline calcule le contour de la géométrie (une version de la géométrie dans laquelle aucune figure ne se croise ou toute autre figure) et écrit le résultat dans un ID2D1SimplifiedGeometrySink. L’exemple de code suivant utilise Outline pour construire une géométrie équivalente sans auto-intersections. Il utilise la tolérance d’aplatissement par défaut.

HRESULT D2DOutline(
    ID2D1Geometry *pGeometry,
    ID2D1Geometry **ppGeometry
    )
{
    HRESULT hr;
    ID2D1Factory *pFactory = NULL;
    pGeometry->GetFactory(&pFactory);

    ID2D1PathGeometry *pPathGeometry = NULL;
    hr = pFactory->CreatePathGeometry(&pPathGeometry);

    if (SUCCEEDED(hr))
    {
        ID2D1GeometrySink *pSink = NULL;
        hr = pPathGeometry->Open(&pSink);

        if (SUCCEEDED(hr))
        {
            hr = pGeometry->Outline(NULL, pSink);

            if (SUCCEEDED(hr))
            {
                hr = pSink->Close();

                if (SUCCEEDED(hr))
                {
                    *ppGeometry = pPathGeometry;
                    (*ppGeometry)->AddRef();
                }
            }
            pSink->Release();
        }
        pPathGeometry->Release();
    }

    pFactory->Release();

    return hr;
}

GetBounds et GetWidenedBounds

La méthode GetBounds récupère les limites de la géométrie. L’exemple de code suivant utilise GetBounds pour récupérer les limites d’un cercle spécifié (m_pCircleGeometry1).

D2D1_RECT_F bounds;

hr = m_pCircleGeometry1->GetBounds(
      D2D1::IdentityMatrix(),
      &bounds
     );

if (SUCCEEDED(hr))
{
    // Retrieve the bounds.
}

La méthode GetWidenedBounds récupère les limites de la géométrie une fois qu’elle a été élargie par la largeur de trait et le style spécifiés, puis transformée par la matrice spécifiée. L’exemple de code suivant utilise GetWidenedBounds pour récupérer les limites d’un cercle (m_pCircleGeometry1) spécifié après avoir été élargi par la largeur de trait spécifiée.

float dashes[] = {1.f, 1.f, 2.f, 3.f, 5.f};

m_pD2DFactory->CreateStrokeStyle(
    D2D1::StrokeStyleProperties(
        D2D1_CAP_STYLE_FLAT,
        D2D1_CAP_STYLE_FLAT,
        D2D1_CAP_STYLE_ROUND,
        D2D1_LINE_JOIN_ROUND,   // lineJoin
        10.f,   //miterLimit
        D2D1_DASH_STYLE_CUSTOM,
        0.f     //dashOffset
        ),
     dashes,
     ARRAYSIZE(dashes)-1,
     &m_pStrokeStyle
     );

D2D1_RECT_F bounds1;
hr = m_pCircleGeometry1->GetWidenedBounds(
      5.0,
      m_pStrokeStyle,
      D2D1::IdentityMatrix(),
      &bounds1
     );
if (SUCCEEDED(hr))
{
    // Retrieve the widened bounds.
}

ComputePointAtLength

La méthode ComputePointAtLength calcule le vecteur de point et de tangente à la distance spécifiée le long de la géométrie. L’exemple de code suivant utilise ComputePointAtLength.

D2D1_POINT_2F point;
D2D1_POINT_2F tangent;

hr = m_pCircleGeometry1->ComputePointAtLength(
    10, 
    NULL, 
    &point, 
    &tangent);

Vue d’ensemble des géométries de chemin
Référence Direct2D

Partager via

Vue d’ensemble des géométries

Qu’est-ce qu’une géométrie Direct2D ?

Géométries simples

Géométries de chemin d’accès

Géométries composites

Groupes Geometry

Géométries transformées

Géométries sous forme de masques

Opérations géométriques

Combinaison de géométries

Élargir

Tessellate

FillContainsPoint et StrokeContainsPoint

Simplifier

ComputeLength et ComputeArea

CompareWithGeometry

Plan

GetBounds et GetWidenedBounds

ComputePointAtLength

Commentaires

Ressources supplémentaires

Partager via

Vue d’ensemble des géométries

Qu’est-ce qu’une géométrie Direct2D ?

Géométries simples

Géométries de chemin d’accès

Géométries composites

Groupes Geometry

Géométries transformées

Géométries sous forme de masques

Opérations géométriques

Combinaison de géométries

Élargir

Tessellate

FillContainsPoint et StrokeContainsPoint

Simplifier

ComputeLength et ComputeArea

CompareWithGeometry

Plan

GetBounds et GetWidenedBounds

ComputePointAtLength

Rubriques connexes

Commentaires

Ressources supplémentaires