Évaluer une fonction de probabilité
Important
Le support de Machine Learning Studio (classique) prend fin le 31 août 2024. Nous vous recommandons de passer à Azure Machine Learning avant cette date.
À partir du 1er décembre 2021, vous ne pourrez plus créer de nouvelles ressources Machine Learning Studio (classique). Jusqu’au 31 août 2024, vous pouvez continuer à utiliser les ressources Machine Learning Studio (classique) existantes.
- Consultez les informations sur le déplacement des projets de machine learning de ML Studio (classique) à Azure Machine Learning.
- En savoir plus sur Azure Machine Learning.
La documentation ML Studio (classique) est en cours de retrait et ne sera probablement plus mise à jour.
Adapte une fonction spécifiée de distribution des probabilités à un jeu de données
Catégorie : Fonctions statistiques
Notes
S’applique à : Machine Learning Studio (classique) uniquement
Des modules par glisser-déposer similaires sont disponibles dans Concepteur Azure Machine Learning.
Vue d’ensemble du module
Cet article explique comment utiliser le module Évaluer la fonction de probabilité dans Machine Learning Studio (classique), pour calculer les mesures statistiques qui décrivent la distribution d’une colonne, comme bernoulli, Pareto ou les distributions Poisson.
Pour utiliser ce modèle, connectez un jeu de données qui contient au moins une colonne de valeurs numériques et choisissez une distribution de probabilité à tester. Le module retourne une table de données qui contient des valeurs de la fonction de probabilité spécifiée.
Vous pouvez calculer l’une de ces valeurs pour la distribution de probabilité choisie :
- fonction de distribution cumulative (cdf)
- fonction de distribution cumulative inverse (InverseCdf)
- fonction de densité de probabilité (Pdf)
Pourquoi la distribution de probabilité est-elle utile ?
Lorsque vous évaluez vos données par rapport à une distribution de probabilité, vous mappez des valeurs de colonne par rapport à un ensemble de valeurs avec des propriétés connues. En sachant si vos données correspondent à l’une de ces distributions connues, vous pouvez déduire d’autres propriétés de vos données. En général, vous pouvez obtenir de meilleures prédictions à partir d'un modèle quand vous pouvez identifier la distribution qui répond le mieux aux données.
La question de la fonction de distribution de probabilité à utiliser dépend à la fois des données et des variables mesurées. Par exemple, certaines distributions sont conçues pour décrire les probabilités de valeurs discrètes; d’autres sont destinées à être utilisées uniquement avec des variables numériques continues. Pour certaines distributions, vous devez également connaître à l’avance une moyenne attendue, des degrés de liberté, etc. Pour plus d’informations, consultez Distributions de probabilités prises en charge
Guide pratique pour configurer la fonction Évaluer la probabilité
Toutes les options changent en fonction du type de distribution de probabilité que vous souhaitez calculer. Si vous modifiez la méthode de distribution de probabilité, d’autres sélections que vous avez peut-être effectuées sont réinitialisées.
Par conséquent, veillez à choisir d’abord l’option Distribution !
Le jeu de données utilisé comme entrée doit contenir des données numériques. D’autres types de données sont ignorés.
Pour chaque analyse, vous pouvez appliquer une méthode de distribution de probabilité unique. Pour calculer une distribution de probabilité différente, ajoutez une instance distincte du module pour chaque distribution que vous envisagez de tester.
Ajoutez le module Évaluer la fonction de probabilité à votre expérience. Vous trouverez ce module dans la catégorie Fonctions statistiques dans Machine Learning Studio (classique).
Connecter un jeu de données qui contient au moins une colonne de nombres.
Utilisez l’option Distribution pour sélectionner le type de distribution de probabilité que vous souhaitez calculer. Consultez les distributions de probabilité prises en charge pour obtenir la liste des options et leurs arguments requis.
Définissez tous les paramètres requis par la distribution.
Choisissez l’une des trois statistiques à créer : la fonction de distribution cumulative (cdf), la fonction de distribution cumulative inverse (InverseCdf) ou la fonction de densité de probabilité (pdf).
Consultez la section Notes techniques pour connaître les définitions.
Utilisez le sélecteur de colonnes pour choisir les colonnes sur lesquelles calculer la distribution de probabilité sélectionnée.
Toutes les colonnes que vous sélectionnez doivent avoir un type de données numérique.
La plage de données dans la colonne doit également être valide compte tenu de la fonction de probabilité sélectionnée. Sinon, une erreur ou un résultat non numérique (Nan) peuvent se produire.
Pour les colonnes fragmentées, les valeurs correspondant à des zéros en arrière-plan ne sont pas traitées.
Utilisez l’option Mode Résultat pour spécifier comment générer les résultats. Vous pouvez remplacer les valeurs de colonne par les valeurs de distribution de probabilité, ajouter les nouvelles valeurs au jeu de données ou renvoyer uniquement les valeurs de distribution de probabilité.
Exécutez l’expérience ou cliquez avec le bouton droit sur le module Évaluer la fonction de probabilité , puis cliquez sur Exécuter sélectionné.
Résultats
Le tableau suivant contient un exemple de résultats, à l’aide de l’option Ajout , sur une colonne de température unique de l’exemple de jeu de données Forest Fires .
| temp | StandardNormal.Cdf(temp) | StandardNormal.Pdf(temp) | FFisher.cdf(temp) | FFisher.cdf(temp) |
|---|---|---|---|---|
| 8,2 | 1 | 1 | 0.984774 | 0.004349 |
| 18 | 1 | 1 | 0.997896 | 0.000311 |
| 14.6 | 1 | 1 | 0.996352 | 0.000648 |
| 8.3 | 1 | 1 | 0.985201 | 0.004187 |
| 11,4 | 1 | 1 | 0.993147 | 0.001502 |
Les en-têtes des colonnes générées contiennent la distribution de probabilité utilisée.
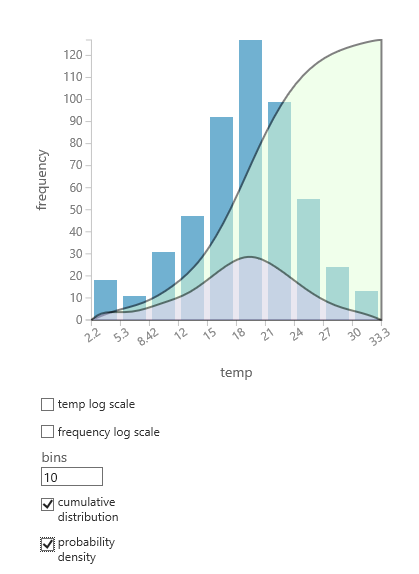
Si vous ne savez pas quelle distribution de probabilité est susceptible de correspondre à vos données, vous pouvez créer un graphique rapide de la distribution cumulative et de la densité de probabilité pour toute colonne numérique.
- Cliquez avec le bouton droit sur le jeu de données ou la sortie du module, puis sélectionnez Visualiser.
- Sélectionnez la colonne d’intérêt et, dans le volet Histogramme , sélectionnez la distribution cumulative ou la densité de probabilité.
- Un graphique de la distribution, comme le suivant, est superposé sur l’histogramme représentant les données.
Distributions de probabilité prises en charge
Le module Évaluer la fonction de probabilité prend en charge les distributions suivantes :
Bernoulli
La distribution Bernoulli est une distribution sur des valeurs binaires : en d’autres termes, elle modélise la distribution attendue lorsque seules deux valeurs sont possibles.
Pour calculer, sélectionnez Bernoulli et définissez les options suivantes :
- Probabilité de réussite
Le paramètre p spécifie la probabilité qu'un 1 soit généré. Tapez une valeur numérique (float) comprise entre 0,0 et 1,0, indiquant la probabilité de réussite. La valeur par défaut est .5.
Bêta
La distribution Bêta est une distribution à variable unique continue.
Pour calculer, sélectionnez Bêta et définissez les options suivantes :
Graphique à base de formes
Tapez une valeur pour modifier la forme de la distribution.Un paramètre de forme est tout paramètre d'une distribution de probabilité qui ne définit pas son emplacement ou son échelle. Par conséquent, quand vous entrez une valeur pour la forme, le paramètre modifie la forme de la distribution au lieu de la déplacer, de l'étirer ou de la réduire.
La valeur doit être numérique (
double). La valeur par défaut est 1.0.Mettre à l'échelle
Tapez une valeur numérique à utiliser pour la mise à l'échelle de la distribution.En appliquant une valeur d'échelle à la distribution, vous pouvez la réduire ou l'étirer.
La valeur par défaut est 1,0. Les valeurs doivent être des valeurs numériques positives.
Limite supérieure
Tapez une valeur numérique (double) représentant la limite supérieure de la distribution. La valeur par défaut est 1.0.Limite inférieure
Tapez une valeur numérique (double) représentant la limite inférieure de la distribution. L’option par défaut est 0.0.
Binomiale
La distribution binomiale est une distribution univariée discrète. La distribution binomiale est utilisée pour modéliser le nombre de réussites dans un échantillon. Un remplacement est utilisé lors de l'échantillonnage. Pour un échantillonnage sans remplacement, utilisez la distribution hypergéométrique.
Pour calculer, sélectionnez Binomial et définissez les options suivantes :
Probabilité de réussite
Tapez une valeur numérique (float) comprise entre 0,0 et 1,0, indiquant la probabilité de réussite. La valeur par défaut est .5.Nombre d'essais
Spécifiez le nombre d'essais.Utilisez un
integer, avec une valeur minimale de 1. La valeur par défaut est 3.
Cauchy
La distribution de Cauchy est une distribution de probabilité continue symétrique.
Pour calculer, sélectionnez Cauchy et définissez les options suivantes :
Lieu
Tapez un nombre (double) qui représente l’emplacement du0e élément.En spécifiant une valeur pour le paramètre Emplacement, vous pouvez décaler la distribution de probabilité vers le haut ou vers le bas d'une échelle numérique.
L’option par défaut est 0.0.
Khi carré
La distribution chi-square est une somme des carrés de k indépendant, standard, normal, variables aléatoires.
Pour calculer, sélectionnez ChiSquare et définissez les options suivantes :
- Nombre de degrés de liberté Tapez un nombre (
double) pour spécifier les degrés de liberté. La valeur par défaut est 1.0.
Distribution Khi carré unilatérale à droite
Cette option fournit une distribution chi-carrée à droite.
Pour calculer, sélectionnez ChiSquareRightTailed et définissez les options suivantes :
- Nombre de degrés de liberté
Tapez une valeur numérique (double) pour indiquer les degrés de liberté. La valeur par défaut est 1.0.
Exponentielle
La distribution exponentielle est une distribution sur les nombres réels paramétrés par un paramètre non négatif.
Pour calculer, sélectionnez Exponentiel et définissez les options suivantes :
- Lambda
Tapez une valeur numérique (double) à utiliser comme paramètre lambda. La valeur par défaut est 1.0.
FFisher
Génère la probabilité de la statistique Fisher pour un échantillon, également connu sous le nom de distribution Fisher F. Cette distribution est bilatérale.
Pour calculer, sélectionnez FFisher et définissez les options suivantes :
Degrés de liberté du numérateur
Tapez une valeur numérique (double) pour spécifier les degrés de liberté utilisés dans le numérateur. La valeur par défaut est 3.0.Degrés de liberté du dénominateur
Tapez une valeur numérique (double) pour spécifier les degrés de liberté utilisés dans le dénominateur. La valeur par défaut est 6.0.
Distribution FFisher unilatérale à droite
Crée une distribution de Fisher à droite. La distribution de Fisher est également appelée distribution de Fisher F, distribution de Snedecor ou distribution de Fisher-Snedecor. Cette forme particulière de la distribution est unilatérale à droite.
Pour calculer, sélectionnez FFisherRightTailed et définissez les options suivantes :
Degrés de liberté du numérateur
Tapez une valeur numérique (double) pour spécifier les degrés de liberté utilisés dans le numérateur. La valeur par défaut est 3.0.Degrés de liberté du dénominateur
Tapez une valeur numérique (double) pour spécifier les degrés de liberté utilisés dans le dénominateur. La valeur par défaut est 6.0.
Gamma
La distribution Gamma est une famille de distributions de probabilités continues avec deux paramètres. Par exemple, la distribution Khi carré est un cas particulier de la distribution Gamma.
Pour calculer, sélectionnez Gamma et définissez les options suivantes :
Mettre à l'échelle
Tapez une valeur numérique à utiliser pour la mise à l'échelle de la distribution.En appliquant une valeur d'échelle à la distribution, vous pouvez la réduire ou l'étirer.
La valeur par défaut est 1,0. Les valeurs doivent être des valeurs numériques positives.
Lieu
Tapez un nombre (double) qui représente l’emplacement du0e élément.En spécifiant une valeur pour le paramètre Emplacement, vous pouvez décaler la distribution de probabilité vers le haut ou vers le bas d'une échelle numérique.
L’option par défaut est 0.0.
Loi d'extremum généralisée
Crée une distribution développée pour gérer des valeurs extrêmes. La loi d'extremum généralisée (GEV, Generalized Extreme Value) est un groupe de distributions de probabilités continues qui combine les distributions de Gumbel, de Fréchet et de Weibull (également appelées distributions de valeurs extrêmes de type I, II et III).
Pour plus d’informations sur la théorie des valeurs extrêmes, consultez cet article dans Wikipédia: Fisher-Tippet-Gnedenko théorème.
Pour calculer, sélectionnez GeneralizedExtremeValues et définissez les options suivantes :
Graphique à base de formes
Tapez une valeur pour modifier la forme de la distribution.Un paramètre de forme est tout paramètre d'une distribution de probabilité qui ne définit pas son emplacement ou son échelle. Par conséquent, quand vous entrez une valeur pour la forme, le paramètre modifie la forme de la distribution au lieu de la déplacer, de l'étirer ou de la réduire.
La valeur doit être numérique (
double). La valeur par défaut est 1.0.Mettre à l'échelle
Tapez une valeur numérique à utiliser pour la mise à l'échelle de la distribution.En appliquant une valeur d'échelle à la distribution, vous pouvez la réduire ou l'étirer.
La valeur par défaut est 1,0. Les valeurs doivent être des valeurs numériques positives.
Lieu
Tapez un nombre (double) qui représente l’emplacement du0e élément.En tapant une valeur pour le paramètre Emplacement, vous pouvez décaler la distribution de probabilité vers le haut ou vers le bas d'une échelle numérique.
L’option par défaut est 0.0.
Géométrique
La distribution géométrique est une distribution sur des entiers positifs paramétrés par un nombre réel positif.
Pour calculer, sélectionnez Géométrique et définissez les options suivantes :
- Probabilité de réussite
Tapez une valeur numérique (float) comprise entre 0,0 et 1,0, indiquant la probabilité de réussite. La valeur par défaut est .5.
Notes
Cette implémentation de la distribution géométrique ne génère pas de zéros.
GumbelMax
La distribution de Gumbel est l'une des distributions de valeurs extrêmes. L'option GumbelMax implémente la distribution de valeurs extrêmes de type 1 maximum.
Pour calculer, sélectionnez GumbelMax et définissez les options suivantes :
Mettre à l'échelle
Tapez une valeur numérique à utiliser pour la mise à l'échelle de la distribution.En appliquant une valeur d'échelle à la distribution, vous pouvez la réduire ou l'étirer.
La valeur par défaut est 1,0. Les valeurs doivent être des valeurs numériques positives.
Lieu
Tapez un nombre (double) qui représente l’emplacement du0e élément.En tapant une valeur pour le paramètre Emplacement, vous pouvez décaler la distribution de probabilité vers le haut ou vers le bas d'une échelle numérique.
L’option par défaut est 0.0.
GumbelMin
La distribution de Gumbel est l'une des distributions de valeurs extrêmes. La distribution de Gumbel est également désignée sous le nom de distribution de valeurs extrêmes minimum ou distribution de valeurs extrêmes de type I minimum. L’option GumbelMin implémente la distribution Minimum Extreme Value Type 1.
Pour calculer, sélectionnez GumbelMin et devez définir les options suivantes :
Mettre à l'échelle
Tapez une valeur numérique à utiliser pour la mise à l'échelle de la distribution.En appliquant une valeur d'échelle à la distribution, vous pouvez la réduire ou l'étirer.
La valeur par défaut est 1,0. Les valeurs doivent être des valeurs numériques positives.
Lieu
Tapez un nombre (double) qui représente l’emplacement du0e élément.En tapant une valeur pour le paramètre Emplacement, vous pouvez décaler la distribution de probabilité vers le haut ou vers le bas d'une échelle numérique.
L’option par défaut est 0.0.
Hypergéométrique
La distribution hypergéométrique est une distribution de probabilité discrète qui décrit le nombre de réussites dans une séquence de n dessine d’une population finie sans remplacement, tout comme la distribution binomiale décrit le nombre de réussites pour les dessins avec remplacement.
Pour calculer, sélectionnez Hypergeometric et définissez les options suivantes :
Nombre d’exemples
Tapez un entier qui indique le nombre d'échantillons à utiliser. La valeur par défaut est 9.Nombre de réussites
Tapez un entier indiquant la valeur de réussite. La valeur par défaut est 24.Taille de la population
Spécifiez la taille de la population à utiliser lors de l'estimation de la distribution hypergéométrique.
Laplace
La distribution Laplace est une distribution sur les nombres réels paramétrés par une moyenne et par un paramètre d’échelle.
Pour calculer, sélectionnez Laplace distribution et définissez les options suivantes :
Mettre à l'échelle
Tapez une valeur numérique à utiliser pour la mise à l'échelle de la distribution.En appliquant une valeur d'échelle à la distribution, vous pouvez la réduire ou l'étirer.
La valeur par défaut est 1,0. Les valeurs doivent être des valeurs numériques positives.
Lieu
Tapez un nombre (double) qui représente l’emplacement du0e élément.En tapant une valeur pour le paramètre Emplacement, vous pouvez décaler la distribution de probabilité vers le haut ou vers le bas d'une échelle numérique.
L’option par défaut est 0.0.
Logistique
La distribution logistique est similaire à la distribution normale, mais n'a aucune limite du côté gauche. La distribution logistique est utilisée dans les modèles de réseau neuronal et de régression logistique ainsi que pour la modélisation de données de sciences de la vie.
Pour calculer, sélectionnez Logistique et définissez les options suivantes :
Mettre à l'échelle
Tapez une valeur numérique à utiliser pour la mise à l'échelle de la distribution.En appliquant une valeur d'échelle à la distribution, vous pouvez la réduire ou l'étirer.
La valeur par défaut est 1,0. Les valeurs doivent être des valeurs numériques positives.
Mean
Tapez une valeur numérique (double) indiquant la valeur moyenne estimée de la distribution. L’option par défaut est 0.0.
Lognormale
La distribution Lognormal est une distribution à variable unique continue.
Pour calculer, sélectionnez Lognormal et définissez les options suivantes :
Mean
Tapez un nombre (double) qui indique la valeur moyenne estimée de la distribution. L’option par défaut est 0.0.Écart
Tapez une valeur numérique (double) positive indiquant l'écart type estimé de la distribution. La valeur par défaut est 1.0.
Binomiale négative
La distribution binomiale négative est une distribution sur les nombres naturel avec deux paramètres (r, p). Dans le cas particulier qui r est un entier, vous pouvez interpréter la distribution comme le nombre de queues avant la tête rth lorsque la probabilité de la tête est p.
Pour calculer, sélectionnez NegativeBinomial et définissez les options suivantes :
Probabilité de réussite
Tapez une valeur numérique (float) comprise entre 0,0 et 1,0, indiquant la probabilité de réussite. La valeur par défaut est .5.Nombre de réussites
Tapez un entier indiquant la valeur de réussite. La valeur par défaut est 24.
Normal
La distribution normale est également connue sous le nom de distribution gaussienne.
Pour calculer, sélectionnez Normal et définissez les options suivantes :
Mean
Tapez un nombre (double) qui indique la valeur moyenne estimée de la distribution. L’option par défaut est 0.0.Écart
Tapez une valeur numérique (double) positive indiquant l'écart type estimé de la distribution. La valeur par défaut est 1.0.
Pareto
La distribution de Pareto est une distribution de probabilité de loi de puissance qui a des applications dans les domaines social, scientifique, géophysique et actuariel, ainsi qu'à de nombreux autres types de phénomènes observables.
Pour calculer, sélectionnez Pareto et définissez les options suivantes :
Graphique à base de formes
Tapez une valeur (facultative) pour modifier la forme de la distribution.Un paramètre de forme est tout paramètre d'une distribution de probabilité qui ne définit pas son emplacement ou son échelle. Par conséquent, quand vous entrez une valeur pour la forme, le paramètre modifie la forme de la distribution au lieu de la déplacer, de l'étirer ou de la réduire.
La valeur doit être numérique (
double). La valeur par défaut est 1.0.Mettre à l'échelle
Tapez une valeur (facultative) pour modifier l’échelle de la distribution. En appliquant une valeur d'échelle à la distribution, vous pouvez la réduire ou l'étirer.La valeur doit être numérique (
double). La valeur par défaut est 1.0.
Poisson
Dans cette implémentation, la méthode de Knuth permet de générer des variables aléatoires distribuées selon la loi de Poisson. Pour plus d’informations sur la distribution de Poisson, consultez Régression de Poisson.
Pour calculer, sélectionnez Poisson et définissez les options suivantes :
- Mean
Tapez un nombre (double) qui indique la valeur moyenne estimée de la distribution. L’option par défaut est 0.0.
Rayleigh
La distribution de Rayleigh est une distribution de probabilité continue. Pour illustrer comment elle se présente, la vitesse du vent aura une distribution de Rayleigh si les composants du vecteur de vitesse du vent à deux dimensions sont non corrélés et distribués normalement avec une variance égale.
Pour calculer, sélectionnez Rayleigh et définissez les options suivantes :
- Limite inférieure
Tapez une valeur numérique (double) représentant la limite inférieure de la distribution. L’option par défaut est 0.0.
Normale standard
Cette option fournit la distribution normale standard, sans aucun autre paramètre.
Pour calculer, sélectionnez StandardNormal, puis sélectionnez les colonnes.
t de Student
Cette option implémente la distribution t de Student univariée.
Pour calculer, sélectionnez TStudent et définissez les options suivantes :
- Nombre de degrés de liberté
Tapez une valeur numérique (double) pour indiquer les degrés de liberté. La valeur par défaut est 1.0.
Distribution t de Student unilatérale à droite
Implémente la distribution t de Student à variable unique avec une queue à droite.
Pour calculer, sélectionnez TStudentRightTailed et définissez les options suivantes :
- Nombre de degrés de liberté
Tapez une valeur numérique (double) pour indiquer les degrés de liberté. La valeur par défaut est 1.0.
Distribution t de Student bilatérale
Implémente une distribution t de Student bilatérale.
Pour calculer, sélectionnez TStudentTwoTailed et définissez les options suivantes :
- Nombre de degrés de liberté
Tapez une valeur numérique (double) pour indiquer les degrés de liberté. La valeur par défaut est 1.0.
Uniforme
La distribution uniforme est également appelée distribution rectangulaire.
Pour calculer, sélectionnez Uniform et définissez les options suivantes :
Limite inférieure
Tapez une valeur numérique (double) représentant la limite inférieure de la distribution. L’option par défaut est 0.0.Limite supérieure
Tapez une valeur numérique (double) représentant la limite supérieure de la distribution. La valeur par défaut est 1.0.
Weibull
La distribution de Weibull est largement utilisée en ingénierie de fiabilité. Vous pouvez utiliser son paramètre Shape pour modéliser de nombreuses autres distributions.
Pour calculer, sélectionnez Weibull et définissez les options suivantes :
Graphique à base de formes
Tapez une valeur (facultative) pour modifier la forme de la distribution.Un paramètre de forme est tout paramètre d'une distribution de probabilité qui ne définit pas son emplacement ou son échelle. Par conséquent, quand vous entrez une valeur pour la forme, le paramètre modifie la forme de la distribution au lieu de la déplacer, de l'étirer ou de la réduire.
La valeur doit être numérique (
double). La valeur par défaut est 1.0.Mettre à l'échelle
Tapez une valeur (facultative) pour modifier l’échelle de la distribution. En appliquant une valeur d'échelle à la distribution, vous pouvez la réduire ou l'étirer.La valeur doit être numérique (
double). La valeur par défaut est 1.0.
Notes techniques
Cette section contient des détails, des conseils et des réponses aux questions fréquentes concernant l’implémentation.
Informations d’implémentation
Ce module prend en charge toutes les distributions fournies dans la bibliothèque de valeurs numériques MATH.NET open source. Pour plus d’informations, consultez la documentation de la bibliothèque Math.Net.Numerics.Distribution .
Les distributions à droite et à deux extrémités apparaissent comme des distributions distinctes, et non comme des versions paramétrables des distributions de base. Le comportement actuel consiste à préserver la compatibilité avec Excel.
Définitions
Ce module prend en charge le calcul de l’une de ces valeurs pour la distribution spécifiée :
cdf, ou la fonction de distribution cumulative
Retourne la probabilité d’un événement composé, définie comme la somme des ocurrences lorsque la variable aléatoire prend une valeur inférieure à une valeur x spécifique.
En d’autres termes, il répond à la question : « Quelle est la fréquence des échantillons inférieurs ou égaux à cette valeur ? »
Cette fonction peut être utilisée avec des variables numériques continues et discrètes.
InverseCdf ou la fonction de distribution cumulative inverse
Retourne la valeur associée à une valeur de probabilité cumulative spécifique (cdf).
En d’autres termes, il répond à la question : « Quelle est la valeur de x à laquelle la fonction cdf retourne la probabilité cumulative y ? »
pdf ou la fonction de densité de probabilité
Décrit la probabilité relative pour une variable aléatoire d’être une valeur spécifique.
En d’autres termes, il répond à la question : « Comment les échantillons sont-ils courants exactement à cette valeur ? »
Entrées attendues
| Nom | Type | Description |
|---|---|---|
| Dataset | Table de données | Jeu de données d'entrée |
Paramètres du module
| Nom | Plage | Type | Default | Description |
|---|---|---|---|---|
| Distribution | Quelconque | ProbabilityDistribution | Normale standard | Sélectionnez le type de distribution de probabilité à générer. |
| Méthode | Quelconque | ProbabilityDistributionMethod | Cdf | Sélectionnez la méthode à utiliser lors du calcul de la distribution de probabilité sélectionnée. Les options sont la fonction de distribution cumulée (cdf), la fonction de distribution cumulée inverse (InverseCdf) et la fonction de densité de probabilité ou fonction de masse (pdf). |
| Méthode de distribution binomiale négative | Quelconque | ProbabilityDistributionMethodForNegativeBinomial | Cdf | Si vous sélectionnez la distribution binomiale négative, spécifiez la méthode utilisée pour évaluer la distribution. |
| Probabilité de réussite | [0.0;1.0] | Float | 0.5 | Tapez une valeur à utiliser comme probabilité de réussite. |
| Graphique à base de formes | Quelconque | Float | 1.0 | Tapez une valeur qui modifie la forme de la distribution. |
| Scale | >=0,0 | Float | 1.0 | Tapez une valeur qui modifie l'échelle de la distribution, pour réduire ou étirer sa taille. |
| Nombre d'essais | >=1 | Integer | 3 | Spécifiez le nombre d'essais. |
| Limite inférieure | Quelconque | Float | 0,0 | Tapez un nombre à utiliser comme limite inférieure de la distribution. |
| Limite supérieure | Quelconque | Float | 1.0 | Tapez un nombre à utiliser comme limite supérieure de la distribution. |
| Emplacement | Quelconque | Float | 0,0 | Tapez l'emplacement de l'élément zéro dans la distribution. |
| Nombre de degrés de liberté | Quelconque | Float | 1.0 | Spécifiez le nombre de degrés de liberté. |
| Degrés de liberté du numérateur | Quelconque | Float | 3.0 | Spécifiez le nombre de degrés de liberté du numérateur. |
| Degrés de liberté du dénominateur | Quelconque | Float | 6.0 | Spécifiez le nombre de degrés de liberté du dénominateur. |
| Lambda | >=0,0 | Float | 1.0 | Spécifiez une valeur pour le paramètre Lambda. |
| Nombre d'échantillons | Quelconque | Integer | 9 | Spécifiez le nombre d'échantillons. |
| Nombre de réussites | Quelconque | Integer | 24 | Tapez une valeur à utiliser comme nombre de réussites. |
| Taille de la population | Quelconque | Integer | 52 | Spécifiez la taille de la population. |
| Moyenne | Quelconque | Float | 0,0 | Tapez la valeur moyenne estimée. |
| Écart standard | >=0,0 | Float | 1.0 | Tapez l'écart type estimé. |
| Jeu de colonnes | Quelconque | ColumnSelection | Choisissez les colonnes sur lesquelles calculer la distribution de probabilité. | |
| Mode de résultat | Quelconque | OutputTo | ResultOnly | Spécifiez la façon dont les résultats doivent être enregistrés dans le jeu de données de sortie. Les options sont d'ajouter de nouvelles colonnes, de remplacer les colonnes existantes ou de générer uniquement les résultats. |
Output
| Nom | Type | Description |
|---|---|---|
| Jeu de données de résultats | Table de données | Jeu de données de sortie |
Exception
Pour obtenir la liste complète des messages d’erreur, consultez Codes d’erreur du module.
| Exception | Description |
|---|---|
| Erreur 0017 | Une exception se produit si une ou plusieurs colonnes spécifiées sont d'un type non pris en charge par le module actuel. |
Pour obtenir la liste des erreurs spécifiques aux modules Studio (classique), consultez Machine Learning codes d’erreur.
Pour obtenir la liste des exceptions d’API, consultez Machine Learning codes d’erreur de l’API REST.