Le qubit en informatique quantique
Tout comme les bits sont l’objet d’information fondamental en informatique classique, les qubits (bits quantiques) sont l’objet d’information fondamental en informatique quantique. Pour vous permettre de comprendre cette correspondance, cet article aborde l’exemple le plus simple : un qubit unique.
Représentation d’un qubit
Si un bit, ou chiffre binaire, peut avoir la valeur $0$ ou $1$, un qubit, peut avoir la valeur $0$, $1$ ou une superposition quantique de $0$ et $1$.
L’état d’un qubit unique peut être décrit par un vecteur colonne à deux dimensions de norme unitaire, c’est-à-dire que la somme des carrés des amplitudes de ses entrées doit être égale à $1$. Ce vecteur, appelé vecteur d’état quantique, contient toutes les informations nécessaires pour décrire le système quantique à un qubit tout comme un bit unique contient toutes les informations nécessaires pour décrire l’état d’une variable binaire. Pour connaître les principes de base des vecteurs et des matrices dans l’informatique quantique, consultez Vector et matrices.
Tout vecteur colonne à deux dimensions de nombres réels ou complexes de norme $1$ représente un état quantique possible contenu par un qubit. Ainsi, $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ représente l’état d’un qubit si $\alpha$ et $\beta$ sont des nombres complexes satisfaisant $|\alpha|^2 + |\beta|^2 = 1$. Voici quelques exemples de vecteurs d’état quantique valides représentant des qubits :
$$\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \end{bmatrix}, \begin{bmatrix}\frac{{1}{\sqrt{2}}\\\frac{{1}{\sqrt{2}}\end{bmatrix}, \begin{bmatrix}\frac{1}{\sqrt{{2}}\\\frac{{-1}{\sqrt{2}}\end{bmatrix}, \text{ et }\begin{bmatrix}\frac{1}{\sqrt{{2}}\\\frac{i}{\sqrt{2}}\end{bmatrix}.$$
Les vecteurs d’état quantique $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ et $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ jouent un rôle spécial. Ces deux vecteurs forment une base pour l’espace vectoriel qui décrit l’état du qubit. Ceci signifie que tout vecteur d’état quantique peut être écrit comme somme de ces vecteurs de base. Plus précisément, le vecteur $\begin{bmatrix} x \\ y \end{bmatrix}$ peut être écrit sous la forme $x \begin{bmatrix} 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Alors qu’une rotation de ces vecteurs offrirait une base parfaitement valide pour le qubit, nous choisissons celle-ci en particulier et l’appelons base de calcul.
Nous prenons ces deux états quantiques pour correspondre avec les deux états d’un bit classique, à savoir $0$ et $1$. La convention standard consiste à choisir
$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \qquad 1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix},$$
même si le choix opposé pourrait également être retenu. Ainsi, sur l’infinité de vecteurs d’état quantique à un qubit possibles, seuls deux correspondent aux états des bits classiques. Ce n’est pas le cas de tous les autres états quantiques.
Mesure d’un qubit
Sachant désormais comment représenter un qubit, nous pouvons déterminer intuitivement ce que ces états représentent en abordant le concept de mesure. Une mesure correspond à l’idée informelle d’« observation » du qubit, ce qui ramène immédiatement l’état quantique à l’un des deux états classiques $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ ou $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Quand un qubit donné par le vecteur d’état quantique $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ est mesuré, nous obtenons le résultat $0$ avec la probabilité $|\alpha|^2$ et le résultat $1$ avec la probabilité $|\beta|^2$. Si le résultat est $0$, le nouvel état du qubit est $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ ; si le résultat est $1$, son état est $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Notez que la somme de ces probabilités est égale à $1$ en raison de la condition de normalisation $|\alpha|^2 + |\beta|^2 = 1$.
Les propriétés de mesure signifient également que le signe global du vecteur d’état quantique n’a pas d’importance. Rendre un vecteur négatif équivaut à $\alpha\rightarrow -\alpha$ et $\beta\rightarrow -\beta$. Comme la probabilité de mesure de $0$ et $1$ dépend du carré des amplitudes des termes, l’insertion de ces signes ne change en rien les probabilités. Ces phases sont généralement appelées &« phases globales& » et, plus généralement, peuvent être de forme $e^{i \phi}$ plutôt que simplement $\pm 1$.
Une dernière propriété importante de la mesure est qu’elle ne détruit pas nécessairement tous les vecteurs d’état quantique. Si nous commençons par un qubit dans l’état $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ correspondant à l’état classique $0$, la mesure de cet état produira toujours le résultat $0$ et laissera l’état quantique inchangé. Dans ce sens, s’il y a uniquement des bits classiques (par exemple, des qubits qui sont $\begin{bmatrix}1 \\ 0 \end{bmatrix}$ ou $\begin{bmatrix}0 \\ 1 \end{bmatrix}$), la mesure n’endommage pas le système. Ceci signifie que nous pouvons répliquer des données classiques et les manipuler sur un ordinateur quantique comme on pourrait le faire avec un ordinateur classique. Toutefois, la capacité à stocker des informations dans les deux états à la fois est ce qui élève l’informatique quantique au-delà de ce que permet l’approche classique et empêche les ordinateurs quantiques de copier des données quantiques de manière non discriminatoire. Consultez également cette page sur le théorème de non-clonage.
Visualisation des qubits et transformations à l’aide de la sphère Bloch
Les qubits peuvent également être représentés en $3$D à l’aide de la sphère de Bloch. La sphère de Bloch offre un moyen de décrire un état quantique à un qubit (un vecteur à deux dimensions complexe) sous la forme d’un vecteur à valeurs réelles en trois dimensions. Cet aspect est important parce que nous pouvons alors visualiser les états à un qubit et ainsi de développer un raisonnement précieux pour comprendre les états multiqubits (dont la représentation ne fonctionne malheureusement pas avec la sphère de Bloch). La sphère de Bloch peut être représentée comme suit :
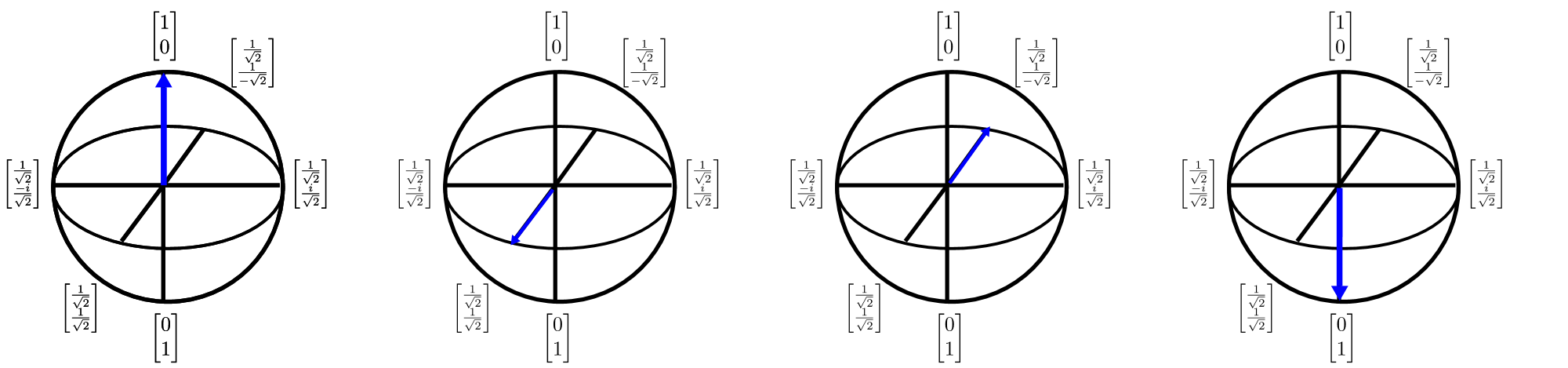
Les flèches de ce schéma indiquent la direction du vecteur d’état quantique et chaque transformation de la flèche peut être considérée comme une rotation autour de l’un des axes cardinaux. Envisager un calcul quantique comme séquence de rotations permet un excellent raisonnement intuitif, qu’il est cependant difficile d’utiliser pour concevoir et décrire des algorithmes. Q# atténue ce problème en fournissant un langage qui permet de décrire ces rotations.
Opérations à un qubit
Les ordinateurs quantiques traitent les données en appliquant un ensemble universel de portes quantiques qui peuvent émuler n’importe quelle rotation du vecteur d’état quantique. Cette notion d’universalité est comparable à celle de l’informatique classique où un ensemble de portes est considéré comme universel si chaque transformation des bits d’entrée peut être effectuée à l’aide d’un circuit de longueur finie. En informatique quantique, les transformations valides que nous sommes autorisés à effectuer sur un qubit sont les transformations unitaires et la mesure. L’opération adjointe, ou transposée conjuguée complexe, revêt une importance capitale en informatique quantique, car elle est nécessaire à l’inversion des transformations quantiques.
Les opérations à qubit unique ou les portes quantiques à qubit unique peuvent être classées en deux catégories : les portes Clifford et les portes non-Clifford. Les portes non-Clifford se composent uniquement de $la porte T$ (également appelée $porte \pi/8$ ).
$$T=\begin{bmatrix} 1 amp ; 0 \\ 0 & ; e^{i\pi/4}\end{bmatrix}.& $$
L’ensemble standard de portes à qubit Clifford, inclus par défaut dans Q#, include
$$H=\frac{{2}}\begin{bmatrix}{1}{\sqrt{ 1 & ; 1 \\ & ;-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & ; 0 0 \\ & ; i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & ; 1 1 \\& ; 0 \end{bmatrix}= HT^4H,$$
$$ Y =\begin{bmatrix} 0 & ; -i \\ amp & ; 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1& ; 0\\ 0& ;-1 \end{bmatrix}=T^4. $$
Ici, les opérations $X$, $Y$ et $Z$ sont utilisées particulièrement fréquemment et sont appelées opérateurs de Pauli, du nom de leur créateur Wolfgang Pauli. Avec la porte non Clifford (porte $T$), ces opérations peuvent être composées pour approximer toute transformation unitaire sur un qubit unique.
Si la précédente représente les portes primitives les plus populaires pour décrire les opérations au niveau logique de la pile (considérez le niveau logique comme le niveau de l’algorithme quantique), il est souvent pratique de considérer les opérations moins basiques au niveau algorithmique, par exemple les opérations plus proches d’un niveau descriptif des fonctions. Heureusement, Q# offre également des méthodes permettant d’implémenter des unitaires de plus haut niveau qui, à leur tour, permettent d’implémenter des algorithmes de haut niveau sans décomposer explicitement tous les éléments en portes Clifford et $T$.
La rotation à un qubit représente la primitive de ce type la plus simple. On considère généralement trois rotations à un qubit comme : $R_x$, $R_y$ et $R_z$. Pour visualiser l’action de la rotation $R_x(\theta)$, par exemple, imaginez que vous pointez votre pouce droit dans la direction de l’axe $x$ de la sphère de Bloch et que vous faites pivoter le vecteur avec votre main sur un angle de $\theta/2$ radians. Ce facteur de confusion de $2$ est dû à la séparation des vecteurs orthogonaux avec un angle de $180^\circ$ quand ils sont tracés sur la sphère de Bloch, mais de $90^\circ$ géométriquement. Les matrices unitaires correspondantes sont les suivantes :
\begin{aligner*}& ; R_z(\theta) = e^{-i\theta Z/2}=\begin{bmatrix} e^{-i\theta/2}& ; 0\\ 0& ; e^{i\theta/2\end{bmatrix}}, \\& ; R_x(\theta) e^{-i\theta X/2=} HR_z(\theta)H =\begin{bmatrix} \cos(\theta/2) & ; -i\sin(\theta/2)\\ -i\sin(\theta/2) & ; \cos(\theta/2) \end{bmatrix}, \\& ; = R_y(\theta) e^-i\theta Y/2=} SHR_z(\theta)HS^\begin{bmatrix}=\dagger \cos(\theta/2) & ; -\sin(\theta/2)\\ \sin(\theta/2) & ; \cos(\theta/2) \end{bmatrix}.{= \end{align*}
Tout comme trois rotations quelconques peuvent être combinées pour effectuer une rotation arbitraire dans trois dimensions, la représentation sur la sphère de Bloch montre que toute matrice unitaire peut également être écrite sous la forme d’une séquence de trois rotations. Plus précisément, pour chaque matrice unitaire $U$, il existe $\alpha,\beta,\gamma,\delta$, de sorte que $U= e^{i\alpha} R_x(\beta)R_z(\gamma)R_x(\delta)$. Ainsi, $R_z(\theta)$ et $H$ forment également un ensemble de portes universel bien qu’il ne s’agisse pas d’un ensemble discret, car $\theta$ peut prendre n’importe quelle valeur. Pour cette raison, et de par les applications en simulation quantique, ces portes continues sont cruciales pour le calcul quantique, en particulier au niveau conceptuel des algorithmes quantiques. Pour parvenir à une implémentation matérielle tolérante aux pannes, elles seront finalement compilées en séquences de portes discrètes approximant ces rotations de façon très proche.