Le rôle des portes T et des usines T dans l’informatique quantique
Cet article décrit le rôle des portes T et des usines T dans l’informatique quantique tolérante aux pannes. Donner un algorithme quantique, l’estimation des ressources requises pour l’exécution des portes T et des usines T devient cruciale pour déterminer la faisabilité de l’algorithme. L’estimateur de ressources Azure Quantum calcule le nombre d’états T nécessaires pour exécuter l’algorithme, le nombre de qubits physiques pour une fabrique T unique et le runtime de la fabrique T.
Ensemble universel de portes quantiques
Selon les critères de DiVincenzo, un ordinateur quantique évolutif doit être en mesure d’implémenter un ensemble universel de portes quantiques. Un ensemble universel contient toutes les portes nécessaires pour effectuer tout calcul quantique, autrement dit, tout calcul doit se décomposer en une séquence finie de portes universelles. Au minimum, un ordinateur quantique doit être en mesure de déplacer des qubits uniques vers n’importe quelle position sur la sphère Bloch (à l’aide de portes à qubit unique), ainsi que d’introduire l’enchevêtrement dans le système, ce qui nécessite une porte multi-qubit.
Quatre fonctions seulement mappent un bit à un bit sur un ordinateur classique. En revanche, sur un ordinateur quantique, il existe un nombre infini de transformations unitaires sur un seul qubit. Par conséquent, aucun ensemble fini d’opérations quantiques primitives ou de portes, ne peut répliquer exactement l’ensemble infini de transformations unitaires autorisées dans l’informatique quantique. À la différence d’un ordinateur classique, un ordinateur quantique ne peut donc pas implémenter exactement chaque programme quantique possible avec un nombre fini de portes. Ainsi, les ordinateurs quantiques ne peuvent pas être universels au même titre que les ordinateurs classiques. Quand nous disons qu’un ensemble de portes est universel en informatique quantique, cela n’a donc pas précisément la même portée qu’en informatique classique.
Pour l’universalité, il est nécessaire qu’un ordinateur quantique se rapproche uniquement de chaque matrice unitaire dans une erreur finie à l’aide d’une séquence de porte de longueur finie.
En d’autres termes, un ensemble de portes est universel si une transformation unitaire quelconque peut être approximativement écrite comme produit des portes de cet ensemble. Il est nécessaire que pour toute erreur prescrite liée, il existe des portes $G_, G_{2}, \ldots, G_N$ de l’ensemble de portes{1} de telle sorte que
$$ G_N G_{N-1}\cdots G_2 G_1 \approx U. $$
Étant donné que la convention de multiplication de matrice consiste à multiplier de droite à gauche la première opération de porte dans cette séquence, $G_N$, est en fait la dernière appliquée au vecteur d’état quantique. Plus formellement, cet ensemble de portes est dit « universel » si, pour chaque tolérance d’erreur $\epsilon>0$, il existe $G_1, \ldots, G_N$ de sorte que la distance entre $G_N\ldots G_1$ et $U$ ne dépasse pas $\epsilon$. Dans l’idéal, la valeur de $N$ nécessaire pour atteindre cette distance d’$\epsilon$ doit croître de façon poly-logarithmique avec $1/\epsilon$.
Par exemple, l’ensemble formé par hadamard, CNOT et T gates est un ensemble universel, à partir duquel tout calcul quantique (sur n’importe quel nombre de qubits) peut être généré. Le Hadamard et le jeu de portes T génèrent n’importe quelle porte à qubit unique :
$$H=\frac{1}{\sqrt{ 1 amp ; 1 \\ & ;-1 \end{bmatrix}, \qquad T=\begin{bmatrix} 1 & ; 0 0 \\ & ; e^{i\pi/4.\end{bmatrix}}&{2}}\begin{bmatrix} $$
Dans un ordinateur quantique, les portes quantiques peuvent être classées en deux catégories : les portes clifford et les portes non-Clifford, dans ce cas, la porte T. Les programmes quantiques fabriqués à partir de seules portes Clifford peuvent être simulés efficacement à l’aide d’un ordinateur classique, et par conséquent, les portes non-Clifford sont requises pour obtenir un avantage quantique. Dans de nombreux schémas de correction d’erreurs quantiques (QEC), les portes de Clifford sont faciles à implémenter, c’est-à-dire qu’elles nécessitent très peu de ressources en termes d’opérations et de qubits pour implémenter la tolérance de panne, alors que les portes non-Clifford sont assez coûteuses lors de la nécessité d’une tolérance de panne. Dans un ensemble de portes quantiques universelles, la porte T est couramment utilisée comme porte non-Clifford.
L’ensemble standard de portes à qubit Clifford, inclus par défaut dans Q#, include
$$H=\frac{{2}}\begin{bmatrix}{1}{\sqrt{ 1 & ; 1 \\ & ;-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & ; 0 0 \\ & ; i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & ; 1 1 \\& ; 0 \end{bmatrix}= HT^4H,$$
$$ Y =\begin{bmatrix} 0 & ; -i \\ amp & ; 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1& ; 0\\ 0& ;-1 \end{bmatrix}=T^4. $$
Avec la porte non-Clifford (la porte T), ces opérations peuvent être composées de manière à estimer toute transformation unitaire sur un qubit unique.
Fabriques T dans l’estimateur de ressources Azure Quantum
La préparation de la porte non-Clifford T est cruciale car les autres portes quantiques ne sont pas suffisantes pour le calcul quantique universel. Pour implémenter des opérations non-Clifford pour des algorithmes à l’échelle pratique, des portes T à faible taux d’erreur (ou états T) sont requises. Toutefois, ils peuvent être difficiles à implémenter directement sur des qubits logiques et peuvent également être difficiles pour certains qubits physiques.
Dans un ordinateur quantique tolérant aux pannes, les états T de faible taux d’erreur requis sont produits à l’aide d’une fabrique de distillation d’état T ou D’usine T pour un court terme. Ces fabriques T impliquent généralement une séquence d’arrondis de distillation, où chaque tour prend de nombreux états T bruyants encodés dans un code de distance plus petit, les traite à l’aide d’une unité de distillation et génère moins d’états T bruyants encodés dans un code de distance plus grand, avec le nombre d’arrondis, d’unités de distillation et de distances qui peuvent être variées. Cette procédure est itérée, où les états T de sortie d’un tour sont alimentés dans le tour suivant en tant qu’entrées.
En fonction de la durée de la fabrique T, l’estimateur de ressources Azure Quantum détermine la fréquence à laquelle une fabrique T peut être appelée avant qu’elle dépasse le runtime total de l’algorithme, et ainsi le nombre d’états T pouvant être générés pendant le runtime de l’algorithme. En règle générale, plus d’états T sont requis que ce qui peut être produit dans les appels d’une fabrique T unique pendant le runtime de l’algorithme. Pour produire plus d’états T, l’estimateur de ressources utilise des copies des usines T.
Estimation physique de la fabrique T
L’estimateur de ressources calcule le nombre total d’états T nécessaires pour exécuter l’algorithme, ainsi que le nombre de qubits physiques pour une fabrique T unique et son runtime.
L’objectif est de produire tous les états T au sein du runtime d’algorithme avec le plus peu de copies de fabrique T que possible. Le diagramme suivant illustre un exemple du runtime de l’algorithme et du runtime d’une fabrique T. Vous pouvez voir que le runtime de la fabrique T est plus court que le runtime de l’algorithme. Dans cet exemple, une fabrique T peut distiller un état T. Deux questions se posent :
- À quelle fréquence la fabrique T peut-elle être appelée avant la fin de l’algorithme ?
- Combien de copies du cycle de distillation de la fabrique T sont nécessaires pour créer le nombre d’états T requis pendant le runtime de l’algorithme ?
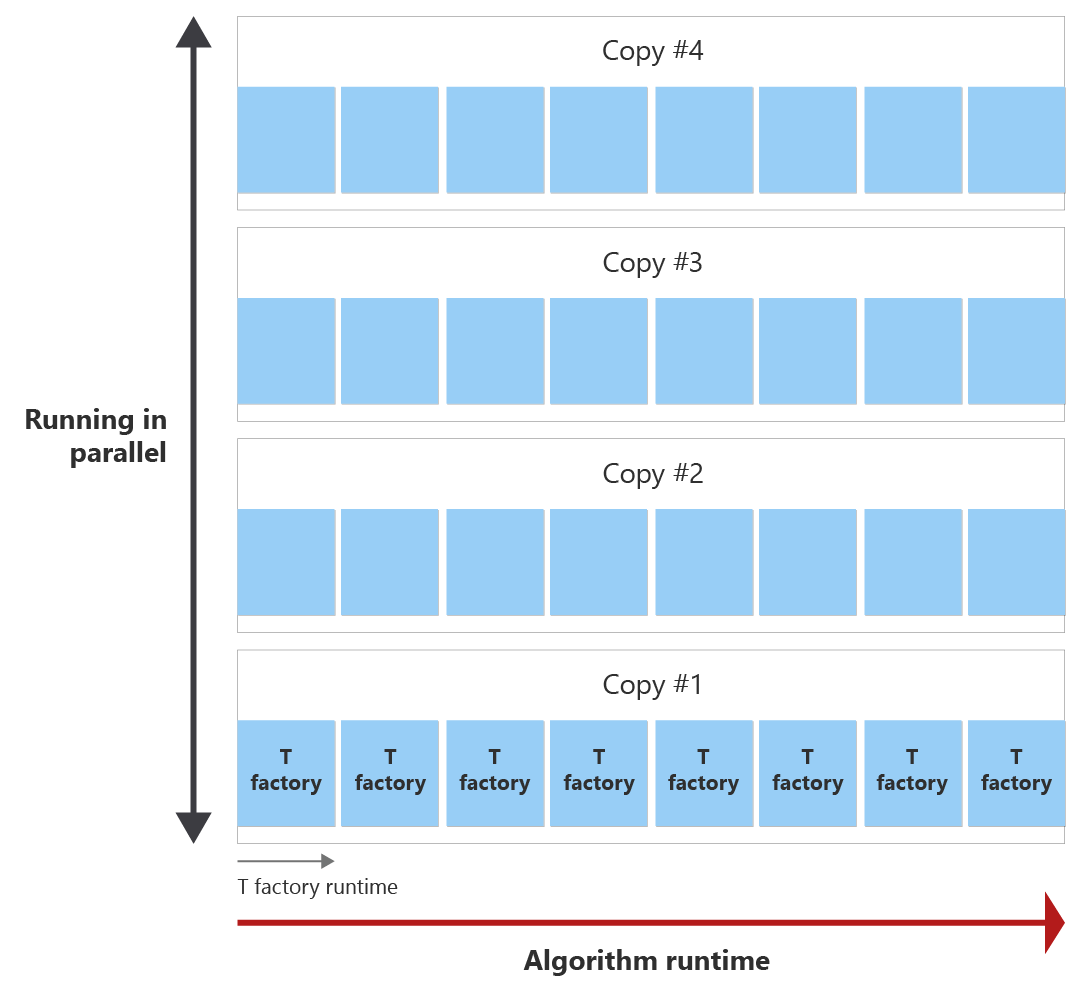
Avant la fin de l’algorithme, la fabrique T peut être appelée huit fois, ce qui est appelé round de distillation. Par exemple, si vous avez besoin de 30 états T, une fabrique T unique est appelée huit fois pendant l’exécution de l’algorithme et crée donc huit états T. Ensuite, vous avez besoin de quatre copies du cycle de distillation de la fabrique T en parallèle pour distiller les 30 états T nécessaires.
Remarque
Notez que les copies T factory et les appels de fabrique T ne sont pas les mêmes.
Les usines de distillation de l’état T sont implémentées dans une séquence d’arrondis, où chaque tour se compose d’un ensemble de copies d’unités de distillation s’exécutant en parallèle. L’estimateur de ressources calcule le nombre de qubits physiques nécessaires pour exécuter une fabrique T et la durée pendant laquelle la fabrique T s’exécute, entre autres paramètres requis.
Vous ne pouvez effectuer que des appels complets d’une fabrique T. Par conséquent, il peut arriver que le runtime cumulé de tous les appels de fabrique T soit inférieur au runtime d’algorithme. Étant donné que les qubits sont réutilisés par des arrondis différents, le nombre de qubits physiques pour une fabrique T est le nombre maximal de qubits physiques utilisés pour un tour. Le runtime de la fabrique T est la somme du runtime dans toutes les rondes.
Remarque
Si le taux d’erreur de porte T physique est inférieur au taux d’erreur d’état T logique requis, l’estimateur de ressources ne peut pas effectuer une bonne estimation des ressources. Lorsque vous envoyez un travail d’estimation des ressources, vous pouvez rencontrer que la fabrique T est introuvable, car le taux d’erreur d’état T logique requis est trop faible ou trop élevé.
Pour plus d’informations, consultez l’annexe C de l’évaluation des exigences pour effectuer une mise à l’échelle vers un avantage quantique pratique.