Ecuaciones PRT (Direct3D 9)

Para comprender completamente un sombreador que implementa PRT, resulta útil derivar la fórmula que usa el sombreador para calcular la radiación de salida.

Para empezar, la siguiente ecuación es la ecuación general para calcular la radiación de salida resultante de la iluminación directa en un objeto difuso con iluminación lejana arbitraria.

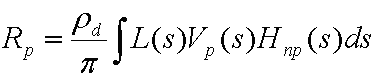
donde:

Parámetro	Descripción
Rp	Radiancia de salida en vértice p. Se evalúa en cada vértice de la malla.
pd	Albedo de la superficie.
pi	Constante, utilizada como factor de normalización de conservación de la energía.
L(s)	Entorno de iluminación (radiancia de origen).
Vp₍s₎	Función de visibilidad binaria para point p. Es 1 si el punto puede ver la luz, 0 si no.
Hnp₍s₎	El término coseno de la ley de Lambert. Igual a max((Np·s), 0) donde Np es la superficie normal en el punto p.
s	Variable que se integra sobre la esfera.

 

Con funciones de base esféricas, como armónicos esféricos, la siguiente ecuación aproxima el entorno de iluminación.

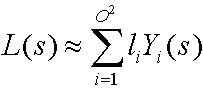
donde:

Parámetro	Descripción
L(s)	Entorno de iluminación (radiancia de origen).
i	Entero que suma el número de funciones base.
O	El orden de los armónicos esféricos.
li	Coeficiente.
Yi(s)	Alguna función base sobre la esfera.

 

La colección de estos coeficientes, L', proporciona la aproximación óptima para las L(s) de función con las funciones base Y(s). Sustituir y distribuir produce la siguiente ecuación.

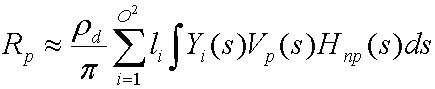
La integral de Y_i(s)Vp₍s₎Hnp₍s₎ es un coeficiente de transferencia t_pi que el simulador precompute para cada vértice de la malla. Sustituir esto produce la siguiente ecuación.

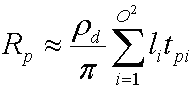
Al cambiar esto a la notación vectorial, se produce la siguiente ecuación sin comprimir para calcular la radiación de salida para cada canal.

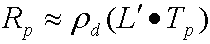
donde:

Parámetro	Descripción
Rp	Radiancia de salida en vértice p.
pd	Albedo de la superficie.
L'	El vector de li, y es la proyección de la radiación de origen en las funciones armónicas esféricas. Se trata de un vector order² de coeficientes armónicos esféricos.
Tp	Vector de transferencia order² para vértice p. El simulador divide los coeficientes de transferencia por p.

 

Ambos vectores son un vector order² de coeficientes armónicos esféricos, por lo que observe que esto es simplemente un producto de puntos. Dependiendo del orden, el punto puede ser costoso, por lo que se puede usar la compresión. Un algoritmo denominado Análisis de componentes principales agrupados (CPCA) comprime eficazmente los datos. Esto permite el uso de una aproximación armónica esférica de orden superior que da como resultado sombras más nítidas.

CPCA proporciona la siguiente ecuación para aproximar el vector de transferencia.

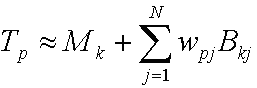
donde:

Parámetro	Descripción
Tp	Vector de transferencia para vértice p.
Mk	Media para el clúster k.
j	Entero que suma el número de vectores PCA.
No	Número de vectores PCA.
wpj	Peso pcA jth para el punto p.
Bkj	Vector de base pcA jth para el clúster k.

 

Un clúster es simplemente un número de vértices que comparten el mismo vector medio. A continuación se describe cómo obtener la media del clúster, las ponderaciones de PCA, los vectores de base de PCA y los identificadores de clúster de los vértices.

Sustituir estas dos ecuaciones produce:

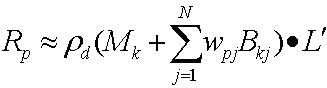
Después, la distribución del producto de puntos produce la siguiente ecuación.

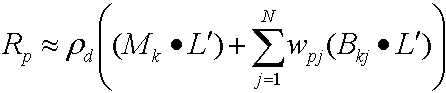
Porque ambos (Mk· L') y (B_kj· L') son constantes por vértice, la muestra calcula estos valores con la CPU y los pasa como constantes al sombreador de vértices; dado que w_pj cambia para cada vértice, el ejemplo almacena estos datos por vértice en el búfer de vértices.

Temas relacionados

Transferencia de radiancia precalada