Compartir a través de

Transferencia radiance precalada (Direct3D 9)

  • Artículo

Uso de la transferencia radiance precalada

Hay varias formas de complejidad presentes en escenas interesantes, incluida la forma en que se modela el entorno de iluminación (es decir, los modelos de iluminación de área frente a los de punto y dirección) y qué tipo de efectos globales se modelan (por ejemplo, sombras, interreflections, dispersión de subsurface). Las técnicas de representación interactiva tradicionales modelarán una cantidad limitada de esta complejidad. PRT permite estos efectos con algunas restricciones significativas:

  • Se supone que los objetos son rígidos (es decir, no hay deformaciones).
  • Se trata de un enfoque centrado en objetos (a menos que los objetos se muevan juntos, estos efectos globales no se mantienen entre ellos).
  • Solo se modela la iluminación de baja frecuencia (lo que da lugar a sombras suaves). Para las luces de alta frecuencia (sombras nítidas), las técnicas tradicionales tendrían que emplearse.

PRT requiere uno de los siguientes elementos, pero no ambos:

  • modelos altamente teselados y vs_1_1
  • ps_2_0

Iluminación difusa estándar frente a PRT

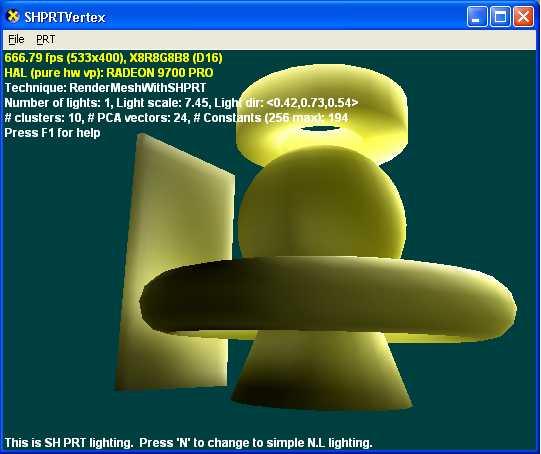
La ilustración siguiente se representa con el modelo de iluminación tradicional (n · l). Las sombras afiladas podrían habilitarse mediante otro paso y alguna forma de técnica de sombreado (mapas de profundidad de sombras o volúmenes de sombra). Agregar varias luces requeriría varios pases (si se van a usar sombras) o sombreadores más complejos con técnicas tradicionales.

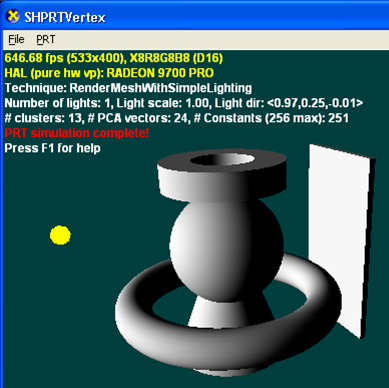
captura de pantalla de una ilustración representada mediante el modelo de iluminación tradicional

La siguiente ilustración se representa con PRT mediante la mejor aproximación de una sola luz direccional que puede resolver. Esto da como resultado sombras suaves que serían difíciles de producir con técnicas tradicionales. Dado que PRT siempre modela entornos de iluminación completos agregando varias luces o usando un mapa de entorno, solo cambiaría los valores (pero no el número) de constantes usadas por el sombreador.

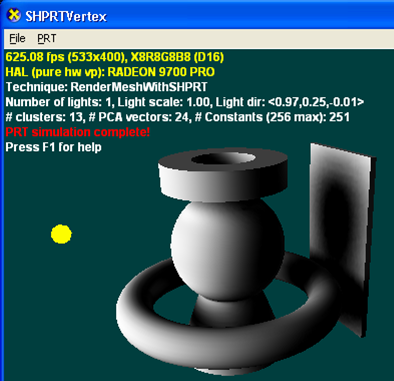
captura de pantalla de una ilustración representada mediante prt

PRT con interreflections

La iluminación directa llega a la superficie directamente desde la luz. Las interreflecciones son ligeras que llegan a la superficie después de rebotar alguna otra superficie algunas veces. PRT puede modelar este comportamiento sin cambiar el rendimiento en tiempo de ejecución simplemente ejecutando el simulador con parámetros diferentes.

La ilustración siguiente se crea solo con PRT directo (0 rebotes sin interreflections).

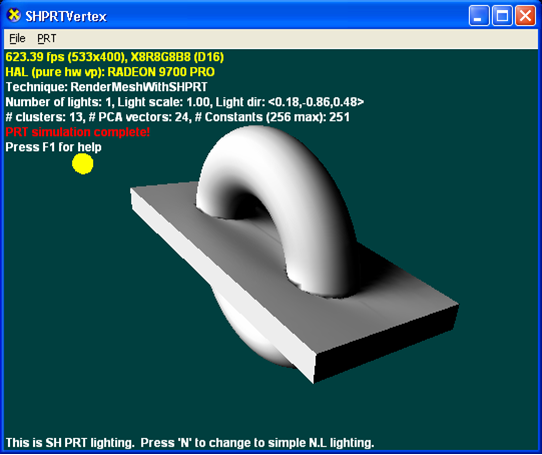
captura de pantalla de una ilustración representada solo con prt directo

La ilustración siguiente se crea mediante PRT con interreflections (2 rebotes con interreflections).

captura de pantalla de una ilustración representada mediante prt con interreflections

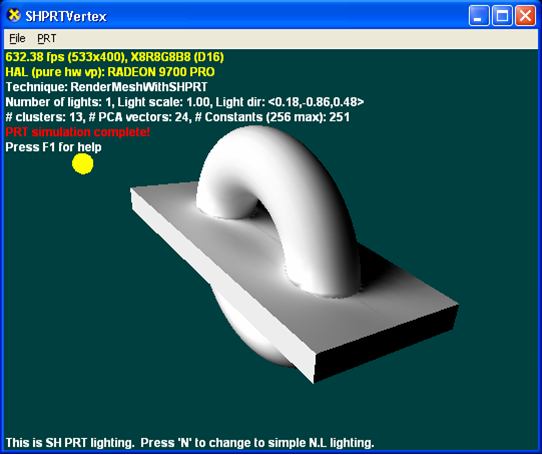
PRT con dispersión de subsurface

La dispersión de subsurface es una técnica que modela cómo pasa la luz a través de determinados materiales. Por ejemplo, presione una linterna iluminada contra la palma de la mano. La luz de la linterna pasa a través de la mano, rebota alrededor (cambiando el color en el proceso) y sale del otro lado de la mano. Esto también se puede modelar con cambios simples en el simulador y sin cambios en el entorno de ejecución.

En la ilustración siguiente se muestra PRT con dispersión de subsurface.

captura de pantalla de una ilustración representada mediante prt con dispersión de subsurface

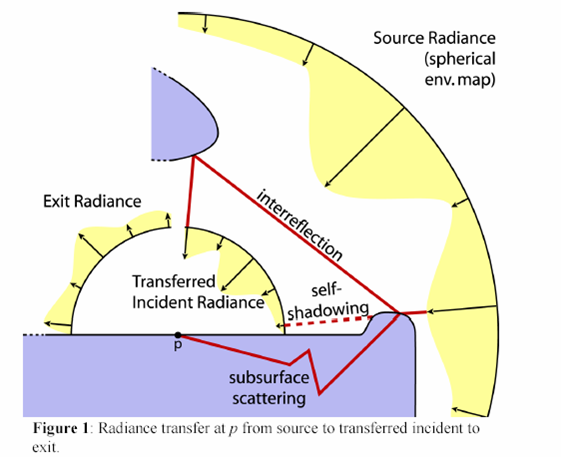
Cómo funciona PRT

Los términos siguientes son útiles para comprender cómo funciona PRT, como se muestra en el diagrama siguiente.

Radiance de origen: la radiación de origen representa el entorno de iluminación en su conjunto. En PRT, un entorno arbitrario se aproxima mediante la base armónica esférica: se supone que esta iluminación es lejana con respecto al objeto (la misma suposición que se realiza con mapas de entorno).

Radiancia de salida: La radiación de salida es la luz que sale de un punto en la superficie desde cualquier fuente posible (radiancia reflejada, dispersión de subsurface, emisión).

Vectores de transferencia: los vectores de transferencia asignan Radiance de origen a la radiación de salida y se precalulan sin conexión mediante una simulación de transporte de luz compleja.

diagrama de cómo funciona prt

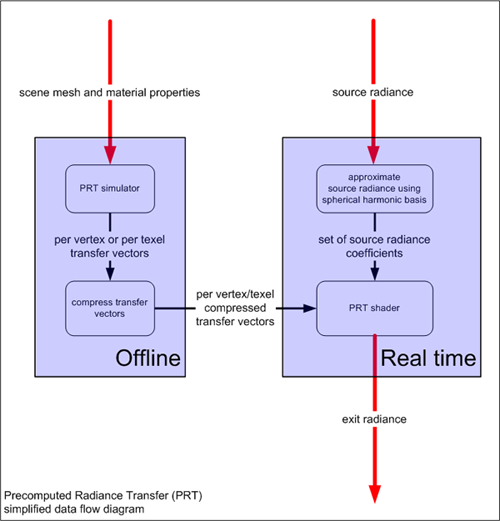
PRT factoriza el proceso de representación en dos fases, como se muestra en el diagrama siguiente:

  1. Una simulación de transporte ligero costosa precompute los coeficientes de transferencia que se pueden usar en tiempo de ejecución.
  2. Una fase en tiempo de ejecución relativamente ligera se aproxima primero al entorno de iluminación utilizando la base armónica esférica, luego usa estos coeficientes de iluminación y los coeficientes de transferencia precalculados (de la fase 1) con un sombreador simple, lo que da lugar a radiancia de salida (la luz que sale del objeto).

diagrama del flujo de datos prt

Uso de la API de PRT

  1. Calcule los vectores de transferencia con uno de los procesos... métodos de ID3DXPRTEngine.

    El tratamiento directo con estos vectores de transferencia requiere una cantidad significativa de cálculo de memoria y sombreador. La compresión reduce significativamente la cantidad de memoria y cálculo del sombreador necesarios.

    Los valores de iluminación finales se calculan en un sombreador de vértices que implementa la siguiente ecuación de representación comprimida.

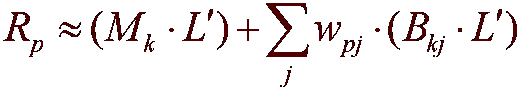
    ecuación de representación prt

    Donde:

    Parámetro Descripción
    Rp Un único canal de radiancia de salida en vértice p y se evalúa en cada vértice de la malla.
    Mk Media para el clúster k. Se trata de un vector Order² de coeficientes.
    k Identificador de clúster para vértice p.
    L' La aproximación de la radiación de origen en las funciones de base SH. Se trata de un vector Order² de coeficientes.
    j Entero que suma el número de vectores PCA.
    wpj Peso pcA jth para punto p. Se trata de un único coeficiente.
    Bkj Vector de base pcA jth para el clúster k. Se trata de un vector Order² de coeficientes.

     

    El extracto... Los métodos de ID3DXPRTCompBuffer proporcionan acceso a los datos comprimidos de la simulación.

  2. Calcule la radiación de origen.

    Hay varias funciones auxiliares en la API para controlar una variedad de escenarios de iluminación comunes.

    Función Finalidad
    D3DXSHEvalDirectionalLight Aproxima una luz direccional convencional.
    D3DXSHEvalsphericalLight Aproxima las fuentes de luz esféricas locales. (Tenga en cuenta que PRT solo funciona con entornos de iluminación a distancia).
    D3DXSHEvalConeLight Se aproxima a una fuente de luz de área lejana. Un ejemplo sería el sol (ángulo de cono muy pequeño).
    D3DXSHEvalHemisphereLight Evalúa una luz que es una interpolación lineal entre dos colores (uno en cada polo de una esfera).

     

  3. Calcule la radiación de salida.

    La ecuación 1 ahora tiene que evaluarse en cada punto mediante un sombreador de vértices o píxeles. Para poder evaluar el sombreador, las constantes deben calcularse previamente y cargarse en la tabla de constantes (consulte el ejemplo de demostración de PRT para obtener más información). El propio sombreador es una implementación sencilla de esta ecuación.

    struct VS_OUTPUT
{
    float4 Position   : POSITION;   // vertex position 
    float2 TextureUV  : TEXCOORD0;  // vertex texture coordinates 
    float4 Diffuse    : COLOR0;     // vertex diffuse color
};

VS_OUTPUT Output;   
Output.Position = mul(vPos, mWorldViewProjection);

float4 vExitR = float4(0,0,0,0);
float4 vExitG = float4(0,0,0,0);
float4 vExitB = float4(0,0,0,0);

for (int i=0; i < (NUM_PCA_VECTORS/4); i++) 
{
   vExitR += vPCAWeights[i] * 
       vClusteredPCA[iClusterOffset+i+1+(NUM_PCA_VECTORS/4)*0];
   vExitG += vPCAWeights[i] * 
       vClusteredPCA[iClusterOffset+i+1+(NUM_PCA_VECTORS/4)*1];
   vExitB += vPCAWeights[i] * 
       vClusteredPCA[iClusterOffset+i+1+(NUM_PCA_VECTORS/4)*2];
}

float4 vExitRadiance = vClusteredPCA[iClusterOffset];
vExitRadiance.r += dot(vExitR,1);
vExitRadiance.g += dot(vExitG,1);
vExitRadiance.b += dot(vExitB,1);

Output.Diffuse = vExitRadiance;

Referencias

Para obtener más información sobre PRT y armónicos esféricos, consulte los siguientes artículos:

Precomputed Radiance Transfer for Real-Time Rendering in Dynamic, 
Low-Frequency Lighting Environments 
P.-P. Sloan, J. Kautz, J. Snyder
SIGGRAPH 2002 

Clustered Principal Components for Precomputed Radiance Transfer 
P.-P. Sloan, J. Hall, J. Hart, J. Snyder 
SIGGRAPH 2003 

Efficient Evaluation of Irradiance Environment Maps 
P.-P. Sloan 
ShaderX 2,  W. Engel 

Spherical Harmonic Lighting: The Gritty Details 
R. Green 
GDC 2003 

An Efficient Representation for Irradiance Environment Maps 
R. Ramamoorthi, P. Hanrahan 

A Practical Model for Subsurface Light Transport 
H. W. Jensen, S. R. Marschner, M. Levoy, and P. Hanrahan 
SIGGRAPH 2001 

Bi-Scale Radiance Transfer 
P.-P. Sloan, X. Liu, H.-Y. Shum, J. Snyder
SIGGRAPH 2003 

Fast, Arbitrary BRDF Shading for Low-Frequency Lighting Using Spherical 
Harmonics 
J. Kautz, P.-P. Sloan, J. Snyder
12th Eurographics Workshop on Rendering 

Precomputing Interactive Dynamic Deformable Scenes 
D. James, K. Fatahalian 
SIGGRAPH 2003 

All-Frequency Shadows Using Non-linear Wavelet Lighting Approximation 
R. Ng, R. Ramamoorth, P. Hanrahan 
SIGGRAPH 2003 

Matrix Radiance Transfer 
J. Lehtinen, J. Kautz
SIGGRAPH 2003 

Math World 
E. W. Weisstein, Wolfram Research, Inc. 

Quantum Theory of Angular Momentum 
D. A. Varshalovich, A.N. Moskalev, V.K. Khersonskii

Temas avanzados

Ecuaciones PRT (Direct3D 9)

Representar PRT con texturas (Direct3D 9)

ID3DXPRTBuffer

ID3DXPRTCompBuffer

ID3DXPRTEngine

ID3DXTextureGutterHelper

Funciones de transferencia radiance precaladas

Funciones matemáticas