Transformaciones no afines
Crear efectos de perspectiva y cónicos con la tercera columna de la matriz de transformación
Todas las transformaciones de traslación, escalado, rotación y distorsión se clasifican como transformaciones afines. Las transformaciones afines conservan las líneas paralelas. Si dos líneas son paralelas antes de la transformación, siguen siéndolo después de la transformación. Los rectángulos siempre se transforman en paralelogramos.
Sin embargo, SkiaSharp también es capaz de transformaciones no afines, que tienen la capacidad de transformar un rectángulo en cualquier cuadrilátero convexo:

Un cuadrilátero convexo es una figura de cuatro caras con ángulos interiores siempre inferiores a 180 grados y lados que no se cruzan entre sí.
Las transformaciones no afines ocurren cuando la tercera fila de la matriz de transformación se establece en valores distintos de 0, 0 y 1. La multiplicación completa de SKMatrix es:
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z' |
│ TransX TransY Persp2 │
Las fórmulas de transformación resultantes son:
x' = ScaleX·x + SkewX·y + TransX
y' = SkewY·x + ScaleY·y + TransY
z` = Persp0·x + Persp1·y + Persp2
La regla fundamental de usar una matriz de 3 x 3 para transformaciones bidimensionales es que todo permanece en el plano donde Z es igual a 1. A no ser que Persp0 y Persp1 sean 0 y Persp2 sea igual a 1, la transformación moverá las coordenadas Z fuera de ese plano.
Para restaurarlo a una transformación bidimensional, las coordenadas se deben mover de nuevo a ese plano. Se requiere otro paso. Los valores x', y', y z' deben dividirse por z':
x" = x' / z'
y" = y' / z'
z" = z' / z' = 1
Estas son conocidas como coordenadas homogéneas y fueron desarrolladas por el matemático August Fernando Möbius, mucho más conocido por su paradoja de topología, la tira de Möbius.
Si z' es 0, la división da como resultado coordenadas infinitas. De hecho, una de las motivaciones de Möbius para desarrollar coordenadas homogéneas era la capacidad de representar valores infinitos con números finitos.
Sin embargo, al mostrar gráficos, queremos evitar representar algo con coordenadas que se transforman en valores infinitos. Esas coordenadas no se representarán. Todo lo que se encuentra en las proximidades de esas coordenadas será muy grande y probablemente no coherente visualmente.
En esta ecuación, no queremos que el valor de z' se convierta en cero:
z` = Persp0·x + Persp1·y + Persp2
Por consiguiente, estos valores tienen algunas restricciones prácticas:
La celda Persp2 puede ser cero o no ser cero. Si Persp2 es cero, z' es cero para el punto (0, 0) y normalmente no es lo que buscamos, porque ese punto es muy común en gráficos bidimensionales. Si Persp2 no es igual a cero, no se pierde la generalidad si Persp2 se fija en 1. Por ejemplo, si determina que Persp2 debe ser 5, simplemente puede dividir todas las celdas de la matriz en 5, lo que hace Persp2 igual a 1 y el resultado será el mismo.
Por estas razones, Persp2 a menudo se fija en 1, que es el mismo valor en la matriz de identidad.
Por lo general, Persp0 y Persp1 son números pequeños. Por ejemplo, supongamos que comienza con una matriz de identidades, pero establece Persp0 en 0.01:
| 1 0 0.01 | | 0 1 0 | | 0 0 1 |
Las fórmulas de transformación son:
x' = x / (0,01·x + 1)
y' = y / (0.01·x + 1)
Ahora use esta transformación para representar un cuadro de 100 píxeles colocado en el origen. Así es como se transforman las cuatro esquinas:
(0, 0) → (0, 0)
(0, 100) → (0, 100)
(100, 0) → (50, 0)
(100, 100) → (50, 50)
Cuando x es 100, el denominador z' es 2, por lo que las coordenadas x e y se dividen a la mitad. El lado derecho del cuadro se vuelve más corto que el lado izquierdo:
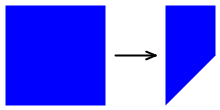
La parte Persp de estos nombres de celda hace referencia a "perspectiva", porque el escorzo sugiere que el cuadro ahora está inclinado con el lado derecho más allá de la persona que lo mira.
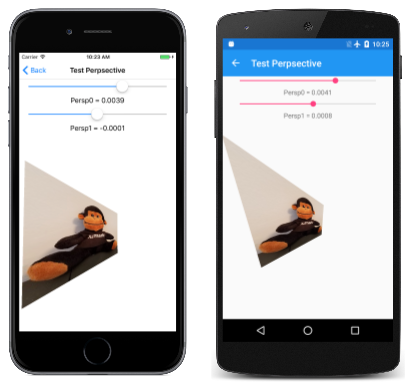
La página Perspectiva de prueba le permite experimentar con valores de Persp0 y Pers1 y desarrollar su intuición sobre cómo funcionan. Los valores razonables de estas celdas de matriz son tan pequeños que el Slider de la Plataforma universal de Windows no puede controlarlos correctamente. Para solucionar este problema con la UWP, los dos elementos Slider del archivo TestPerspective.xaml deben inicializarse para que oscilen entre –1 y 1:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.TestPerspectivePage"
Title="Test Perpsective">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Minimum" Value="-1" />
<Setter Property="Maximum" Value="1" />
<Setter Property="Margin" Value="20, 0" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="persp0Slider"
Grid.Row="0"
ValueChanged="OnPersp0SliderValueChanged" />
<Label x:Name="persp0Label"
Text="Persp0 = 0.0000"
Grid.Row="1" />
<Slider x:Name="persp1Slider"
Grid.Row="2"
ValueChanged="OnPersp1SliderValueChanged" />
<Label x:Name="persp1Label"
Text="Persp1 = 0.0000"
Grid.Row="3" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="4"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Los controladores de eventos de los controles deslizantes del archivo de código subyacente de TestPerspectivePage dividen los valores en 100 para que oscilan entre –0,01 y 0,01. Además, el constructor se carga en un mapa de bits:
public partial class TestPerspectivePage : ContentPage
{
SKBitmap bitmap;
public TestPerspectivePage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnPersp0SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp0Label.Text = String.Format("Persp0 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
void OnPersp1SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp1Label.Text = String.Format("Persp1 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
...
}
El controlador PaintSurface calcula un valor SKMatrix denominado perspectiveMatrix en función de los valores de estos dos controles deslizantes divididos por 100. Esto se combina con dos transformaciones de traslación que colocan el centro de esta transformación en el centro del mapa de bits:
public partial class TestPerspectivePage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Calculate perspective matrix
SKMatrix perspectiveMatrix = SKMatrix.MakeIdentity();
perspectiveMatrix.Persp0 = (float)persp0Slider.Value / 100;
perspectiveMatrix.Persp1 = (float)persp1Slider.Value / 100;
// Center of screen
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
SKMatrix.PostConcat(ref matrix, perspectiveMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(xCenter, yCenter));
// Coordinates to center bitmap on canvas
float x = xCenter - bitmap.Width / 2;
float y = yCenter - bitmap.Height / 2;
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
}
Estas son algunas imágenes de ejemplo:
A medida que experimente con los controles deslizantes, encontrará que los valores más allá de 0,0066 o por debajo de –0,0066 hacen que la imagen se fracture y sea incoherente de repente. El mapa de bits que se va a transformar es un cuadrado de 300 píxeles. Se transforma en relación con su centro, por lo que las coordenadas del intervalo de mapa de bits van de –150 a 150. Recuerde que el valor de z' es:
z` = Persp0·x + Persp1·y + 1
Si Persp0 o Persp1 es mayor que 0,0066 o inferior a –0,0066, siempre hay alguna coordenada del mapa de bits que da como resultado un valor z de cero. Esto provoca divisiones por cero y la representación se convierte en un desastre. Al usar transformaciones no afines, queremos evitar representar algo con coordenadas que provoque la división por cero.
Por lo general, no establecerá Persp0 ni Persp1 se aislará. También es necesario establecer otras celdas en la matriz para lograr ciertos tipos de transformaciones no afines.
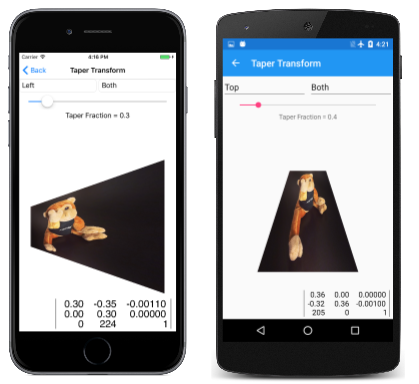
Un ejemplo de transformación no afín es una transformación cónica. Este tipo de transformación no afín conserva las dimensiones generales de un rectángulo, pero reduce un lado:
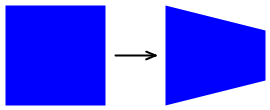
La clase TaperTransform realiza un cálculo generalizado de una transformación no afín basada en estos parámetros:
- el tamaño rectangular de la imagen que se va a transformar.
- una enumeración que indica el lado del rectángulo que se reduce,
- otra enumeración que indica cómo se hace la transformación cónica
- la extensión de la transformación cónica.
Este es el código :
enum TaperSide { Left, Top, Right, Bottom }
enum TaperCorner { LeftOrTop, RightOrBottom, Both }
static class TaperTransform
{
public static SKMatrix Make(SKSize size, TaperSide taperSide, TaperCorner taperCorner, float taperFraction)
{
SKMatrix matrix = SKMatrix.MakeIdentity();
switch (taperSide)
{
case TaperSide.Left:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp0 = (taperFraction - 1) / size.Width;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Top:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp1 = (taperFraction - 1) / size.Height;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Right:
matrix.ScaleX = 1 / taperFraction;
matrix.Persp0 = (1 - taperFraction) / (size.Width * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
break;
}
break;
case TaperSide.Bottom:
matrix.ScaleY = 1 / taperFraction;
matrix.Persp1 = (1 - taperFraction) / (size.Height * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
break;
}
break;
}
return matrix;
}
}
Esta clase se usa en la página Transformación cónica. El archivo XAML crea una instancia de dos elementos Picker para seleccionar los valores de enumeración y un Slider para elegir la fracción de transformación cónica. El controlador PaintSurface combina la transformación cónica con dos transformaciones de traslación para convertir la transformación en relación con la esquina superior izquierda del mapa de bits:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
TaperSide taperSide = (TaperSide)taperSidePicker.SelectedItem;
TaperCorner taperCorner = (TaperCorner)taperCornerPicker.SelectedItem;
float taperFraction = (float)taperFractionSlider.Value;
SKMatrix taperMatrix =
TaperTransform.Make(new SKSize(bitmap.Width, bitmap.Height),
taperSide, taperCorner, taperFraction);
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(taperMatrix);
matrixDisplay.Paint(canvas, taperMatrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Center bitmap on canvas
float x = (info.Width - bitmap.Width) / 2;
float y = (info.Height - bitmap.Height) / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-x, -y);
SKMatrix.PostConcat(ref matrix, taperMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(x, y));
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
Estos son algunos ejemplos:
Otro tipo de transformaciones no afines generalizadas es la rotación en 3D, que se muestra en el siguiente artículo Rotaciones 3D.
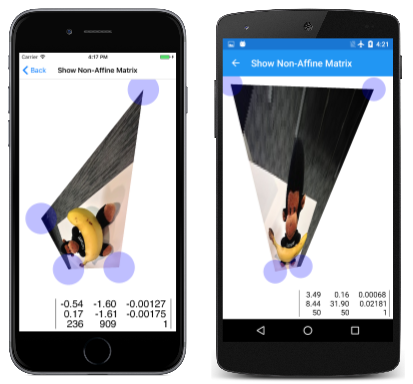
Una transformación no afín puede transformar un rectángulo en cualquier cuadrilátero convexo. Esto se muestra en la página Mostrar matriz no afín. Es muy similar a la página Mostrar matriz afín del artículo Transformaciones de matriz, excepto que tiene un cuarto objeto TouchPoint para manipular la cuarta esquina del mapa de bits:
Siempre que no haga que un ángulo interior de una de las esquinas del mapa de bits sea superior a 180 grados, o que dos lados se crucen entre sí, el programa calcula correctamente la transformación mediante este método de la clase ShowNonAffineMatrixPage:
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL, SKPoint ptLR)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
// Non-Affine transform
SKMatrix inverseA;
A.TryInvert(out inverseA);
SKPoint abPoint = inverseA.MapPoint(ptLR);
float a = abPoint.X;
float b = abPoint.Y;
float scaleX = a / (a + b - 1);
float scaleY = b / (a + b - 1);
SKMatrix N = new SKMatrix
{
ScaleX = scaleX,
ScaleY = scaleY,
Persp0 = scaleX - 1,
Persp1 = scaleY - 1,
Persp2 = 1
};
// Multiply S * N * A
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.PostConcat(ref result, S);
SKMatrix.PostConcat(ref result, N);
SKMatrix.PostConcat(ref result, A);
return result;
}
Para facilitar el cálculo, este método obtiene la transformación total como producto de tres transformaciones independientes, que se simbolizan aquí con flechas que muestran cómo estas transformaciones modifican las cuatro esquinas del mapa de bits:
(0, 0) → (0, 0) → (0, 0) → (x0, y0) (superior izquierda)
(0, H) → (0, 1) → (0, 1) → (x1, y1) (inferior izquierda)
(W, 0) → (1, 0) → (1, 0) → (x2, y2) (superior derecha)
(W, H) → (1, 1) → (a, b) → (x3, y3) (inferior derecha)
Las coordenadas finales a la derecha son los cuatro puntos asociados a los cuatro puntos táctiles. Estas son las coordenadas finales de las esquinas del mapa de bits.
W y H representan el ancho y el alto del mapa de bits. La primera transformación S simplemente escala el mapa de bits a un cuadrado de 1 píxel. La segunda transformación es la transformación no afín N y la tercera es la transformación afín A. Esa transformación afín se basa en tres puntos, por lo que es igual que el método afín ComputeMatrix anterior y no implica la cuarta fila con el punto (a, b).
Los valores a y b se calculan para que la tercera transformación sea afín. El código obtiene el inverso de la transformación afín y, a continuación, lo usa para asignar la esquina inferior derecha. Ese es el punto (a, b).
Otro uso de transformaciones no afines es imitar gráficos tridimensionales. En el siguiente artículo, Rotaciones 3D verá cómo girar un gráfico bidimensional en un espacio 3D.