Transformaciones de matriz en SkiaSharp
Profundice en las transformaciones de SkiaSharp con la versátil matriz de transformación
Todas las transformaciones aplicadas al objeto SKCanvas se consolidan en una sola instancia de la estructura SKMatrix. Se trata de una matriz de transformación estándar de 3 a 3 similar a la de todos los sistemas gráficos 2D modernos.
Como ha visto, puede usar transformaciones en SkiaSharp sin conocer la matriz de transformación, pero la matriz de transformación es importante desde una perspectiva teórica, y es fundamental al usar transformaciones para modificar rutas de acceso o para controlar entradas táctiles complejas, que se muestran en este artículo y en la siguiente.

La matriz de transformación actual aplicada a la SKCanvas está disponible en cualquier momento accediendo a la propiedad TotalMatrix de solo lectura. Puede establecer una nueva matriz de transformación mediante el método SetMatrix y puede restaurar esa matriz en valores predeterminados llamando a ResetMatrix.
El único miembro de SKCanvas que funciona directamente con la transformación de matriz del lienzo es Concat que concatena dos matrices multiplicándolas juntas.
La matriz de transformación predeterminada es la matriz de identidad y consta de varios 1 en las celdas diagonales y 0 en cualquier otra parte:
| 1 0 0 | | 0 1 0 | | 0 0 1 |
Puede crear una matriz de identidades mediante el método estático SKMatrix.MakeIdentity:
SKMatrix matrix = SKMatrix.MakeIdentity();
El constructor predeterminado SKMatrixno devuelve una matriz de identidades. Devuelve una matriz con todas las celdas establecidas en cero. No use el constructor SKMatrix a menos que planee establecer esas celdas manualmente.
Cuando SkiaSharp representa un objeto gráfico, cada punto (x, y) se convierte eficazmente en una matriz de 1 a 3 con un 1 en la tercera columna:
| x y 1 |
Esta matriz de 1 a 3 representa un punto tridimensional con la coordenada Z establecida en 1. Hay razones matemáticas (descritas más adelante) por las que una transformación de matriz bidimensional requiere trabajar en tres dimensiones. Puede pensar en esta matriz de 1 a 3 como que representa un punto en un sistema de coordenadas 3D, pero siempre en el plano 2D donde Z es igual a 1.
Esta matriz de 1 a 3 se multiplica por la matriz de transformación y el resultado es el punto representado en el lienzo:
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
Con la multiplicación de matriz estándar, los puntos convertidos son los siguientes:
x' = x
y' = y
z' = 1
Esa es la transformación predeterminada.
Cuando se llama al método Translate en el objeto SKCanvas, los argumentos tx y ty en el método Translate se convierten en las dos primeras celdas de la tercera fila de la matriz de transformación:
| 1 0 0 | | 0 1 0 | | tx ty 1 |
La multiplicación es ahora la siguiente:
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| tx ty 1 |
Estas son las fórmulas de transformación:
x' = x + tx
y' = y + ty
Los factores de escalado tienen un valor predeterminado de 1. Al llamar al método Scale en un nuevo objeto SKCanvas, la matriz de transformación resultante contiene los argumentos sx y sy en las celdas diagonales:
| sx 0 0 |
| x y 1 | × | 0 sy 0 | = | x' y' z' |
| 0 0 1 |
Las fórmulas de transformación son las siguientes:
x' = sx · x
y' = sy · y
La matriz de transformación después de llamar a Skew contiene los dos argumentos de las celdas de matriz adyacentes a los factores de escalado:
│ 1 ySkew 0 │
| x y 1 | × │ xSkew 1 0 │ = | x' y' z' |
│ 0 0 1 │
Las fórmulas de transformación son:
x' = x + xSkew · y
y' = ySkew · x + y
Para una llamada a RotateDegrees o RotateRadians para un ángulo de α, la matriz de transformación es la siguiente:
│ cos(α) sin(α) 0 │
| x y 1 | × │ –sin(α) cos(α) 0 │ = | x' y' z' |
│ 0 0 1 │
Estas son las fórmulas de transformación:
x' = cos(α) · x - sin(α) · y
y' = sin(α) · x - cos(α) · y
Cuando α es de 0 grados, es la matriz de identidad. Cuando α es de 180 grados, la matriz de transformación es la siguiente:
| –1 0 0 | | 0 –1 0 | | 0 0 1 |
Un giro de 180 grados equivale a voltear un objeto horizontal y verticalmente, lo que también se logra estableciendo factores de escala de –1.
Todos estos tipos de transformaciones se clasifican como transformaciones afín. Las transformaciones afín nunca implican la tercera columna de la matriz, que permanece en los valores predeterminados de 0, 0 y 1. En el artículo Transformaciones no afines se describen las transformaciones no afines.
Multiplicación de matrices
Una ventaja importante con el uso de la matriz de transformación es que las transformaciones compuestas se pueden obtener mediante la multiplicación de matrices, que a menudo se conoce en la documentación de SkiaSharp como concatenación. Muchos de los métodos relacionados con la transformación de SKCanvas hacen referencia a la "preconcatenación" o "preconcat". Esto hace referencia al orden de multiplicación, que es importante porque la multiplicación de matriz no es conmutativa.
Por ejemplo, la documentación del método Translate dice que "Preconcatena la matriz actual con la traducción especificada", mientras que la documentación del método Scale dice que "Preconcatena la matriz actual con la escala especificada".
Esto significa que la transformación especificada por la llamada al método es el multiplicador (el operando izquierdo) y la matriz de transformación actual es la multiplicada (el operando derecho).
Supongamos que se llama a Translate seguido de Scale:
canvas.Translate(tx, ty);
canvas.Scale(sx, sy);
La transformación Scale se multiplica por la transformación Translate para la matriz de transformación compuesta:
| sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | 0 0 1 | | tx ty 1 | | tx ty 1 |
Scale podría llamarse antes de Translate de la siguiente manera:
canvas.Scale(sx, sy);
canvas.Translate(tx, ty);
En ese caso, el orden de la multiplicación se invierte y los factores de escalado se aplican eficazmente a los factores de traducción:
| 1 0 0 | | sx 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | = | 0 sy 0 | | tx ty 1 | | 0 0 1 | | tx·sx ty·sy 1 |
Este es el método Scale con un punto dinámico:
canvas.Scale(sx, sy, px, py);
Esto equivale a las siguientes llamadas de traducción y escala:
canvas.Translate(px, py);
canvas.Scale(sx, sy);
canvas.Translate(–px, –py);
Las tres matrices de transformación se multiplican en orden inverso a partir de cómo aparecen los métodos en el código:
| 1 0 0 | | sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | –px –py 1 | | 0 0 1 | | px py 1 | | px–px·sx py–py·sy 1 |
La estructura SKMatrix
La estructura SKMatrix define nueve propiedades de lectura y escritura de tipo float correspondientes a las nueve celdas de la matriz de transformación:
│ ScaleX SkewY Persp0 │ │ SkewX ScaleY Persp1 │ │ TransX TransY Persp2 │
SKMatrix también define una propiedad denominada Values de tipo float[]. Esta propiedad se puede usar para establecer u obtener los nueve valores de una toma en el orden ScaleX, SkewX, TransX, SkewY, ScaleY, TransY, Persp0, Persp1 y Persp2.
Las celdas Persp0, Persp1 y Persp2 se describen en el artículo Transformaciones no afines. Si estas celdas tienen sus valores predeterminados de 0, 0 y 1, la transformación se multiplica por un punto de coordenada como este:
│ ScaleX SkewY 0 │
| x y 1 | × │ SkewX ScaleY 0 │ = | x' y' z' |
│ TransX TransY 1 │
x' = ScaleX · x + SkewX · y + TransX
y' = SkewX · x + ScaleY · y + TransY
z' = 1
Esta es la transformación afín bidimensional completa. La transformación afín conserva las líneas paralelas, lo que significa que un rectángulo nunca se transforma en nada distinto de un paralelogramo.
La estructura SKMatrix define varios métodos estáticos para crear valores SKMatrix. Todos estos devuelven valores SKMatrix:
MakeTranslationMakeScaleMakeScalecon un punto dinámicoMakeRotationpara un ángulo en radianesMakeRotationpara un ángulo en radianes con un punto dinámicoMakeRotationDegreesMakeRotationDegreescon un punto dinámicoMakeSkew
SKMatrix también define varios métodos estáticos que concatenan dos matrices, lo que significa multiplicarlas. Estos métodos se denominan Concat, PostConcat y PreConcat, y hay dos versiones de cada uno. Estos métodos no tienen valores devueltos; en su lugar, hacen referencia a los valores de SKMatrix existentes a través de argumentos ref. En el ejemplo siguiente, A, B y R (para "resultado") son todos los valores de SKMatrix.
Los dos métodos Concat se llaman así:
SKMatrix.Concat(ref R, A, B);
SKMatrix.Concat(ref R, ref A, ref B);
Estos realizan la multiplicación siguiente:
R = B × A
Los otros métodos solo tienen dos parámetros. El primer parámetro se modifica y, a partir de la llamada al método, contiene el producto de las dos matrices. Los dos métodos PostConcat se llaman así:
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, ref B);
Estas llamadas realizan la siguiente operación:
A = A × B
Los dos métodos PreConcat son similares:
SKMatrix.PreConcat(ref A, B);
SKMatrix.PreConcat(ref A, ref B);
Estas llamadas realizan la siguiente operación:
A = B × A
Las versiones de estos métodos con todos los argumentos de ref son ligeramente más eficaces al llamar a las implementaciones subyacentes, pero puede resultar confuso para alguien que lea el código y suponiendo que cualquier cosa con un argumento ref se modifique mediante el método. Además, a menudo es conveniente pasar un argumento que es el resultado de uno de los métodos de Make, por ejemplo:
SKMatrix result;
SKMatrix.Concat(result, SKMatrix.MakeTranslation(100, 100),
SKMatrix.MakeScale(3, 3));
Esto crea la siguiente matriz:
│ 3 0 0 │ │ 0 3 0 │ │ 100 100 1 │
Esta es la transformación de escala multiplicada por la transformación de traducción. En este caso concreto, la estructura SKMatrix proporciona un acceso directo con un método denominado SetScaleTranslate:
SKMatrix R = new SKMatrix();
R.SetScaleTranslate(3, 3, 100, 100);
Esta es una de las pocas veces en que es seguro usar el constructor SKMatrix. El método SetScaleTranslate establece las nueve celdas de la matriz. También es seguro usar el constructor SKMatrix con los métodos estáticos Rotate y RotateDegrees:
SKMatrix R = new SKMatrix();
SKMatrix.Rotate(ref R, radians);
SKMatrix.Rotate(ref R, radians, px, py);
SKMatrix.RotateDegrees(ref R, degrees);
SKMatrix.RotateDegrees(ref R, degrees, px, py);
Estos métodos no concatenan una transformación de rotación a una transformación existente. Los métodos establecen todas las celdas de la matriz. Son funcionalmente idénticos a los métodos MakeRotation y MakeRotationDegrees, excepto que no crean instancias del valor de SKMatrix.
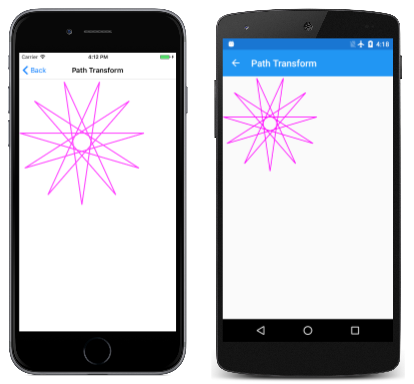
Supongamos que tiene un objeto SKPath que desea mostrar, pero prefiere que tenga una orientación algo diferente o un punto central diferente. Puede modificar todas las coordenadas de esa ruta llamando al método Transform de SKPath con un argumento SKMatrix. La página Transformación de ruta muestra cómo hacerlo. La clase PathTransform hace referencia al objeto HendecagramPath en un campo, pero usa su constructor para aplicar una transformación a esa ruta de acceso:
public class PathTransformPage : ContentPage
{
SKPath transformedPath = HendecagramArrayPage.HendecagramPath;
public PathTransformPage()
{
Title = "Path Transform";
SKCanvasView canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
SKMatrix matrix = SKMatrix.MakeScale(3, 3);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeRotationDegrees(360f / 22));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(300, 300));
transformedPath.Transform(matrix);
}
...
}
El objeto HendecagramPath tiene un centro en (0, 0) y los 11 puntos de la estrella se extienden hacia fuera desde ese centro en 100 unidades en todas las direcciones. Esto significa que la ruta tiene coordenadas positivas y negativas. La página Transformación de ruta prefiere trabajar con una estrella tres veces más grande y con todas las coordenadas positivas. Además, no quiere que un punto de la estrella apunte directamente hacia arriba. En su lugar, quiere que un punto de la estrella apunte directamente hacia abajo. (Dado que la estrella tiene 11 puntos, no puede tener ambos). Esto requiere girar la estrella en 360 grados dividido entre 22.
El constructor crea un objeto SKMatrix a partir de tres transformaciones independientes mediante el método PostConcat con el siguiente patrón, donde A, B y C son instancias de SKMatrix:
SKMatrix matrix = A;
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, C);
Se trata de una serie de multiplicaciones sucesivas, por lo que el resultado es el siguiente:
A × B × C
Las multiplicaciones consecutivas ayudan a comprender lo que hace cada transformación. La transformación de escala aumenta el tamaño de las coordenadas de ruta por un factor de 3, por lo que las coordenadas van de –300 a 300. La transformación de giro gira la estrella alrededor de su origen. Después, la transformación de traducción la desplaza por 300 píxeles hacia la derecha y hacia abajo, por lo que todas las coordenadas se convierten en positivas.
Hay otras secuencias que producen la misma matriz. Esta es otra:
SKMatrix matrix = SKMatrix.MakeRotationDegrees(360f / 22);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(100, 100));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(3, 3));
Esto gira primero la ruta de acceso alrededor de su centro y, a continuación, lo traduce a 100 píxeles a la derecha y hacia abajo, por lo que todas las coordenadas son positivas. A continuación, la estrella aumenta de tamaño en relación con su nueva esquina superior izquierda, que es el punto (0, 0).
El controlador PaintSurface simplemente puede representar esta ruta:
public class PathTransformPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Magenta;
paint.StrokeWidth = 5;
canvas.DrawPath(transformedPath, paint);
}
}
}
Aparece en la esquina superior izquierda del lienzo:
El constructor de este programa aplica la matriz a la ruta con la siguiente llamada:
transformedPath.Transform(matrix);
La ruta no conservar esta matriz como una propiedad. En su lugar, aplica la transformación a todas las coordenadas de la ruta. Si se vuelve a llamar a Transform, la transformación se vuelve a aplicar y la única manera en que puede volver es aplicando otra matriz que deshace la transformación. Afortunadamente, la estructura SKMatrix define un método TryInvert que obtiene la matriz que invierte una matriz determinada:
SKMatrix inverse;
bool success = matrix.TryInverse(out inverse);
El método se denomina TryInverse porque no todas las matrices son invertibles, pero es probable que no se use una matriz invertible para una transformación de gráficos.
También puede aplicar una transformación de matriz a un valor de SKPoint, una matriz de puntos, un SKRect o incluso un solo número dentro del programa. La estructura SKMatrix admite estas operaciones con una colección de métodos que comienzan con la palabra Map, como estas:
SKPoint transformedPoint = matrix.MapPoint(point);
SKPoint transformedPoint = matrix.MapPoint(x, y);
SKPoint[] transformedPoints = matrix.MapPoints(pointArray);
float transformedValue = matrix.MapRadius(floatValue);
SKRect transformedRect = matrix.MapRect(rect);
Si usa ese último método, tenga en cuenta que la estructura SKRect no es capaz de representar un rectángulo girado. El método solo tiene sentido para un valor de SKMatrix que representa la traducción y el escalado.
Experimentación interactiva
Una manera de entender la transformación afín es moviendo interactivamente tres esquinas de un mapa de bits alrededor de la pantalla y viendo los resultados de transformación. Esta es la idea detrás de la página de Mostrar matriz afín. Esta página requiere otras dos clases que también se usan en otras demostraciones:
La clase TouchPoint muestra un círculo translúcido que se puede arrastrar alrededor de la pantalla. TouchPoint requiere que un SKCanvasView o un elemento primario de un SKCanvasView tengan asociado el TouchEffect. Establezca la propiedad Capture en true. En el controlador de eventos TouchAction, el programa debe llamar al método ProcessTouchEvent en TouchPoint para cada instancia de TouchPoint. El método devuelve true si el evento táctil dio lugar al movimiento del punto táctil. Además, el controlador de PaintSurface debe llamar al método Paint en cada instancia de TouchPoint y pasarlo al objeto SKCanvas.
TouchPoint muestra una manera común de que un objeto visual SkiaSharp se pueda encapsular en una clase independiente. La clase puede definir propiedades para especificar características del objeto visual y un método denominado Paint con un argumento SKCanvas puede representarlo.
La propiedad Center de TouchPoint indica la ubicación del objeto. Esta propiedad se puede establecer para inicializar la ubicación; la propiedad cambia cuando el usuario arrastra el círculo alrededor del lienzo.
La página Mostrar matriz afín también requiere la clase MatrixDisplay. Esta clase muestra las celdas de un objeto SKMatrix. Tiene dos métodos públicos: Measure para obtener las dimensiones de la matriz representada y Paint para mostrarla. La clase contiene una propiedad MatrixPaint de tipo SKPaint que se puede reemplazar por un color o tamaño de fuente diferente.
El archivo ShowAffineMatrixPage.xaml crea una instancia del SKCanvasView y adjunta un TouchEffect. El archivo de código subyacente ShowAffineMatrixPage.xaml.cs crea tres objetos TouchPoint y, a continuación, los establece en posiciones correspondientes a tres esquinas de un mapa de bits que carga desde un recurso incrustado:
public partial class ShowAffineMatrixPage : ContentPage
{
SKMatrix matrix;
SKBitmap bitmap;
SKSize bitmapSize;
TouchPoint[] touchPoints = new TouchPoint[3];
MatrixDisplay matrixDisplay = new MatrixDisplay();
public ShowAffineMatrixPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
touchPoints[0] = new TouchPoint(100, 100); // upper-left corner
touchPoints[1] = new TouchPoint(bitmap.Width + 100, 100); // upper-right corner
touchPoints[2] = new TouchPoint(100, bitmap.Height + 100); // lower-left corner
bitmapSize = new SKSize(bitmap.Width, bitmap.Height);
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
}
...
}
Una matriz afín se define de forma única por tres puntos. Los tres objetos TouchPoint corresponden a las esquinas superior izquierda, superior derecha e inferior izquierda del mapa de bits. Dado que una matriz afín solo es capaz de transformar un rectángulo en un paralegrama, el cuarto punto está implícito en los otros tres. El constructor concluye con una llamada a ComputeMatrix, que calcula las celdas de un objeto SKMatrix a partir de estos tres puntos.
El controlador de TouchAction llama al método ProcessTouchEvent de cada TouchPoint. El valor de scale convierte de coordenadas de Xamarin.Forms a píxeles:
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnTouchEffectAction(object sender, TouchActionEventArgs args)
{
bool touchPointMoved = false;
foreach (TouchPoint touchPoint in touchPoints)
{
float scale = canvasView.CanvasSize.Width / (float)canvasView.Width;
SKPoint point = new SKPoint(scale * (float)args.Location.X,
scale * (float)args.Location.Y);
touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
}
if (touchPointMoved)
{
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
canvasView.InvalidateSurface();
}
}
...
}
Si TouchPoint se ha movido, el método llama a ComputeMatrix de nuevo e invalida la superficie.
El método ComputeMatrix determina la matriz implícita por esos tres puntos. La matriz denominada A transforma un rectángulo cuadrado de un píxel en un paralelismo basado en los tres puntos, mientras que la transformación de escala denominada S escala el mapa de bits a un rectángulo cuadrado de un píxel. La matriz compuesta es S × A:
public partial class ShowAffineMatrixPage : ContentPage
{
...
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.Concat(ref result, A, S);
return result;
}
...
}
Por último, el método PaintSurface representa el mapa de bits basado en esa matriz, muestra la matriz en la parte inferior de la pantalla y representa los puntos táctiles en las tres esquinas del mapa de bits:
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Display the bitmap using the matrix
canvas.Save();
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, 0, 0);
canvas.Restore();
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(matrix);
matrixDisplay.Paint(canvas, matrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Display the touchpoints
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
}
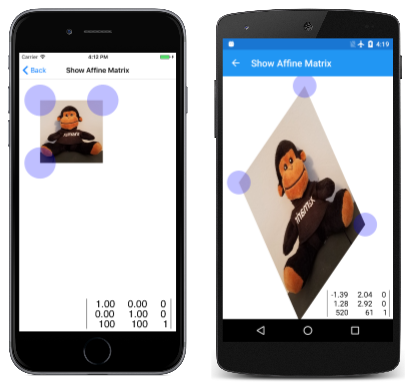
La pantalla de iOS siguiente muestra el mapa de bits cuando la página se carga por primera vez, mientras que las otras dos pantallas lo muestran después de alguna manipulación:
Aunque parece que los puntos táctiles arrastran las esquinas del mapa de bits, es solo una ilusión. La matriz calculada a partir de los puntos táctiles transforma el mapa de bits para que las esquinas coincidan con los puntos táctiles.
Es más natural que los usuarios muevan, cambien el tamaño y giren mapas de bits no arrastrando las esquinas, sino usando uno o dos dedos directamente en el objeto para arrastrar, reducir y girar. Esto se trata en el siguiente artículo Manipulación táctil.
La razón de la matriz 3 a 3
Es posible que se espere que un sistema de gráficos bidimensionales requiera solo una matriz de transformación de 2 a 2:
│ ScaleX SkewY │
| x y | × │ │ = | x' y' |
│ SkewX ScaleY │
Esto funciona para escalar, rotar e incluso escalonar, pero no es capaz de las transformaciones más básicas, que es la traducción.
El problema es que la matriz de 2 a 2 representa una transformación lineal en dos dimensiones. Una transformación lineal conserva algunas operaciones aritméticas básicas, pero una de las implicaciones es que una transformación lineal nunca modifica el punto (0, 0). Una transformación lineal hace que la traducción sea imposible.
En tres dimensiones, una matriz de transformación lineal tiene este aspecto:
│ ScaleX SkewYX SkewZX │
| x y z | × │ SkewXY ScaleY SkewZY │ = | x' y' z' |
│ SkewXZ SkewYZ ScaleZ │
La celda etiquetada SkewXY significa que el valor sesga la coordenada X en función de los valores de Y; la celda SkewXZ significa que el valor sesga la coordenada X en función de los valores de Z; y los valores sesgarán de forma similar para las demás celdas de Skew.
Es posible restringir esta matriz de transformación 3D a un plano bidimensional estableciendo SkewZX y SkewZY en 0 y ScaleZ a 1:
│ ScaleX SkewYX 0 │
| x y z | × │ SkewXY ScaleY 0 │ = | x' y' z' |
│ SkewXZ SkewYZ 1 │
Si los gráficos bidimensionales se dibujan completamente en el plano en el espacio 3D donde Z es igual a 1, la multiplicación de transformación tiene este aspecto:
│ ScaleX SkewYX 0 │
| x y 1 | × │ SkewXY ScaleY 0 │ = | x' y' 1 |
│ SkewXZ SkewYZ 1 │
Todo permanece en el plano bidimensional donde Z es igual a 1, pero las celdas SkewXZ y SkewYZ se convierten efectivamente en factores de traducción bidimensional.
Así es como una transformación lineal tridimensional actúa como una transformación no lineal bidimensional. (Por analogía, las transformaciones en gráficos 3D se basan en una matriz de 4 a 4).
La estructura SKMatrix de SkiaSharp define las propiedades de esa tercera fila:
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z` |
│ TransX TransY Persp2 │
Los valores no cero de Persp0 y Persp1 dan lugar a transformaciones que mueven objetos fuera del plano bidimensional donde Z es igual a 1. Lo que sucede cuando esos objetos se mueven de nuevo a ese plano se tratan en el artículo sobre Transformaciones no afines.